①$(N_1)_r\Rightarrow 十进制target$

②$(N_2)_?=target$

初步的想法：枚举进制，假设最终答案的进制为x，则$(N_2)_x=target$，那么接下来要确定x的范围

x的最小值为$N_2$中所有数字的最大值加 + 1，这很容易理解，因为一个数字的各个位上的数都不会超过它的进制，如：123 最小进制为4，进制>= 最大数+1 = 3 + 1 = 4

x的最大值要分析一下，分析如下：

$(N_1)$的最大位数为10位，最大进制为36进制，所以转成十进制的最大数为$36^{10}$

例：$(10)_b=1\times b^1 + 0\times b^0 = b$，所以$N_2$的最大进制可以是$36^{10}$，所以x的最大值为target + 1（为什么不是target最后有说明）

很显然，枚举区间很大，当枚举区间很大时，我们会想，能不能用二分来求？

当进制变大时，数也一定是单调不减的（为什么不是单调递增，而是单调不减，后面有说明），所以可以用二分。二分的左端点为$N_2$中所有数字的最大值加 + 1，右端点为$36^{10}$。我们找的是大于等于答案的最小进制数，所以用这个模板：

int l = 0,r = n - 1;
//找左边界
while(l < r){
    int mid = l + r >> 1;
    if(a[mid] >= x){
        r = mid;
    }else{
        l = mid + 1;
    }
}

题干描述，如果答案不唯一，则输出更小的进制数：这种情况是target为一位数的时候，如十进制6，等于≥7的进制的6。如$(6)_7 = (6)_8 = (6)_9 = (6)_{10} = (6)_{11} = …$，因此当进制变大时，数也一定是单调不减的

秦九昭算法计算多项式的值：

def calc(s, val):# 利用秦九昭算法计算多项式的值，s为多项式，val为上图中的x值
    res = 0
    for c in s: 
        res = res * val + get(c)
    return res

本题完整代码如下：

def get(c):# 将字符'0'~'9'转成数字0 ~ 9，将字符 'a' ∼ 'z'转成数字 10∼35
    oc = ord(c)
    if oc <= ord('9'): 
        return oc - ord('0')
    return oc - ord('a') + 10

def calc(s, val):# 利用秦九昭算法计算多项式的值
    res = 0
    for c in s: 
        res = res * val + get(c)
    return res

n1, n2, tag, radix = input().split()
if tag == '2': 
    # 统一化，N1 N2 tag radix，4个变量中，默认N1是已知的radix进制数，N2是未知的进制数，通过交换实现
    n1, n2 = n2, n1

target = calc(n1, int(radix))

l, r = 0, 36 ** 10
for x in n2: 
    l = max(l, get(x) + 1)  # 进制最小值为n2中所有数字的最大值加+1

# 二分找大于等于答案的最小进制数    
while l < r:
    mid = l + r >> 1
    if (calc(n2, mid) >= target): 
        r = mid
    else: 
        l = mid + 1
if calc(n2, r) != target: 
    print("Impossible")
else: 
    print(r)

上面的代码是直接将r取成$36^{10}$了，还可以将进制右边界r取成target + 1进一步来优化一下：

l, r = 0, target + 1
for x in n2: 
    l = max(l, get(x) + 1)  # 进制最小值为n2中所有数字的最大值加+1

为什么要+1？

因为有如下的特例：

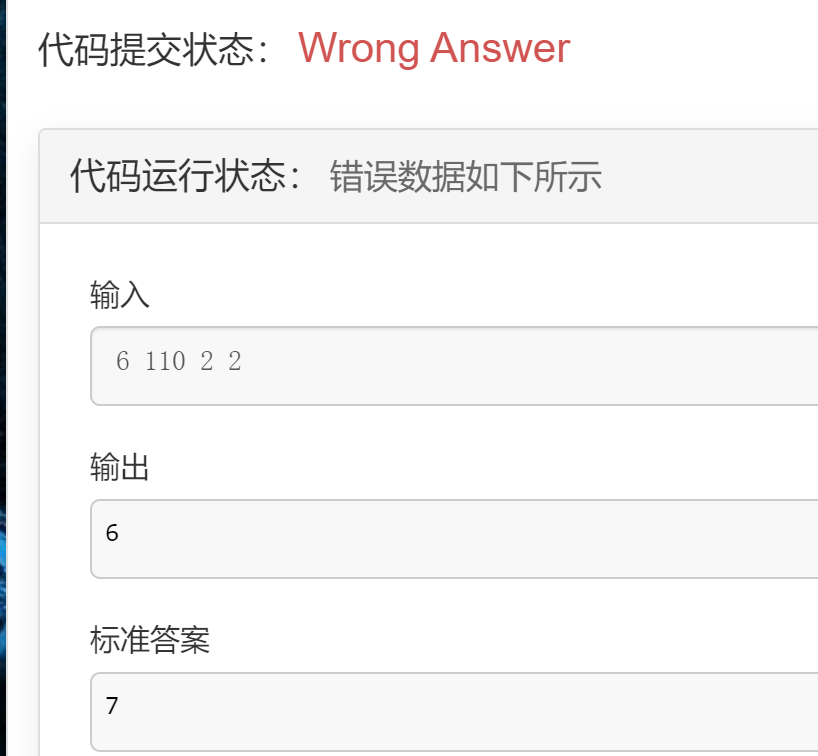
此时l为7，target为6，即r取成6了，所以一开始l < r这个条件都不满足，都没进行二分

因此进制的最大数为target + 1