基础算法

常用代码模板1——基础算法

排序算法

1 快速排序

#include<iostream>
#include<cstdio>
using namespace std;

const int M=1e5+10;
int a[M];
int n;

void q_sort(int l,int r){
    if(l>=r) return;
    int i=l-1,j=r+1,x=a[(l+r)/2];
    while(i<j){
        do i++;while(x>a[i]);
        do j--;while(x<a[j]);
        if(i<j) swap(a[i],a[j]);
    }
    q_sort(l,j),q_sort(j+1,r);//此处边界不能换为(l,i),(i+1,r) 否则会死循环
}

// 另一种写法 边界不同
// void q_sort(int l,int r){
//     if(l>=r) return;
//     int i=l-1,j=r+1,x=a[(l+r+1)/2]; ***
//     while(i<j){
//         do i++;while(x>a[i]);
//         do j--;while(x<a[j]);
//         if(i<j) swap(a[i],a[j]);
//     }
//     q_sort(l,i-1),q_sort(i,r); ***
// }

int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;i++) scanf("%d",&a[i]);
    q_sort(1,n);
    for(int i=1;i<=n;i++) printf("%d ",a[i]);
    return 0;
}

2 归并排序

#include<iostream>
#include<cstdio>
using namespace std;

const int M=1e5+10;
int a[M],b[M];
int n;

void merge_sort(int l,int r){
    if(l>=r) return;
    int mid=l+r>>1;
    merge_sort(l,mid),merge_sort(mid+1,r);
    int i=l,j=mid+1,k=l;
    while(i<=mid && j<=r)
        if(a[i]<a[j])
            b[k++]=a[i++];
        else b[k++]=a[j++];
    while(i<=mid) b[k++]=a[i++];
    while(j<=r) b[k++]=a[j++];
    for(int i=l;i<=r;i++) a[i]=b[i];
}

int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;i++) scanf("%d",&a[i]);
    merge_sort(1,n);
    for(int i=1;i<=n;i++) printf("%d ",a[i]);
    return 0;
}

二分

整数二分算法模板

bool check(int x) {/* ... */} // 检查x是否满足某种性质

1 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用

// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用：
int bsearch_1(int l, int r)
{
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;    // check()判断mid是否满足性质
        else l = mid + 1;
    }
    return l;
}

2 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用

// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用：
int bsearch_2(int l, int r)
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

3 浮点数二分算法模板

// 浮点数二分算法模板

bool check(double x) {/* ... */} // 检查x是否满足某种性质

double bsearch_3(double l, double r)
{
    const double eps = 1e-6;   // eps 表示精度，取决于题目对精度的要求
    while (r - l > eps)
    {
        double mid = (l + r) / 2;
        if (check(mid)) r = mid;
        else l = mid;
    }
    return l;
}

高精度

1 加法

t+=a[i]+b[i]; c.push_back(t%10); t/=10

#include<iostream>
#include<cstdio>
#include<cstring>
#include<vector>
using namespace std;

vector<int> add(vector<int> &a,vector<int> &b){
    vector<int> c;
    int t=0;//进位
    for(int i=0;i<a.size() || i<b.size();i++){
        if(i<a.size()) t+=a[i];
        if(i<b.size()) t+=b[i];
        c.push_back(t%10);
        t/=10;//进位权重下降
    }
    if(t) c.push_back(1);
    return c;
}

int main(){
    vector<int> a,b;
    string A,B;
    cin>>A>>B;
    for(int i=A.size()-1;i>=0;i--) a.push_back(A[i]-'0');
    for(int i=B.size()-1;i>=0;i--) b.push_back(B[i]-'0');
    vector<int> c=add(a,b);
    for(int i=c.size()-1;i>=0;i--) printf("%d",c[i]);
    return 0;
}

2 减法

利用cmp()比较大小

t=a[i]-t;t-=b[i];if(t<0) t=1;else t=0

#include<iostream>
#include<cstdio>
#include<cstring>
#include<vector>
using namespace std;

bool cmp(vector<int> &a,vector<int> &b){
    if(a.size()!=b.size()) return a.size()>b.size();
    for(int i=a.size();i>=0;i--)
        if(a[i]!=b[i])
            return a[i]>b[i];
    return true;
}

vector<int> sub(vector<int> &a,vector<int> &b){
    vector<int> c;
    int t=0;//借位
    for(int i=0;i<a.size();i++){
        t=a[i]-t;
        if(i<b.size()) t-=b[i];
        c.push_back((t+10)%10);
        if(t<0) t=1;//t<0 表示借位了
        else t=0;//否则就是没借位
    }
    while(c.size()>1 && c.back()==0) c.pop_back();
    return c;
}

int main(){
    vector<int> a,b;
    string A,B;
    cin>>A>>B;
    for(int i=A.size()-1;i>=0;i--) a.push_back(A[i]-'0');
    for(int i=B.size()-1;i>=0;i--) b.push_back(B[i]-'0');
    if(cmp(a,b)){
        vector<int> c=sub(a,b);
        for(int i=c.size()-1;i>=0;i--) printf("%d",c[i]);
    }else{
        vector<int> c=sub(b,a);
        printf("-");
        for(int i=c.size()-1;i>=0;i--) printf("%d",c[i]);
    }
    return 0;
}

3 乘法

t+=a[i]*b;c.push_back(t%10);t/=10

// 高精乘低精
#include<iostream>
#include<cstdio>
#include<cstring>
#include<vector>
using namespace std;

vector<int> mul(vector<int> &a,int &b){
    vector<int> c;
    for(int i=0,t=0;i<a.size() || t;i++){//进位存在或没乘完
        if(i<a.size()) t+=a[i]*b;
        c.push_back(t%10);
        t/=10;
    }
    while(c.size()>1 && c.back()==0) c.pop_back();//去除前导零
    return c;
}

int main(){
    vector<int> a;
    int b;
    string A;
    cin>>A>>b;
    for(int i=A.size()-1;i>=0;i--) a.push_back(A[i]-'0');
    vector<int> c=mul(a,b);
    for(int i=c.size()-1;i>=0;i--) printf("%d",c[i]);
    return 0;
}

// 高精乘高精
#include <iostream>
#include <cstring>
#include <vector>

using namespace std;

string A, B;
vector<int> a, b;

vector<int> mul(vector<int> &a, vector<int> &b) {
    vector<int> c;
    c.resize(a.size() + b.size());
    for (int i = 0; i < a.size(); ++ i) {
        int t = 0;
        for (int j = 0; j < b.size(); ++ j) {
            c[i + j] += t + a[i] * b[j];
            t = c[i + j] / 10;
            c[i + j] %= 10;
        }
        c[i + b.size()] = t;
    }
    while (c.size() > 1 && c.back() == 0) c.pop_back();
    return c;
}

int main() {
    cin >> A >> B;
    for (int i = A.size() - 1; i >= 0; -- i) a.push_back(A[i] - '0');
    for (int i = B.size() - 1; i >= 0; -- i) b.push_back(B[i] - '0');
    vector<int> c = mul(a, b);
    for (int i = c.size() - 1; i >= 0; -- i) cout << c[i];
    cout << endl;
    return 0;
}

4 除法

r=r*10+a[i];c.push_back(r/b);r%=b

// 高精除低精
#include<iostream>
#include<cstdio>
#include<cstring>
#include<vector>
#include<algorithm>
using namespace std;

vector<int> div(vector<int> &a,int &b,int &r){
    vector<int> c;
    r=0;
    for(int i=a.size()-1;i>=0;i--){
        r=r*10+a[i];
        c.push_back(r/b);
        r%=b;
    }
    reverse(c.begin(),c.end());
    while(c.size()>1 && c.back()==0) c.pop_back();//去除前导零
    return c;
}

int main(){
    vector<int> a;
    int b,r;
    string A;
    cin>>A>>b;
    for(int i=A.size()-1;i>=0;i--) a.push_back(A[i]-'0');
    vector<int> c=div(a,b,r);
    for(int i=c.size()-1;i>=0;i--) printf("%d",c[i]);
    printf("\n%d",r);
    return 0;
}

// 高精除高精
#include<cstdio>
#include<cstring>

using namespace std;

const int MAXN=300+4; //根据题目的最大值。+4为了防止A+B出现进位
char s1[MAXN];//存储字符串
char s2[MAXN];//存储字符串
int tmp[MAXN];//交换用字符串
int a[MAXN];//存储加数A
int b[MAXN];//存储加数B
int c[MAXN];//存储和B

int compare(int a[], int b[]) {
    //索引为0的数据为数组长度
    if (a[0]>b[0]) {
        return 1;
    } else if (a[0]<b[0]) {
        return -1;
    }

    //逐位比较
    for (int i=a[0]; i>0; i--) {
        if (a[i]>b[i]) {
            return 1;
        } else if (a[i]<b[i]) {
            return -1;
        }
    }

    return 0;
}

void numcpy(int a[],int b[],int dest) {
    //将数组右移，使两个数组右端对齐，形参b数组储存右移后的结果
    for (int i=1;i<=a[0];i++) {
        b[i+dest-1] =a[i];
    }
    b[0] = a[0]+dest-1;
}

int main() {
    scanf("%s %s", s1, s2);//读入字符串

    //处理数1
    int len = strlen(s1);
    a[0] = len;
    for (int i=0; i<len; i++) {
        a[len-i]=s1[i]-'0';
    }

    //处理数2
    len = strlen(s2);
    b[0] = len;
    for (int i=0; i<len; i++) {
        b[len-i]=s2[i]-'0';
    }

    if (0==compare(a,b)) {
        //两数相等
        printf("1\n0\n");
        return 0;
    } else if (-1==compare(a,b)) {
        //被除数小，除数大
        printf("0\n");//输出除数
        printf("%s\n", s1);
        return 0;
    } else {
        c[0] = a[0]-b[0]+1;
        for (int i=c[0]; i>0; i--) {
            memset(tmp, 0, sizeof(tmp));
            //高位对齐
            numcpy(b,tmp,i);

            //
            while (compare(a, tmp)>=0) {
                c[i]++;
                //减法
                for (int j=1; j<=a[0]; j++) {
                    if (a[j]<tmp[j]) {
                        a[j+1]--;
                        a[j]+=10;
                    }
                    a[j]-=tmp[j];
                }

                int k=a[0];
                while (a[k]==0) {
                    k--;
                }
                a[0]=k;
            }
        }

        //控制最高位的0
        while (c[0]>0 && c[c[0]]==0) {
            c[0]--;
        }
    }

    //逆序打印输出商和余数
    for (int i=c[0]; i>0; i--) {
        printf("%d", c[i]);
    }
    printf("\n");
    if (0==a[0]) {
        printf("0\n");
    } else {
        for (int i=a[0]; i>0; i--) {
            printf("%d", a[i]);
        }
        printf("\n");
    }

    return 0;
}

前缀和差分

1 一维前缀和

S[i] = a[1] + a[2] + ... a[i]

a[l] + ... + a[r] = S[r] - S[l - 1]

#include<iostream>
#include<cstdio>
using namespace std;
const int M=1e5+10;
int a[M],b[M];
int main(){
    int n,m;
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) scanf("%d",&a[i]);
    for(int i=1;i<=n;i++) b[i]=a[i]+b[i-1];
    while(m--){
        int l,r;
        scanf("%d%d",&l,&r);
        printf("%d\n",b[r]-b[l-1]);
    }
}

2二维前缀和

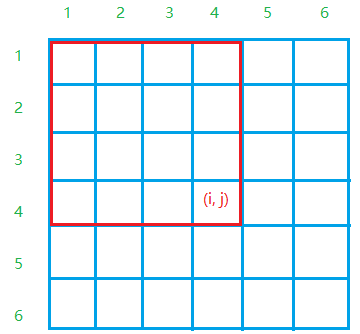
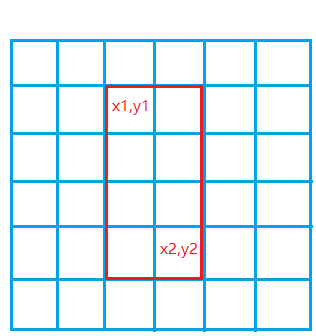
1.S[i,j]即为图1红框中所有数的的和为：

S[i,j]=S[i,j−1]+S[i−1,j]−S[i−1,j−1]+a[i,j]

2.(x1,y1),(x2,y2)(x1,y1),(x2,y2)这一子矩阵中的所有数之和为：

S[x2,y2]−S[x1−1,y2]−S[x2,y1−1]+S[x1−1,y1−1]

#include<iostream>
#include<cstdio>
using namespace std;

const int M=1e3+10;
int a[M][M],b[M][M];
int n,m,q,x1,y1,x2,y2;

int main(){
    scanf("%d%d%d",&n,&m,&q);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            scanf("%d",&a[i][j]);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            b[i][j]=b[i-1][j]+b[i][j-1]-b[i-1][j-1]+a[i][j];
    while(q--){
        scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
        printf("%d\n",b[x2][y2]-b[x1-1][y2]-b[x2][y1-1]+b[x1-1][y1-1]);
    }
}

3一维差分

构造差分数组 B[i] = a[i] - a[i - 1]

给区间[l, r]中的每个数加上c：B[l] += c, B[r + 1] -= c

差分是前缀和的逆运算，即 差分数组的前缀和是原数组

#include<iostream>
#include<cstdio>
using namespace std;

const int M=1e5+10;
int a[M],b[M];
int n,m;
int l,r,c;

void in(int l,int r,int c){//插入
    b[l]+=c;
    b[r+1]-=c;
}

int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) scanf("%d",&a[i]);
    for(int i=1;i<=n;i++) b[i]=a[i]-a[i-1];//构造差分数组
    for(int i=1;i<=m;i++){
        scanf("%d%d%d",&l,&r,&c);
        in(l,r,c);
    }
    for(int i=1;i<=n;i++) b[i]=b[i]+b[i-1];//还原数组
    for(int i=1;i<=n;i++) printf("%d ",b[i]);
}   

4二维差分

给以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵中的所有元素加上c：
S[x1, y1] += c, S[x2 + 1, y1] -= c, S[x1, y2 + 1] -= c, S[x2 + 1, y2 + 1] += c

#include<iostream>
#include<cstdio>

using namespace std;

const int M=1000+10;
int n,m,q;
int a[M][M],s[M][M];
int x1,y1,x2,y2,c;

void in(int x1,int y1,int x2,int y2,int c){//插入
    s[x1][y1]+=c;
    s[x2+1][y1]-=c;
    s[x1][y2+1]-=c;
    s[x2+1][y2+1]+=c;
}

int main(){
    scanf("%d%d%d",&n,&m,&q);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            scanf("%d",&a[i][j]);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            in(i,j,i,j,a[i][j]);//构造
    for(int i=1;i<=q;i++){
        scanf("%d%d%d%d%d",&x1,&y1,&x2,&y2,&c);
        in(x1,y1,x2,y2,c);
    }
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            s[i][j]+=s[i-1][j]+s[i][j-1]-s[i-1][j-1];//还原
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++){
            printf("%d ",s[i][j]);
            if(j==m) puts("");
        }
}

双指针算法

for (int i = 0, j = 0; i < n; i ++ )
{
    while (j < i && check(i, j)) j ++ ;

    // 具体问题的逻辑
}

常见问题分类：
(1) 对于一个序列，用两个指针维护一段区间
(2) 对于两个序列，维护某种次序，比如归并排序中合并两个有序序列的操作

位运算

求n的第k位数字:n >> k & 1
返回n的最后一位1：lowbit(n) = n & -n

离散化

vector<int> alls; 存储所有待离散化的值
sort(alls.begin(), alls.end()); 将所有值排序
alls.erase(unique(alls.begin(), alls.end()), alls.end()); 去掉重复元素

// 二分求出x对应的离散化的值
int find(int x)
{
    int l = 0, r = alls.size() - 1;
    while (l < r)
    {
        int mid = l + r >> 1;
        if (alls[mid] >= x) r = mid;
        else l = mid + 1;
    }
    return r + 1;//映射到1，2，3，...,n
}

区间合并

// 将所有存在交集的区间合并
    void merge(vector<PII> &segs)
    {
        vector<PII> res;

        sort(segs.begin(), segs.end());

        int st = -2e9, ed = -2e9;
        for (auto seg : segs)
            if (ed < seg.first)
            {
                if (st != -2e9) res.push_back({st, ed});
                st = seg.first, ed = seg.second;
            }
            else ed = max(ed, seg.second);

        if (st != -2e9) res.push_back({st, ed});

        segs = res;
    }

快速幂

#include <iostream> //快速乘方
#include <cmath>
#include <cstdio>

using namespace std;

int main()
{
    long long a, b, ans = 1, k;
    cin >> a >> b >> k;
    int y = b;
    printf("%d^%d mod %d=", a, b ,k);
    while (b)
    {
        if (b & 1) ans = ans * a % k;
        a = a * a % k;
        b >>= 1;
    }
    if (k == 1) ans = 0;
    cout << ans;
    system("pause");
}

文件读写

#include <cstdlib>
freopen("P2058_2.in", "r", stdin);
freopen("my_ans.out", "w", stdout);
fclose(stdin);
fclose(stdout);

快速读入

template<typename T>void read(T &x) {
    char ch = getchar(); bool flag = 0; x = 0;
    while (ch < '0' || ch > '9') flag |= (ch == '-'), ch = getchar();
    while (ch <= '9' && ch >= '0') x = (x << 1) + (x << 3) + ch - '0', ch = getchar();
    if (flag) x = -x; return;
}

cin加速

#define MADE_IN_HEVEAN cin.tie(0)->sync_with_stdio(0), cout.tie(0)