1.求最长上升子序列

遍历每一个元素，寻找以它为末尾元素能构成的递增子序列的长度最大值

方法：维护一个记录长度1到k的所有子序列的末尾最小值

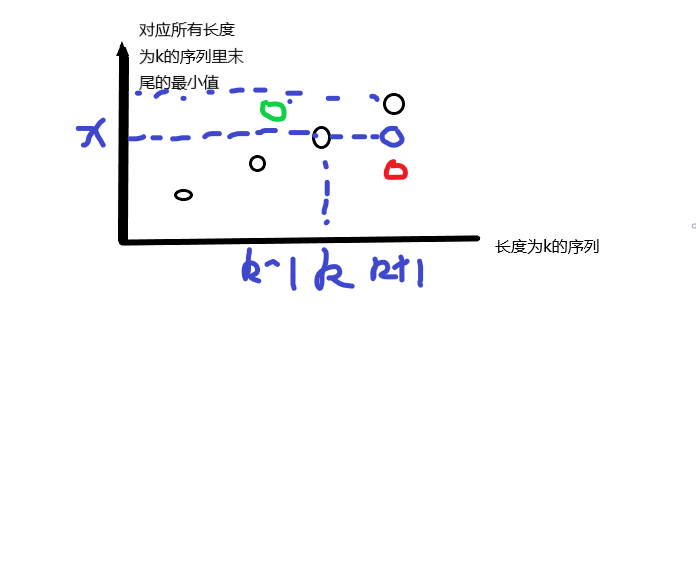
贪心的思想：若x想构成长度为k的递增序列，则必须要大于长度为k-1的序列中末尾元素的最小值

 #include <iostream>
#include <algorithm>

using namespace std;

const int N =1e5+10;

int n,q[N],a[N];

int main(){

    cin>>n;

    for(int i=0;i<n;i++) scanf("%d ",&a[i]);

    int len=0;//目前可以构成的递增子序列的最大值
    for(int i=0;i<n;i++){//二分寻找小于x的最大值
        int l=0,r=len;
        while(l<r){
            int mid=(l+r+1)>>1;
            if(q[mid]<a[i]) l=mid;
            else r=mid-1;
        }
        q[r+1]=a[i]; //r是小于x的最大值 更新r+1
        len=max(len,r+1);
    }

    cout<<len<<endl;


    return 0;
}

正确性证明：

1. 为何可以使用二分寻找k-1对应的最小值（为何队列是单调递增的）：
   如图，若k+1对应的最小值小于或等于k对应的最小值，则长度为k的序列对应的最小值也可以更新为k+1对应的最小值

2. 为什么x只能更新比x大的第一个元素
   不能更新比其更小的元素，构成的所有序列中，最小值肯定不是x
   可以使对应的长度k+1的序列的最小值更小，但是无法形成长度k+2的序列

2 最长公共子序列

方法：动态规划

闫氏dp法：
状态表示：第一个序列的前i位与第二个序列的前j位构成的最长公共子序列
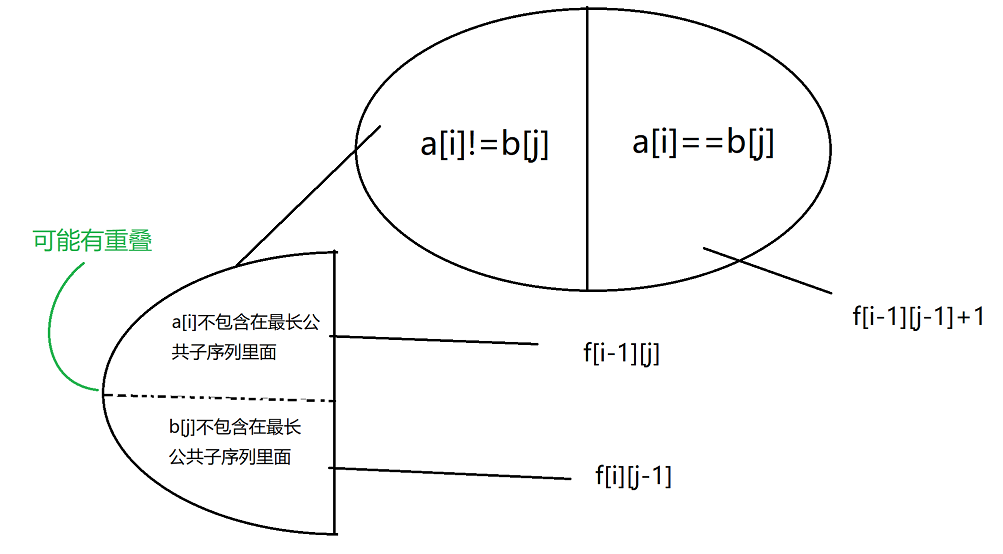
状态转移：可以将集合分为a【i】==b【j】的情况和a【i】！=b【j】的两种情况

1. a[i]==b[j] 直接f[i][j]=f[i-1][j-1]+1
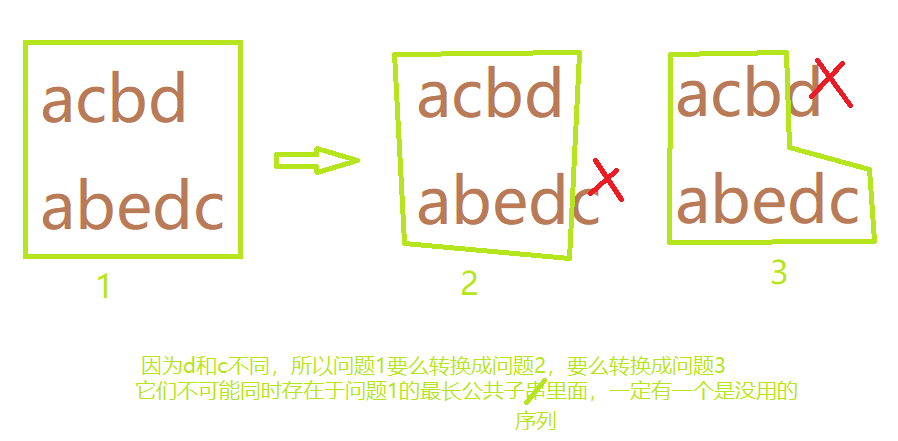
2. a[i]!=b[j] 可以继续把集合分为 a[i]不在公共子序列之中 b[j]不在公共子序列之中 a[i]b[j]都不在公共子序列之中
   它们分别对应f[i-1][j] f[i][j-1] f[i-1][j-1] 其中最后一项一定小于前两项可以省略，在前两项中找最大值
   这里引用 @yuechen大佬的两张图
   
   

#include <iostream>
using namespace std;
const int N = 1010;
int n, m;
char a[N], b[N];
int f[N][N];
int main() {
  cin >> n >> m >> a + 1 >> b + 1;
  for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= m; j++) {
      if (a[i] == b[j]) {
        f[i][j] = f[i - 1][j - 1] + 1;
      } else {
        f[i][j] = max(f[i - 1][j], f[i][j - 1]);
        //f[i][j]=max(f[i][j],f[i-1][j-1]);
      }
    }
  }
  cout << f[n][m] << '\n';
  return 0;
}

3 两者之间的转化

若在两条序列中存在一条序列a不存在重复元素，可以寻找 另一个序列b对应元素在a中位置形成的序列b 的最大上升子序列来寻找a与b之间的最长公共序列
b数组记录b中每一个元素在a中的位置
这里借用yxc大佬的一张图来表示

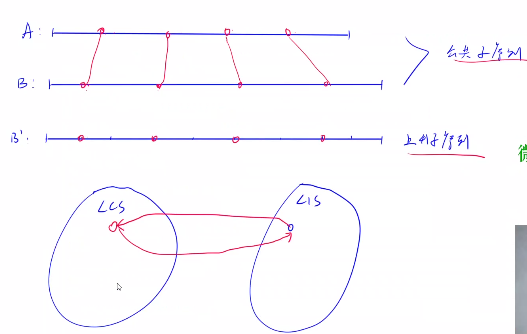
b*的每一个上升子序列都可以对应一个a与b之间的公共子序列（若不上升，则会出现对应元素前后位置不同的情况 （在b中元素已经按一定的相对顺序排列，在a中也必须是这个相对顺序，才能构成公共子序列）），反之亦然，可以推得lis和lcs两个集合是一一对应的

这时就可以对b*数组求最长上升子序列即可

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1000010;

int n;
int id[N], q[N];

int main()
{
    scanf("%d", &n);
    memset(id, -1, sizeof id);
    for (int i = 0; i < n; i ++ )
    {
        int x;
        scanf("%d", &x);
        id[x] = i;
    }

    int tt = 0;
    q[0] = -1;
    for (int i = 0; i < n; i ++ )
    {
        int x;
        scanf("%d", &x);
        int k = id[x];
        if (k == -1) continue;
        int l = 0, r = tt;
        while (l < r)
        {
            int mid = l + r + 1 >> 1;
            if (q[mid] < k) l = mid;
            else r = mid - 1;
        }
        q[r + 1] = k;
        tt = max(tt, r + 1);
    }

    printf("%d\n", tt);
    return 0;
}