AtCoder Beginner Contest 220 个人题解

比赛链接：AtCoder Beginner Contest 220

今天更新了桌面！好耶！

A题 Find Multiple

题目大意：

找 $a$ 到 $b$ 中 $c$ 的倍数并输出

思路解析：

枚举

AC代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> pii;

const int maxn=1e5+5;

int main(){

    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);

    int a,b,c;
    cin>>a>>b>>c;

    for(int i=a;i<=b;i++){
        if(i%c==0){
            cout<<i<<endl;
            return 0;
        }
    }
    cout<<-1<<endl;
}

B题 Base K

题目大意：

给出k进制的两个数，输出两个数十进制的乘积

思路解析：

模拟

AC代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> pii;

const int maxn=1e5+5;

int main(){

    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);

    ll k,a,b;
    cin>>k>>a>>b;

    ll base=1,sum=0;

    while(a){
        sum+=a%10*base;
        a/=10;
        base*=k;
    }

    ll ans=sum;
    base=1,sum=0;

    while(b){
        sum+=b%10*base;
        b/=10;
        base*=k;
    }

    cout<<sum*ans<<endl;

}

C题 Long Sequence

题目大意：

给你一个近乎无限循环的数组，输出前缀和大于X的位置

思路解析：

模拟

AC代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> pii;

const int maxn=1e5+5;

ll a[maxn];
ll sum;

int main(){

    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);

    ll n;
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>a[i];
        sum+=a[i];
    }

    ll x;
    cin>>x;

    ll ans=x/sum*n;
    x%=sum;

        ll tot=0;
        for(int i=1;i<=n;i++){
            tot+=a[i];
            if(tot>x){
                cout<<ans+i<<endl;
                break;
            }
        }

}

D题 FG operation

题目大意：

给你一个序列，有两种操作

• $F$ 操作：将最左边的两个元素 $x，y$ 删除，并用 $(x+y)\%10$ 替换
• $G$ 操作：将最左边的两个元素 $x，y$ 删除，并用 $(x*y)\%10$ 替换

$9$ 行分别输出结果分别只剩 $0-9$ 的方案数

思路解析：

傻逼$DP$

AC代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> pii;

const int maxn=1e5+5;
const int mod=998244353;

int a[maxn],n,dp[maxn][15];

int main(){

    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);

    cin>>n;

    for(int i=1;i<=n;i++)cin>>a[i];

    dp[1][a[1]]=1;

    for(int i=2;i<=n;i++){
        for(int j=0;j<=9;j++){

            dp[i][(j+a[i])%10]+=dp[i-1][j];
            dp[i][(j+a[i])%10]%=mod;
            dp[i][(j*a[i])%10]+=dp[i-1][j]%mod;
            dp[i][(j*a[i])%10]%=mod;

        }
    }

    for(int i=0;i<=9;i++)cout<<dp[n][i]<<endl;

}

E题 Distance on Large Perfect Binary Tree

题目大意：

给出一个 $2^n-1$ 个节点的完全二叉树，输出树中距离为 $d$ 的点对数量

思路解析：

我们自上而下得考虑每一个点

我们对于每一个点考虑它的两种情况：

• 情况一：经过此点距离为d的路径以这个点为端点，全部在他的左子树或者右子树上

• 情况二：经过此点距离为d的路径被这个点分成两段，分别在左右子树上

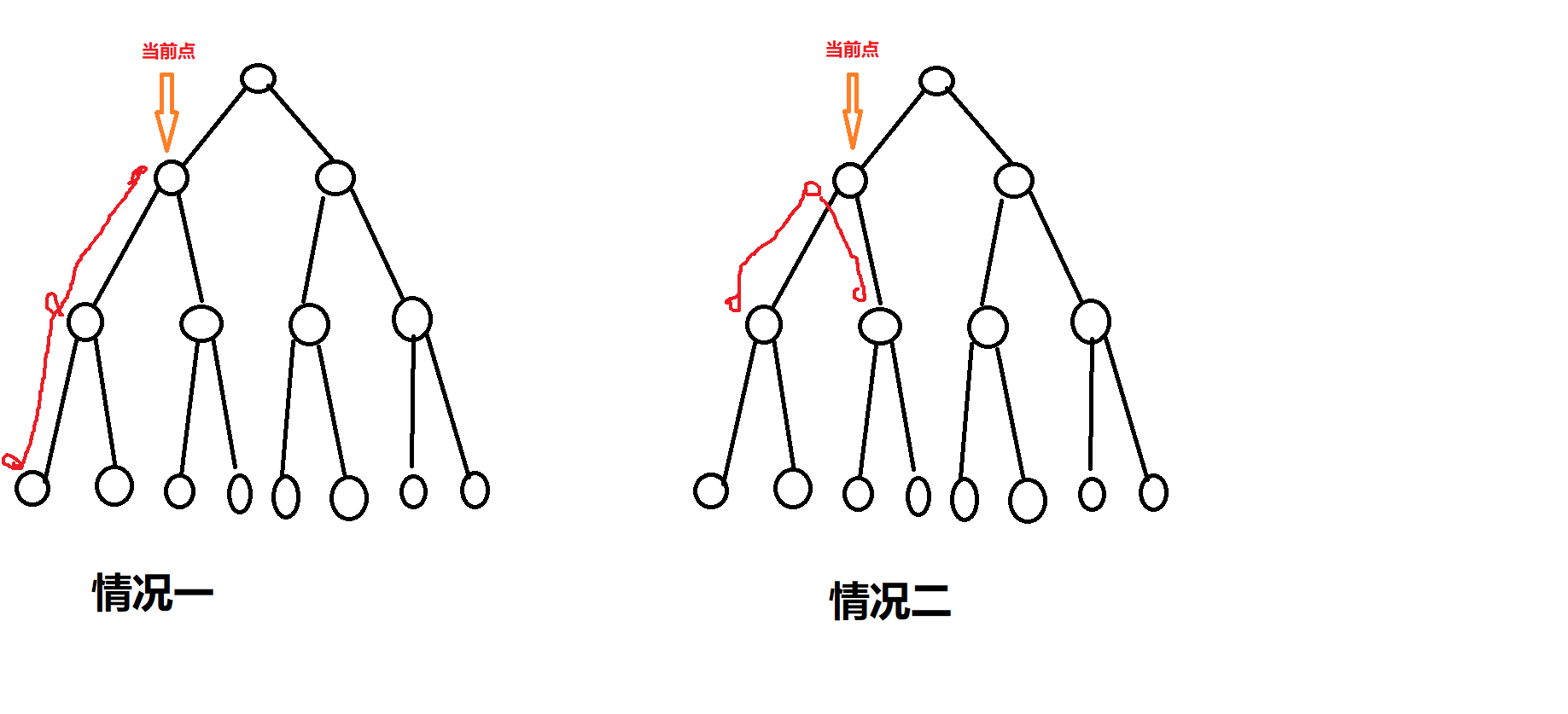
对于情况一，如果路径合法，我们就可以算出这个点的贡献为$2^d$
对于情况二，如果路径合法，我们在左右子树至少有 $1$ 长度的路径，我们设左子树的路径长度为 $l$ ，那么右子树的长度为$d-l$，我们就可以计算贡献为$(l-r+1)\*2^l-1\*2^r-1$化简之后为$(l-r+1)\*2^d-2$

每个点的贡献就是两种情况的和，而对于每一层的点来说吗，他们的贡献是一样的，所以我们只需要 $O(n)$ 的时间来枚举每一层，用 $O(1)$ 的时间计算每一层的贡献即可

AC代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> pii;

const int maxn=2e6+5;
const int mod=998244353;

ll p[maxn],ans;

int main(){

    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);

    ll n,d;
    cin>>n>>d;

    p[0]=1;

    for(int i=1;i<=maxn-3;i++)p[i]=2*p[i-1]%mod;

    for(int i=1;i<=n;i++){
        if(n-i>=d)ans=(ans+p[d]*p[i-1]%mod)%mod;
        ll l=min(d-1,n-i);
        ll r=d-l;
        if(r>n-i)continue;
        ans=(ans+(l-r+1)*p[d-2]%mod*p[i-1]%mod)%mod;
    }

    cout<<(2*ans)%mod<<endl;

}

F题 Distance Sums 2

题目大意：

给出一棵 $n$ 个节点的树，输出 $n$ 行，对于每个节点，输出以这个节点为根节点到其他所有节点的距离和

思路解析：

树形 $DP$

ans[i]表示以 $i$ 节点为根节点到其他节点的距离和，sz[i]表示每个节点的子树大小

首先我们 $DFS$ 得到ans[1],然后我们可以发现如果我们知道了一个节点的ans[],那么我们可以 $O(1)$ 转移这个节点的相邻节点

我们设当前已知答案的节点为 $fa$ ，相邻节点为 $x$ ，可以得到以下方程：

$ans[x]=ans[fa]-2*sz[x]+n$

AC代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> pii;

const int maxn=1e6+5;

int e[maxn],h[maxn],nex[maxn],id;
int n,sz[maxn];
ll ans[maxn],tmp;

void add(int x,int y){
    e[++id]=y;
    nex[id]=h[x];
    h[x]=id;
}

void dfs(int x,int fa){
    for(int i=h[x];i;i=nex[i]){
        int j=e[i];
        if(j==fa)continue;
        dfs(j,x);
        sz[x]+=sz[j];
    }
    if(x!=1)tmp+=sz[x];
}

void solve(int x,int fa){
    if(x!=1)ans[x]=ans[fa]-2*sz[x]+n;
    for(int i=h[x];i;i=nex[i]){
        int j=e[i];
        if(j==fa)continue;
        solve(j,x);
    }
}

int main(){

    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);

    cin>>n;

    for(int i=1;i<=n;i++)sz[i]=1;

    for(int i=1;i<n;i++){
        int x,y;
        cin>>x>>y;
        add(x,y);
        add(y,x);
    }

    dfs(1,1);

    ans[1]=tmp;

    solve(1,1);

    for(int i=1;i<=n;i++)cout<<ans[i]<<endl;

}

G题 Isosceles Trapezium

题目大意：

给出平面内 $n$ 个带有权值的点，输出构成等腰梯形的点的最大权值和

思路解析：

我们首先考虑等腰梯形的性质，我们可以发现他的平行边的垂直平分线是相同的，并且两线的中点不为同一个点，所以我们用O(n^2)求出每条边的垂直平分线，并且记录两个端点的价值，这样我们就可以枚举垂直平分线想相同的点来求得答案。

AC代码：

//假装这里有代码

推广一波小飞龙博客：戳这里@不会飞的小飞龙