2.3 数据校验的基本原理

（1）数据校验的必要性：

受元器件质量、电路故障或其他干扰等影响，数据在处理、传输、存储的过程中可能会出现错误。如果设计硬件层面的错误检测机制，可以减少基于软件检错的代价。

（2）校验的基本原理：

增加冗余码（校验位）：

发送方对被发送的信息基于校验位做某种运算，得到一个编码；
发送方将编码连同信息一并发送给接受方；
接收方会根据信息和校验位，再去执行与发送方相关的运算，然后评测收到的数据是否出现了错误；

（3）码距：

同一个编码中，任意两个合法编码之间的不同二进制数位数的最小值；

如： 0011与0001的码距是1；（一位错误无法识别）
0000、0011、0101、0110、1001、1010、1100、1111等编码的码距为2；
（码距是任意两个编码的不同二进制位的最小值，因此即使0000和1111的码距是4，但最小值仍然为2）

校验码中增加冗余项的目的就是为了增大码距，使得错误发生以后，接收方至少能够检测出错误；

（4）码距与检错或纠错能力之间的关系

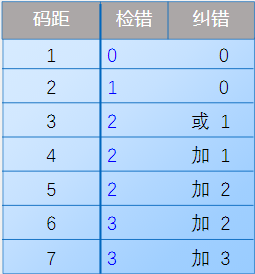
1、码距 >= e + 1: 可以检测e个错误
2、码距 >= 2 * t + 1: 可以纠正t个错误
3、码距 >= e + t + 1: 可以纠正t个错误，同时检测e个错误 （e >= t）

（5）码距选择的因素：

看来似乎码距越大，纠错和检测的能力越强；
但是，校验位增加了，会使得编码的效率降低，编码电路也会复杂；

因此选择码距必须考虑信息发生差错的概率和系统能容许的最小差错率；

2.4 奇偶校验（对校验原理的实例化）

（1）奇偶校验

奇偶校验的校验位只有一位：

编码： 根据有效信息计算校验信息位，使得校验码中1的个数满足奇/偶校验的要求；

如：
1、0001 -> 00011 （偶校验，校验码中1的个数为偶数）
校验位$ P = D_1 \bigoplus D_2 \bigoplus … \bigoplus D_n$

2、0001 -> 00010 （奇校验，校验码中1的个数为奇数）
校验位$ P = \overline{D_1 \bigoplus D_2 \bigoplus … \bigoplus D_n}$

（2）检错方法与电路：

例如，对于奇校验码来说信息传输发生图示错误：

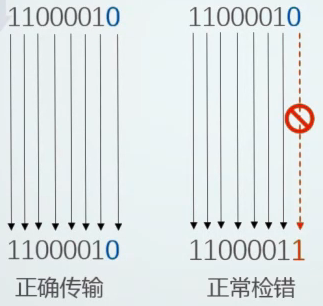
则$ G = \overline{C \bigoplus D_1 \bigoplus D_2 \bigoplus … \bigoplus D_7}，(C为校验位)$

$G = 0$表示数据正常，否则表示出错;

检测的硬件电路如图示：

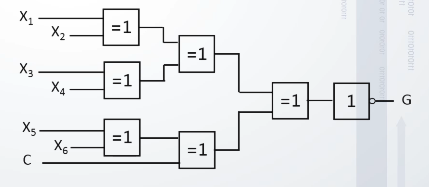
再如，对于偶校验码来说信息传输发生图示错误：

则$ G = C \bigoplus D_1 \bigoplus D_2 \bigoplus … \bigoplus D_7$

$G = 0$表示数据正常，否则表示出错;

检测的硬件电路如图示：

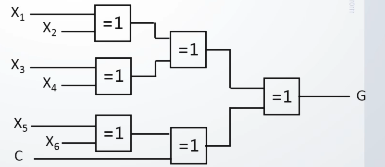
（3）奇偶校验的特点：

• 编码与检错简单
• 编码效率高
• 不能检测偶数位错误，无错结论不可靠，是一种错误检测码
• 不能定位错误，故不具备纠错能力

（4）奇偶校验的码距：

由上一节码距和检错的能力关系可知：

奇偶校验码只能检查一位的错误，因此奇偶校验的码距为2；

什么意思呢？

例如有一串原码：000、001、010、011、100、101、110、111
则这串原码对应的奇校验码为（以奇校验为例）：
0001、0010、0100、0111、1000、1011、1101、1110

加上校验位后，该编码系统的最小码距为2；

奇偶校验码的码距为2，这句话的全称应该是：利用奇偶校验码来查错的编码系统的合法编码之间的最小码距为2。

（5）改进的奇/偶校验：（双向奇偶校验、方块校验、垂直水平校验）

在传统奇偶校验的基础之上，加上纵向校验；

以偶检验为例，图示最后一行就是对当前列做偶检验；

改进后，可以对通过行列定位对一位错误做修改，如：

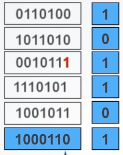
对于一部分偶数位错误可以进行检错，如：

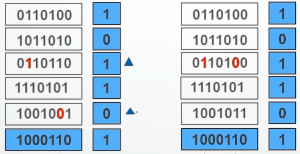
但是也有不能检错的情况，如：

（6）奇偶校验的应用：

因为奇偶校验对无错的结果不可靠，所以通常用于近距离，可靠性高的场合；

如：部分主机内存中使用的是奇偶校验