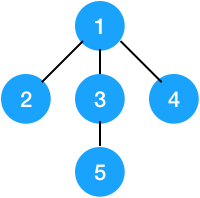
并查集 是一种树型的数据结构，用于处理一些不相交集合的合并和查询问题。在使用中常常以森林来表示。

上图中记录父情节点的 fa 数组为：

fa[1] = 1; fa[2] = 1; fa[3] = 1; fa[4] = 1; fa[5] = 3;

初始化

初始化的时候将自己的父亲设置为自己，使自己成为一个单独的集合。

for (int i = 0;i < maxn;i++) {
    fa[i] = i;
}

寻找根结点

使用递归实现，如果 fa[i] != i，那么代表这个结点并不是根结点，继续 get(fa[i])。

int get(int x) {
    if (fa[x] == x) {
        return fa[x];
    } else {
        return get(fa[x]);
    }
}

合并

将两个元素放到一个集合当中。注意，合并的必须是根结点

void merge(int x, int y) {
    x = get(x), y = get(y);
    if (x != y) {
        fa[x] = y;
    }
}

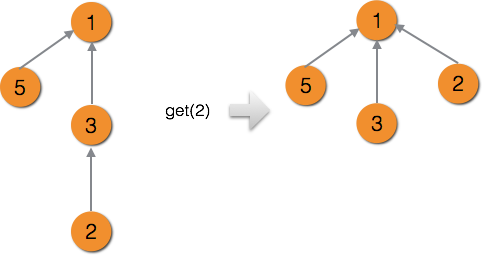
对查找根结点的优化——路径压缩

如果并查集的结构刚好是个链，那么查找最末端结点的根结点时间复杂度将会很高。

我们并不在乎结构到底是怎么样的，只关心他的根结点是谁。可以直接把查询路径上的所有结点的 fa[i] 都赋值成为根结点。实现这一步只需要在我们之前的查询函数上面进行很小的改动。

int get(int x) {
    if (fa[x] == x) {
        return fa[x];
    } else {
        return fa[x] = get(fa[x]);
    }
}

下面图片是路径压缩前后的对比。

试一试

Kruskal 最小生成树算法