递归

递归的定义与实现

前提条件

当 原问题 与 问题边界 之间的 每个变换步骤具有相似性时 就可以考虑用 递归 或 递推 来求解

变换步骤（递归）

对于递归算法，可以通过以下三个操作来求解

1. 自身调用自身

缩小问题规模空间 ，

这意味着程序尝试寻找在 原问题 与 问题边界 之间的 变化路线，并向 正在探索 的路线上迈出一步

2. 回溯时还原现场（搜索失败）

尝试求解 规模缩小以后的问题，

如果失败，程序需要 重新回到当前问题 去寻找 其它的变换路线，

因此把 当前问题 缩小为 子问题 时所做的 对当前问题状态产生影响的事情 应 全部失效

3. 扩展（搜索成功）

找到了 规模缩小以后的问题 的答案， 那么将答案 扩展到当前问题。

如果失败，就 重新返回 当前问题，继续寻找 当前答案 的 其它变换路线，直至 确定当前问题无法求解

总结

简洁的说，就是 缩小，求解，扩展

简单枚举形式

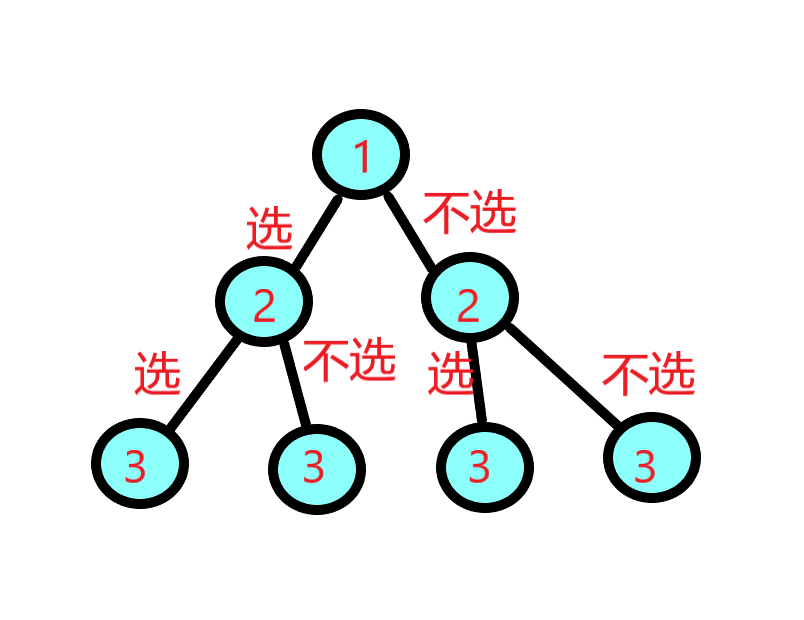
指数型枚举

等价于每个整数都有两种可能，选 或者 不选

也就是说，这颗搜索树上的每一个节点都有两个分支，

每次将尚未确定的整数减少 1，从而转换成一个更小的同类问题

void dfs(int u){
    if (u == n)
    {
        for (int i = 0; i < n; i ++ )
            if (a[i] == true)
                printf("%d ",i + 1);
        puts("");
        return;
    }

    dfs(u + 1);
    a[u] = true;
    dfs(u + 1);
    a[u] = false;
}

组合型枚举

及时确定无解，就不需要到达问题边界才返回结果了

void dfs(int u){
    if (ch.size() > m || ch.size() + (n - u + 1) < m) return;
    if (u == n + 1)
    {
        for (int i = 0; i < ch.size(); i ++ )
            printf("%d ", ch[i]);
        puts("");
        return;
    }

    dfs(u + 1);
    ch.push_back(u);

    dfs(u + 1);
    ch.pop_back();
}

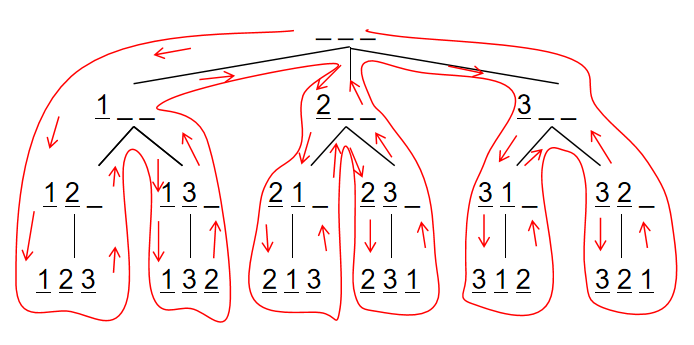
排列型枚举

在每次递归中，我们尝试把每个可用的数作为数列中的下一个数，

求解把剩余 n - 1 个整数按任意次序排列，这个更小的子问题

int st[N];//存储方案
bool used[N];//标记数字是否被用过，true表示被用过，false表示没被用过
int n;

void dfs(int u) {   //当前枚举第u位
    if (u > n) {
        for (int i = 1; i <= n; i ++ ) 
            printf("%d ", st[i]);   //打印方案
        puts("");
        return ;
    }

    for (int i = 1; i <= n; i ++ ) {    //依次枚举每个数
        if (!used[i]) {                 //当前数可用
            st[u] = i;
            used[i] = true;
            dfs(u + 1);

                            //恢复现场
            st[u] = 0;      //可省略
            used[i] = false;//不可省
        }
    }
}

int main() {
    scanf("%d", &n);

    dfs(1);

    return 0;
}