一、并查集

问题
有 $n$ 个集合,每个集合有且仅有一个元素,且所有元素均不相同。
现在你需要处理集合的合并,并且回答某两个元素是否属于同一个集合。
分析:
暴力点:直接数组维护。
聪明一点?
设 par[u] 表示元素 $u$ 指向的元素
两个优化:
- 路径压缩
- 按秩合并
均摊的单次时间复杂度 $O(\alpha(n))$
总时间复杂度 $O(n\alpha(n))$
Code:
int par[MX];
void init(int n) {
for (int i = 1; i <= n; ++i) {
par[i] = i;
sz[i] = 1;
}
}
int find(int u) { // 路径压缩
if (par[u] == u) return u;
return par[u] = find(par[u]);
}
bool same(int u, int v) {
return find(u) == find(v);
}
void merge(int u, int v) { // 按秩合并/启发式合并
u = find(u); v = find(v);
par[v] = u;
if (sz[u] < sz[v]) swap(u, v);
par[v] = u;
sz[u] += sz[v];
}
例题:搭配购买
一个商店里卖 $n$ 种商品,商品已经被老板编号为 $1, 2, \cdots, n$,并且每个商品都有一个价值,但是商店的老板是个很奇怪的人,他会告诉你一些商品要搭配起来买才卖,也就是说买一个商品则与其有搭配的商品都要买,你希望用现有的钱买到尽可能多价值的商品。
$n \leqslant 10000$,搭配数 $m \leqslant 5000$,你拥有的钱 $w \leqslant 10000$
分析:
构造并查集后跑01背包即可
C++ 代码
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)
using std::cin;
using std::cout;
using std::swap;
using std::vector;
struct UnionFind {
vector<int> d, co, w;
UnionFind(int n): d(n, -1), co(n), w(n) {}
int find(int x) {
if (d[x] < 0) return x;
return d[x] = find(d[x]);
}
bool unite(int x, int y) {
x = find(x); y = find(y);
if (x == y) return false;
if (d[x] > d[y]) swap(x, y);
d[x] += d[y];
d[y] = x;
co[x] += co[y];
w[x] += w[y];
return true;
}
bool same(int x, int y) { return find(x) == find(y); }
int size(int x) { return -d[find(x)]; }
};
inline void chmax(int &a, int b) { if (a < b) a = b; }
const int MX = 10005;
int dp[MX];
int main() {
int n, m, w;
cin >> n >> m >> w;
UnionFind uf(n);
rep(i, n) cin >> uf.co[i] >> uf.w[i];
rep(i, m) {
int u, v;
cin >> u >> v;
--u; --v;
uf.unite(u, v);
}
rep(i, n) if (uf.find(i) == i) {
int a = uf.co[i];
int b = uf.w[i];
for (int j = w; j >= a; --j) {
chmax(dp[j], dp[j - a] + b);
}
}
cout << dp[w] << '\n';
return 0;
}
例题2: [BOI2003]团伙
给定 $n$ 个人,他们之间有两个种关系,朋友与敌对。可以肯定的是:
- 与我的朋友是朋友的人是我的朋友
- 与我敌对的人有敌对关系的人是我的朋友
现在这 $n$ 个人进行组团,两个人在一个团队内当且仅当他们是朋友。
求最多的团体数。
分析:
对于每对关系:
如果是朋友,那么直接合并
如果是敌人,那么标记为敌对关系, 然后枚举第三者判断是否是敌人的敌人
并查集统计即可
C++ 代码
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)
using std::cin;
using std::cout;
using std::swap;
using std::vector;
struct UnionFind {
vector<int> d;
UnionFind(int n): d(n, -1) {}
int find(int x) {
if (d[x] < 0) return x;
return d[x] = find(d[x]);
}
bool unite(int x, int y) {
x = find(x); y = find(y);
if (x == y) return false;
if (d[x] > d[y]) swap(x, y);
d[x] += d[y];
d[y] = x;
return true;
}
bool same(int x, int y) { return find(x) == find(y); }
int size(int x) { return -d[find(x)]; }
};
int main() {
int n, m;
cin >> n >> m;
UnionFind uf(n);
vector e(n, vector<bool>(n));
rep(i, m) {
char opt;
int p, q;
cin >> opt >> p >> q;
--p; --q;
if (opt == 'F') uf.unite(p, q);
else {
e[p][q] = e[q][p] = true;
rep(i, n) {
if (e[p][i]) uf.unite(q, i); // p和i是敌人,p和q是敌人,所以q和i是朋友
if (e[q][i]) uf.unite(p, i);
}
}
}
int ans = 0;
rep(i, n) ans += uf.find(i) == i;
cout << ans << '\n';
return 0;
}
二、树状数组
.jpg)
引入
树状数组处理的问题一般有如下形式:
给定一个数组 $a[1 \cdots n]$,支持以下两种操作:
- 修改:给 $a[i]$ 加上 $v$
- 查询:询问 $a[1] + a[2] + \cdots + a[i]$
思想
每个正整数都可以表示为若干个 $2$ 的幂次之和。
类似的,每次求前缀和,我们也希望将区间 $[1, i]$ 分解成 $\log_2 i$ 个子集的和。
也就是如果 $i$ 的二进制表示中如果有 $k$ 个 $1$,我们就希望将其分解为 $k$ 个子集之和
基于这种思想,我们可以制作一张表格:
内容代表该”子集”所包含的 $a$ 数组的元素
例如,下标为 $8$ 的子集包含了 $a[1 \cdots 8]$,而下标为 $5$ 的子集只包含 $a[5]$。

下表就是一个实际的例子:
用 sum 表示子集和
比如求 $7(111)$ 的前缀和,只需计算 $sum[7] + sum[6] + sum[4]$
求 $10(1010)$ 的前缀和,只需要计算 $sum[10] + sum[8]$

我们可以用下图更直观的理解:
深色方块代表下标对应的值 $a[i]$,浅色方块代表还要维护的别的下标对应的值 $a[k \cdots i - 1]$
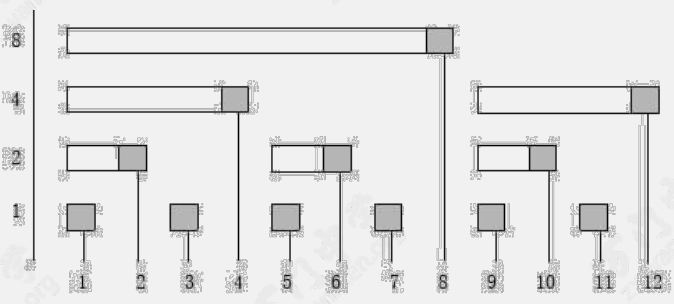
实现
现在留下的问题就是,子集要如何划分。
观察下表
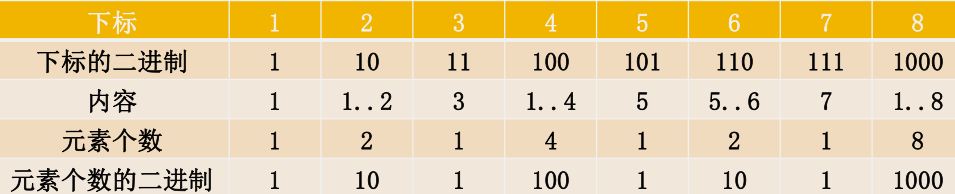
可以发现,元素个数的二进制就是下标的二进制表示最低位 1 所在的位置的数。
如何求一个数 $x$ 的二进制最低非 $0$ 位对应的数?
朴素方法:$O(\log_2 x)$ 枚举
Lowbit(x) 函数!
$C(x) = x - (x \ and \ (x - 1))$
x and (x - 1) 将 $x$ 最低位的 $1$ 以及后面所有的 $0$ 都变成了 $0$,然后再被 $x$ 减去,这就是我们要的数。
$C(x) = x \ and \ -x$
计算机里存储整数用的是数字的补码。
正数的补码就是本身的二进制码。
相反数的补码等于其反码加一。
假设 $x$ 的二进制为 $a1b$ ($a$ 为 $01$ 串,$b$ 全是 $0$)
$-x$ 就是 $(\sim a)1b$,两者 and 就得到了 $1b$,就是我们想要的数。
查询
根据下图可以得到查询 $a[1 \cdots i]$ 前缀和的方法
ans = 0
while (i > 0) ans += sum[i], i -= C(i);
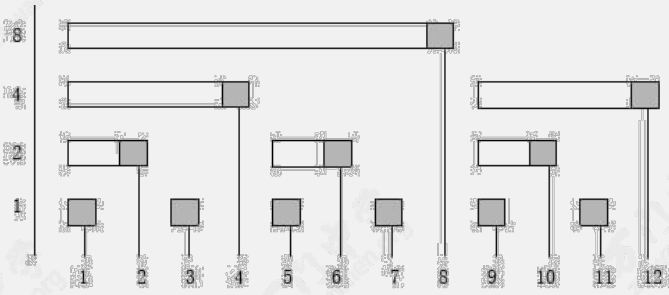
下图为 查询树
需要相加的项的个数为 $i$ 的二进制表示中包含的 $1$ 的个数。
时间复杂度为 $O(\log_2 i)$
修改
当 $a[i]$ 要加上 $v$ 时,我们需要关心有哪些子集和包含了这个需要被修改的元素 $a[i]$。
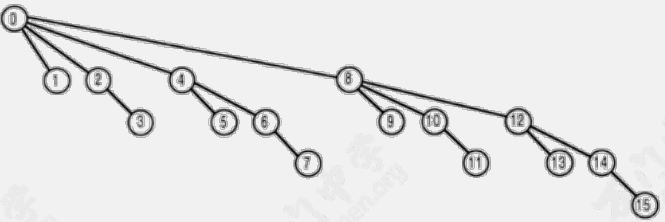
可以发现,每个深色方块上面的那些长方形都代表了包含该元素的子集。

与查询不同的是,这里是每一步循环给下标加上 $C(i)$
change(i, v):
while (i <= n) sum[i] += v, i += C(i)
下图是 更新树
由于树的深度至多是 $\log_2 n$,所以修改操作的时间复杂度也是 $O(\log_2 n)$。
常用技巧
查询区间和:$a[x \cdots y]$
只需要查询 $Query(y) - Query(x - 1)$
单点查询:$a[x]$
最简单的方法:$Query(x) - Query(x - 1)$
但是要执行两次查询。
观查询察树,$a[x] = sum[x] - (Query(x - 1) - Query(LCA(x, x - 1)))$
get_value(i):
ans = sum[i]
lca = i - C(i)
i--
while i != lca:
ans -= sum[i]
i -= C(x)
return ans
假设元素非负,查询某个前缀和对应的前缀下标 $i$
因为下标为 $2$ 的幂次的子集包含了从开始的元素到自己的所有元素。
所以我们可以根据更新树进行二分,初始步长为 $n$,之后每次减半。

get_index(v):
i = 0
len = n
while len != 0:
test_id = i + len
if (v >= sum[test_id]):
i = test_id
v -= sum[test_id]
len /= 2
return i
初始化树状数组:
朴素做法,一个一个插入:$O(n\log n)$
维护一个前缀和数组 $pre[x] = sum(a[1 \cdots x])$
$sum[x] = pre[x] - pre[x - C(x)]$
模板题1: Range Sum Query (RSQ)
Code:
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)
using std::cin;
using std::cout;
using std::vector;
template<typename T>
struct BIT {
int n;
vector<T> d;
BIT(int n=0):n(n),d(n+1) {}
void add(int i, T x=1) {
for (i++; i <= n; i += i&-i) {
d[i] += x;
}
}
T sum(int i) {
T x = 0;
for (i++; i; i -= i&-i) {
x += d[i];
}
return x;
}
T sum(int l, int r) {
return sum(r-1) - sum(l-1);
}
};
int main() {
int n, m;
cin >> n >> m;
BIT<int> t(n);
rep(_, m) {
int type, x, y;
cin >> type >> x >> y;
--x;
if (type == 0) t.add(x, y);
else {
int ans = t.sum(x, y);
cout << ans << '\n';
}
}
return 0;
}
模板题2: 树状数组 1 :单点修改,区间查询
Code:
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)
using std::cin;
using std::cout;
using std::vector;
template<typename T>
struct BIT {
int n;
vector<T> d;
BIT(int n=0):n(n),d(n+1) {}
void add(int i, T x=1) {
for (i++; i <= n; i += i&-i) {
d[i] += x;
}
}
T sum(int i) {
T x = 0;
for (i++; i; i -= i&-i) {
x += d[i];
}
return x;
}
T sum(int l, int r) {
return sum(r-1) - sum(l-1);
}
};
int main() {
int n, m;
cin >> n >> m;
BIT<int> t(n);
rep(_, m) {
int type, x, y;
cin >> type >> x >> y;
--x;
if (type == 0) t.add(x, y);
else {
int ans = t.sum(x, y);
cout << ans << '\n';
}
}
return 0;
}
模板题3: Range Add Query (RAQ)
Code:
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)
using std::cin;
using std::cout;
using std::vector;
template<typename T>
struct BIT {
int n;
vector<T> d;
BIT(int n=0):n(n),d(n+1) {}
void add(int i, T x=1) {
for (i++; i <= n; i += i&-i) {
d[i] += x;
}
}
T sum(int i) {
T x = 0;
for (i++; i; i -= i&-i) {
x += d[i];
}
return x;
}
T sum(int l, int r) {
return sum(r-1) - sum(l-1);
}
void imos(int l, int r, int x) {
add(l, x);
add(r, -x);
}
};
int main() {
int n, m;
cin >> n >> m;
BIT<int> t(n);
rep(_, m) {
int type, x;
cin >> type >> x;
--x;
if (type == 0) {
int y, k;
cin >> y >> k;
t.imos(x, y, k);
}
else {
int ans = t.sum(x);
cout << ans << '\n';
}
}
return 0;
}
模板题4: 树状数组 2 :区间修改,单点查询
Code:
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)
using std::cin;
using std::cout;
using std::vector;
using ll = long long;
template<typename T>
struct BIT {
int n;
vector<T> d;
BIT(int n=0):n(n),d(n+1) {}
void add(int i, T x=1) {
for (i++; i <= n; i += i&-i) {
d[i] += x;
}
}
T sum(int i) {
T x = 0;
for (i++; i; i -= i&-i) {
x += d[i];
}
return x;
}
T sum(int l, int r) {
return sum(r-1) - sum(l-1);
}
void imos(int l, int r, int x) {
add(l, x);
add(r, -x);
}
};
int main() {
int n, m;
cin >> n >> m;
BIT<ll> t(n);
ll pre = 0;
rep(i, n) {
int a; cin >> a;
t.add(i, a - pre);
pre = a;
}
rep(_, m) {
int type, x;
cin >> type >> x;
--x;
if (type == 1) {
int y, k;
cin >> y >> k;
t.imos(x, y, k);
}
else {
ll ans = t.sum(x);
cout << ans << '\n';
}
}
return 0;
}
例题: 数星星
二维平面上有 $n$ 个点 $(x[i], y[i])$
现在请你求出每个点左下角的点的个数。
$n \leqslant 15000$,$0 \leqslant x, y \leqslant 32000$
分析:
直接对每个点 $(x_i, y_i)$,查询矩形 $(0, 0) – (x_i, y_i)$ 里有几个点
过于暴力,而且二维树状数组空间也存不下。
注意到在 $i$ 左下角的点也就是满足 $x \leqslant x_i, y \leqslant y_i$ 的点
可以运用扫描线的思想,把一维限制直接去掉。
从小到大枚举 $y_i$,每次把 $y \leqslant y_i$ 的点插入一个集合 $S$
然后在 $S$ 里查询 $x \leqslant x_i$ 的个数即可
只需用树状数组来维护 $S$ 集合中的数
时间复杂度:$O(n\log n)$
C++ 代码
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)
using std::cin;
using std::cout;
using std::vector;
using P = std::pair<int, int>;
template<typename T>
struct BIT {
int n;
vector<T> d;
BIT(int n=0):n(n),d(n+1) {}
void add(int i, T x=1) {
for (i++; i <= n; i += i&-i) {
d[i] += x;
}
}
T sum(int i) {
T x = 0;
for (i++; i; i -= i&-i) {
x += d[i];
}
return x;
}
T sum(int l, int r) {
return sum(r-1) - sum(l-1);
}
};
int main() {
int n;
cin >> n;
vector<P> p(n);
rep(i, n) cin >> p[i].first >> p[i].second;
// 因为输入就是按 y 坐标升序给出,y 坐标相同的按 x 坐标增序给出
// 所以我们不需要排序,直接计算即可
BIT<int> t(32001);
vector<int> ans(n);
for (auto& [x, y] : p) {
int v = t.sum(x);
t.add(x);
ans[v]++;
}
rep(i, n) cout << ans[i] << '\n';
return 0;
}
三、线段树
区间合并线段树
例题: P2894 [USACO08FEB]Hotel G
为了整洁,我们用结构体来装线段树。父节点的最大连续空房的个数 $num$,无法由子节点直接得到,因为有可能两个子节点左右相接得到更大的 $num$,所以我们还需要维护左右子节点接近边界的最大连续空房的个数。
C++ 代码
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)
using std::cin;
using std::cout;
const int MX = 50005;
struct Node {
int len; // 区间长度
int num; // 区间最大连续 0 的个数
int lNum; // 从左侧开始的最大长度 贴着最左边连续空房
int rNum; // 从右侧开始的最大长度 贴着最右边连续空房
int tag; // 0 表示无,1 表示住满了,2 表示全退了
} tree[MX*4];
inline int lc(int p) { return p<<1; }
inline int rc(int p) { return p<<1|1; }
inline void chmax(int& x, int y) { if (x < y) x = y; }
void pushUp(int p) {
if (tree[lc(p)].num == tree[lc(p)].len) { // 左边全是空房
tree[p].lNum = tree[lc(p)].num + tree[rc(p)].lNum;
}
else {
tree[p].lNum = tree[lc(p)].lNum;
}
if (tree[rc(p)].num == tree[rc(p)].len) { // 右边全是空房
tree[p].rNum = tree[rc(p)].num + tree[lc(p)].rNum;
}
else {
tree[p].rNum = tree[rc(p)].rNum;
}
tree[p].num = tree[lc(p)].rNum + tree[rc(p)].lNum; // 中间空房拼起来
chmax(tree[p].num, tree[lc(p)].num);
chmax(tree[p].num, tree[rc(p)].num);
}
void buildTree(int p, int l, int r) {
tree[p].len = r-l+1;
if (l == r) { // 叶节点
tree[p].num = tree[p].lNum = tree[p].rNum = 1;
return;
}
int mid = (l+r)/2;
buildTree(lc(p), l, mid);
buildTree(rc(p), mid+1, r);
pushUp(p);
}
void moveTag(int p, int l, int r, int tag) {
if (tag == 1) { // 全入住
tree[p].num = tree[p].lNum = tree[p].rNum = 0;
tree[p].tag = 1;
}
else { // 全退房
tree[p].num = tree[p].lNum = tree[p].rNum = r-l+1;
tree[p].tag = 2;
}
}
void pushDown(int p, int l, int r) {
if (!tree[p].tag) return;
int mid = (l+r)/2;
moveTag(lc(p), l, mid, tree[p].tag);
moveTag(rc(p), mid+1, r, tree[p].tag);
tree[p].tag = 0;
}
int query(int p, int l, int r, int k) {
if (l == r) return l;
pushDown(p, l, r);
int mid = (l+r)/2;
if (tree[lc(p)].num >= k) return query(lc(p), l, mid, k);
if (tree[lc(p)].rNum + tree[rc(p)].lNum >= k) return mid + 1 - tree[lc(p)].rNum;
if (tree[rc(p)].num >= k) return query(rc(p), mid+1, r, k);
return 0;
}
void checkIn(int p, int l, int r, int ql, int qr) { // 入住
if (ql <= l and r <= qr) {
tree[p].num = tree[p].lNum = tree[p].rNum = 0;
tree[p].tag = 1;
return;
}
pushDown(p, l, r);
int mid = (l+r)/2;
if (ql <= mid) checkIn(lc(p), l, mid, ql, qr);
if (mid < qr) checkIn(rc(p), mid+1, r, ql, qr);
pushUp(p);
}
void checkOut(int p, int l, int r, int ql, int qr) { // 退房
if (ql <= l and r <= qr) {
tree[p].num = tree[p].lNum = tree[p].rNum = r-l+1;
tree[p].tag = 2;
return;
}
pushDown(p, l, r);
int mid = (l+r)/2;
if (ql <= mid) checkOut(lc(p), l, mid, ql, qr);
if (mid < qr) checkOut(rc(p), mid+1, r, ql, qr);
pushUp(p);
}
int main() {
int n, m;
cin >> n >> m;
buildTree(1, 1, n);
rep(i, m) {
int type;
cin >> type;
if (type == 1) {
int d;
cin >> d;
int p = query(1, 1, n, d);
cout << p << '\n';
if (p) checkIn(1, 1, n, p, p+d-1);
}
else {
int x, d;
cin >> x >> d;
checkOut(1, 1, n, x, x+d-1);
}
}
return 0;
}
KD 树
K-Dimension tree,简称 KD树,顾名思义,是能够存储 $K$ 维数据的一颗树。$\rm{KD}$ 树是二叉搜索树的拓展,主要用于多维空间关键数据的搜索,例如范围搜索和最近邻搜索。
$\rm{BST}$、$\rm{AVL}$、$\rm{Treap}$ 和 $\rm{Splay}$ 等二叉搜索树,其节点存储的都是一维信息,一维的信息很容易处理,直接按照数据大小比较,左子树小于根,右子树大于根即可,多维数据需要选择一个维度 $D_i$,然后在维度 $D_i$ 上进行大小比较。例如,二维平面上的两个点 $A(2, 4)$,$B(5, 3)$,如果按照第一维比较,$A < B$;如果按照第二维比较,$A > B$。
1. 创建 KD 树
$\rm{KD}$ 树是二叉树,表示对 $K$ 维数据的划分,每个节点对应 $K$ 维空间中的超矩形区域,$\rm{KD}$ 树可以省去大部分数据点的搜索,提高效率。
$K$ 维数据在划分子树时,需要考虑两个问题:
- 选择哪个维度划分?
- 选择哪个划分点,可以使左右子树大小大致相等?
第一个问题是如何比较,第二个问题是尽量平衡。众所周知,二叉搜索树在极不平衡的情况下,退化为线性,效率最差;在平衡的情况下,时间复杂度为 $O(\log n)$。
1) 维度划分
选择哪一维进行划分,即选择哪一维作为分辨器。$\rm{KD}$ 树可以根据不同的用途选择不同的分辨器。最常见的是轮转法和最大方差法。
轮转法:按照维度轮流作为分辨器
一些练习题
并查集:

