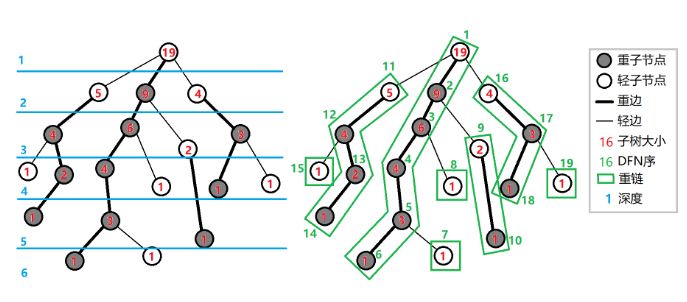
一、最近公共祖先 LCA

树上信息的处理

我们拿到树的问题的时候，它们的画风通常都是这个样子的：

• 给定一颗 $n$ 个点的边带权无根树，给出 $m$ 个询问，对于第 $i$ 个询问，你需要求从 $s_i$ 出发到 $t_i$ 终止的最短路径上面的一些信息。

更特殊地，比如下面这个问题：

• 给定一颗 $n$ 个点的边带权无根树，给出 $m$ 个询问，对于第 $i$ 个询问，你需要求 $s_i$ 到 $t_i$ 的最短路径的长度。

要求越快越好。

首先显然直接路径只有一条。
因为没有根，我们定 $1$ 作为根会方便一些。
有了根之后，我们就有了每个点到根的距离 dist[u]。
我们看一下 $(u, v)$ 两点之间的路径是怎么样的：

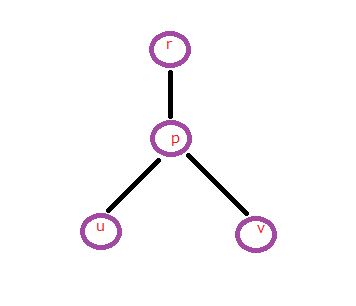
容易发现，$u$ 到 $v$ 的距离就是 dist[u] + dist[v] - 2 * dist[p]，其中 $p$ 是 $u$ 和 $v$ 的最近公共祖先。
那么我们只需要求出 LCA(u, v) 就几乎解决完问题了。

最近公共祖先

关于 LCA，有几种常用的算法：

• 倍增
• Tarjan
• 轻重链剖分

LCA：倍增法

我们记一个点的 $k$ 级祖先是它往根节点方向走 $k$ 步得到的节点。
记 fa[u][i] 表示点 $u$ 的第 $2^i$ 级祖先。
容易用边 dfs 边递推的方式计算得到

$$fa[u][i] = fa[fa[u][i - 1]][i - 1]$$

模板题： 最近公共祖先（LCA）

Code:

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using std::cin;
using std::cout;
using std::swap;
using std::vector;

struct LCA {
    int n, bi;
    vector<int> dep;
    vector<vector<int>> to, anc;
    LCA(int n): n(n), dep(n), to(n) {}

    void addEdge(int a, int b) {
        to[a].push_back(b);
        to[b].push_back(a);
    }

    void init(int root = 0) {
        bi = 0;
        while (1<<bi <= n) ++bi;
        anc = vector(n, vector<int>(bi, -1));
        dfs(root);
        rep(i, bi - 1)rep(j, n) anc[j][i + 1] = (anc[j][i] == -1 ? -1 : anc[anc[j][i]][i]);
    }

    void dfs(int v, int p = -1) { 
        dep[v] = dep[p] + 1;
        anc[v][0] = p;
        for (int u : to[v]) {
            if (u == p) continue;
            dfs(u, v);
        }
    }

    int lca(int x, int y) {
        if (dep[x] < dep[y]) swap(x, y);
        int d = dep[x] - dep[y];
        for (int i = bi - 1; i >= 0; --i) {
            if (1<<i <= d) x = anc[x][i], d -= 1<<i; 
        }
        if (x == y) return x;
        for (int i = bi - 1; i >= 0; --i) {
            if (anc[x][i] != anc[y][i]) x = anc[x][i], y = anc[y][i];
        }
        return anc[x][0];
    }

    int dist(int x, int y) {
        return dep[x] + dep[y] - 2 * dep[lca(x, y)];
    }
};

int main() {
    std::ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int n, m, s;
    cin >> n >> m >> s;

    LCA g(n);
    rep(i, n - 1) {
        int x, y;
        cin >> x >> y;
        --x; --y;
        g.addEdge(x, y);
    }

    g.init(s - 1);

    rep(mi, m) {
        int a, b;
        cin >> a >> b;
        --a; --b;
        int ans = g.lca(a, b) + 1;
        cout << ans << '\n';
    }

    return 0;
}

例题： 閉路

题意：查询树上两点之间的距离

分析：

$dist(x, y) = dep(x) + dep(y) - 2 \times dep(lca(x, y))$

Code:

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using std::cin;
using std::cout;
using std::swap;
using std::vector;

struct LCA {
    int n, bi;
    vector<int> dep;
    vector<vector<int>> to, anc;
    LCA(int n): n(n), dep(n), to(n) {}

    void addEdge(int a, int b) {
        to[a].push_back(b);
        to[b].push_back(a);
    }

    void init(int root = 0) {
        bi = 0;
        while (1<<bi <= n) ++bi;
        anc = vector(n, vector<int>(bi, -1));
        dfs(root);
        rep(i, bi - 1)rep(j, n) anc[j][i + 1] = (anc[j][i] == -1 ? -1 : anc[anc[j][i]][i]);
    }

    void dfs(int v, int p = -1) { 
        dep[v] = dep[p] + 1;
        anc[v][0] = p;
        for (int u : to[v]) {
            if (u == p) continue;
            dfs(u, v);
        }
    }

    int lca(int x, int y) {
        if (dep[x] < dep[y]) swap(x, y);
        int d = dep[x] - dep[y];
        for (int i = bi - 1; i >= 0; --i) {
            if (1<<i <= d) x = anc[x][i], d -= 1<<i; 
        }
        if (x == y) return x;
        for (int i = bi - 1; i >= 0; --i) {
            if (anc[x][i] != anc[y][i]) x = anc[x][i], y = anc[y][i];
        }
        return anc[x][0];
    }

    int dist(int x, int y) {
        return dep[x] + dep[y] - 2 * dep[lca(x, y)];
    }
};

int main() {
    int n;
    cin >> n;

    LCA g(n);
    rep(i, n - 1) {
        int x, y;
        cin >> x >> y;
        --x; --y;
        g.addEdge(x, y);
    }

    g.init();

    int q;
    cin >> q;
    rep(qi, q) {
        int a, b;
        cin >> a >> b;
        --a; --b;
        int ans = g.dist(a, b) + 1;
        cout << ans << '\n';
    }

    return 0;
}

二、树链剖分（轻重链剖分）

树链剖分的思想是通过 轻重边剖分 将树分为多条链，保证每个点属于且仅属于一条链，然后再通过数据结构（如树状数组、$\rm SBT$、$\rm splay$、线段树等）来维护每一条链。
树链剖分可以维护树上路径信息，每条重链就相当于一段区间，用数据结构去维护。把所有的重链首尾相接，放到一个数据结构上，然后维护这一个整体即可。
树链剖分的用处比倍增多，倍增能做的题 树剖一定能做，反过来则否。树链剖分的代码复杂度不算特别高，调试也不难，在高级的比赛里，树链剖分是必备知识。

思维：转化、预处理

将（有根树）分割成若干条不相交链 $l$

• $l = [u_1, u_2, \cdots, u_p], 1 \leqslant p \leqslant n$
• $fa[u_i] = u_{i-1}, \forall 2 \leqslant i \leqslant p$
• 树上每个顶点恰好在一条链上，这些链可用于维护树上路径相关的信息

每条链为线性结构，可使用其他数据结构维护它
树链剖分一般指重链剖分
树上任意一条路径可以由 $O(\log n)$ 条链（或链的一部分）相接而成
对每条链 $[u_1, u_2, \cdots, u_p]$，其每个节点有连续且唯一的编号，且恰为节点的 dfs序，即 ${\rm dfn}[u_i] = {\rm dfn}[u_{i-1}] + 1$
因此，可将树上路径问题转化为 $\log n$ 个区间问题，如可使用线段树等维护
树剖也可求 $\rm LCA$，或在 $\rm LCA$ 的基础上处理路径问题

我们引入“重边”（读音 $\rm zhong$）与“轻边”的概念。
对每个非叶节点，我们找到 包含最多节点 的孩子（如有多个选任意一个），也可以理解为这个孩子节点的子树最大。
连接它与这个孩子的边被称为重边，连接它与其他孩子的边都是轻边。
与重边对应的节点是 重儿子，与轻边对应的节点是 轻儿子。
完成这个步骤后，树的每条边要么是重边，要么是轻边；而且每个非叶节点 必定有且仅有一条重边连向它的某个孩子
我们把 重边连接而成的链，称为重链。
可以证明，树上任意一条简单路径必定只经过了不超过 $O(\log n)$ 条重链（或重链的一部分）和不超过 $O(\log n)$ 条轻边。

一些规定：

fa[v]：节点 $v$ 在树上的父亲
dep[v]： 节点 $v$ 在树上的深度
siz[v]： 节点 $v$ 的子树大小
hson[v]：节点 $v$ 的重儿子
top[v]：节点 $v$ 所在的重链顶部编号（深度最小）
dfn[v]：节点 $v$ 的 dfs序
rnk[v]：$\rm dfs$ 序对应的节点编号，rnk[dfn[v]] = v

第一次 $\rm dfs$：常规树上 $\rm dfs$，求 $\rm fa[v]$，$\rm dep[v]$，$\rm siz[v]$ 和 $\rm hson[v]$
第一次 $\rm dfs$：重边优先遍历，重点求 $\rm top[v]$，$\rm dfn[v]$ 和 $\rm rnk[v]$

例题：【模板】轻重链剖分/树链剖分

算法分析

我们分析一下这题的矛盾所在：

• dfs序 能高效处理子树操作，却无法直接处理路径操作
• 而且同时存在路径修改和路径查询，我们也无法通过各种技巧规避路径操作
• 而能够高效地处理路径操作的树链剖分，却无法高效处理子树操作

为什么 dfs序 无法高效处理路径操作？

• 因为一条连续的路径，对应到 dfs序 中不一定是连续的，而且也做不到始终连续。

为什么不可能做到始终连续？

• 因为如果某个节点有多个孩子，dfs序 显然只能排其中一个孩子在这个节点的下一个位置，这样到其他孩子的路径就不连续了。
• 也就是说，对每个节点，dfs序 能且只能保证每个节点向下的一条路径是连续的。我们付出的代价是和询问路径被分割成的“连续路径”的个数成正比的。
• 换言之，对每个节点，我们可以在其连向孩子的边中，选择一条边。然后，我们选中的边组成了很多链在 dfs序 中是连续的。
• 我们的操作代价与路径中包含的“链”的个数成正比

这个定义和树链剖分的定义一模一样！

于是，我们树链剖分的策略，把“重边”作为我们选择的边。也就是，在求 dfs序 中，优先 $\rm dfs$ 重边，然后再 $\rm dfs$ 轻边。

此时树剖中的每条重链，在 dfs 序中都是有序的连续的一段

由于任意一条路径都只会经过不超过 $O(\log n)$ 条重链，因此它们在 dfs序 中只会对应不超过 $O(\log n)$ 个连续区间，也就是 $O(\log^2 n)$ 个线段树节点。

通过这个巧妙的处理，我们的 dfs序 也能支持链操作了。

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 1; i <= (n); ++i)

using std::cin;
using std::cout;
using std::vector;
using ll = long long;

const int MX = 100005;
vector<int> to[MX];
int n, mod;
int a[MX];
int dep[MX], fa[MX], hson[MX], siz[MX];

void dfs1(int v) {
    siz[v] = 1;

    for (int u : to[v]) {
        if (u == fa[v]) continue;
        dep[u] = dep[v] + 1;
        fa[u] = v;
        dfs1(u);
        siz[v] += siz[u];

        if (siz[u] > siz[hson[v]]) {
            hson[v] = u;
        } 
    }
}

int pre[MX], idx;
int rnk[MX];
int top[MX];

void dfs2(int v, int x) {
    pre[v] = ++idx;
    rnk[idx] = v;
    top[v] = x;

    if (!hson[v]) return;
    dfs2(hson[v], x);

    for (int u : to[v]) {
        if (u == fa[v] or u == hson[v]) continue;
        dfs2(u, u);
    }
}

ll sum[MX * 4];
ll tag[MX * 4];

inline ll lc(ll p) { return p << 1; }

inline ll rc(ll p) { return p << 1 | 1; }

void pushUp(ll p) {
    sum[p] = sum[lc(p)] + sum[rc(p)];
}

void buildTree(ll p, ll l, ll r) {
    if (l == r) {
        sum[p] = a[rnk[l]];
        return;
    }
    ll mid = (l + r) >> 1;
    buildTree(lc(p), l, mid);
    buildTree(rc(p), mid + 1, r);
    pushUp(p);
}

void moveTag(ll p, ll l, ll r, ll t) {
    (sum[p] += t * (r - l + 1)) % mod;
    (tag[p] += t) % mod;
}

void pushDown(ll p, ll l, ll r) {
    ll mid = (l + r) >> 1;
    moveTag(lc(p), l, mid, tag[p]); 
    moveTag(rc(p), mid + 1, r, tag[p]);
    tag[p] = 0;
}

void update(ll p, ll l, ll r, ll ql, ll qr, ll d) {
    if (ql <= l && r <= qr) { 
        sum[p] += d * (r - l + 1);
        tag[p] += d;
        return;
    }
    pushDown(p, l, r);
    ll mid = (l + r) >> 1;
    if (ql <= mid) {
        update(lc(p), l, mid, ql, qr, d);
    } 
    if (mid < qr) {
        update(rc(p), mid + 1, r, ql, qr, d);
    }
    pushUp(p);
}

ll query(ll p, ll l, ll r, ll ql, ll qr) {
    if (ql <= l && r <= qr) return sum[p];
    pushDown(p, l, r);
    ll mid = (l + r) >> 1;
    ll res = 0;
    if (ql <= mid) {
        res += query(lc(p), l, mid, ql, qr);
    }
    if (mid < qr) {
        res += query(rc(p), mid + 1, r, ql, qr);
    }
    return res%mod;
}

int qTree(int u) {
    return query(1, 1, n, pre[u], pre[u] + siz[u] - 1);
}

void updTree(int u, int dx) {
    update(1, 1, n, pre[u], pre[u] + siz[u] - 1, dx);
}

int qPath(int u, int v) {
    int ans = 0;
    while (top[u] != top[v]) {
        if (dep[top[u]] < dep[top[v]]) std::swap(u, v);
        ans = (ans + query(1, 1, n, pre[top[u]], pre[u])) % mod;
        u = fa[top[u]];
    }

    if (dep[u] > dep[v]) std::swap(u, v);
    ans = (ans + query(1, 1, n, pre[u], pre[v])) % mod;
    return ans;
}

void updPath(int u, int v, int dx) {
    while (top[u] != top[v]) {
        if (dep[top[u]] < dep[top[v]]) std::swap(u, v);
        update(1, 1, n, pre[top[u]], pre[u], dx);
        u = fa[top[u]];
    }

    if (dep[u] > dep[v]) std::swap(u, v);
    update(1, 1, n, pre[u], pre[v], dx);
}

int main() {
    std::ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int m, r;
    cin >> n >> m >> r >> mod;
    rep(i, n) cin >> a[i];
    rep(i, n-1) {
        int x, y;
        cin >> x >> y;
        to[x].push_back(y);
        to[y].push_back(x);
    }

    dfs1(r);
    dfs2(r, r);

    buildTree(1, 1, n);

    while (m--) {
        int type;
        cin >> type;
        if (type == 1) {
            int x, y, z;
            cin >> x >> y >> z;
            updPath(x, y, z);
        }
        else if (type == 2) {
            int x, y;
            cin >> x >> y;
            cout << qPath(x, y) << '\n';
        }
        else if (type == 3) {
            int x, z;
            cin >> x >> z;
            updTree(x, z);
        }
        else {
            int x;
            cin >> x;
            cout << qTree(x) << '\n';
        }
    }

    return 0;
}

例2： 【模板】最近公共祖先（LCA）

查询 $\rm LCA$ 也可以用树剖来做，时间复杂度和倍增一样都是 $O(\log n)$，但常数小一些

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 1; i <= (n); ++i)

using std::cin;
using std::cout;
using std::vector;
using ll = long long;

const int MX = 500005;
vector<int> to[MX];
int n, mod;
int a[MX];
int dep[MX], fa[MX], hson[MX], siz[MX];

void dfs1(int v) {
    siz[v] = 1;

    for (int u : to[v]) {
        if (u == fa[v]) continue;
        dep[u] = dep[v] + 1;
        fa[u] = v;
        dfs1(u);
        siz[v] += siz[u];

        if (siz[u] > siz[hson[v]]) {
            hson[v] = u;
        } 
    }
}

int pre[MX], idx;
int rnk[MX];
int top[MX];

void dfs2(int v, int x) {
    pre[v] = ++idx;
    rnk[idx] = v;
    top[v] = x;

    if (!hson[v]) return;
    dfs2(hson[v], x);

    for (int u : to[v]) {
        if (u == fa[v] or u == hson[v]) continue;
        dfs2(u, u);
    }
}

int lca(int u, int v) {
    while (top[u] != top[v]) {
        if (dep[top[u]] < dep[top[v]]) std::swap(u, v);
        u = fa[top[u]];
    }

    if (dep[u] > dep[v]) std::swap(u, v);
    return u;
}

int main() {
    std::ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int m, r;
    cin >> n >> m >> r;

    rep(i, n-1) {
        int x, y;
        cin >> x >> y;
        to[x].push_back(y);
        to[y].push_back(x);
    }

    dfs1(r);
    dfs2(r, r);

    while (m--) {
        int a, b;
        cin >> a >> b;
        cout << lca(a, b) << '\n';
    }

    return 0;
}

例题3： [ZJOI2008]树的统计

树剖板题

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 1; i <= (n); ++i)

using std::cin;
using std::cout;
using std::max;
using std::vector;
using std::string;
using ll = long long;

const int MX = 30005;
vector<int> to[MX];
int n;
int a[MX], w[MX];
int dep[MX], fa[MX], hson[MX], siz[MX];

void dfs1(int v) {
    siz[v] = 1;

    for (int u : to[v]) {
        if (u == fa[v]) continue;
        dep[u] = dep[v] + 1;
        fa[u] = v;
        dfs1(u);
        siz[v] += siz[u];

        if (siz[u] > siz[hson[v]]) {
            hson[v] = u;
        } 
    }
}

int pre[MX], idx;
int rnk[MX];
int top[MX];

void dfs2(int v, int x) {
    pre[v] = ++idx;
    rnk[idx] = v;
    top[v] = x;

    if (!hson[v]) return;
    dfs2(hson[v], x);

    for (int u : to[v]) {
        if (u == fa[v] or u == hson[v]) continue;
        dfs2(u, u);
    }
}

int mx[MX * 4];
ll sum[MX * 4];

inline int lc(int p) { return p << 1; }

inline int rc(int p) { return p << 1 | 1; }

void pushUp(int p) {
    mx[p] = max(mx[lc(p)], mx[rc(p)]);
    sum[p] = sum[lc(p)] + sum[rc(p)];
}

void buildTree(int p=1, int l=1, int r=n) {
    if (l == r) {
        mx[p] = sum[p] = a[rnk[l]];
        return;
    }
    int mid = (l + r) >> 1;
    buildTree(lc(p), l, mid);
    buildTree(rc(p), mid + 1, r);
    pushUp(p);
}

void update(int q, int d, int p=1, int l=1, int r=n) {
    if (l == r) { 
        mx[p] = sum[p] = d;
        return;
    }

    int mid = (l + r) >> 1;
    if (q <= mid) {
        update(q, d, lc(p), l, mid);
    } 
    if (mid < q) {
        update(q, d, rc(p), mid + 1, r);
    }
    pushUp(p);
}

int query_max(int ql, int qr, int p=1, int l=1, int r=n) {
    if (ql <= l && r <= qr) return mx[p];

    int mid = (l + r) >> 1;
    int res = -INT_MAX;
    if (ql <= mid) {
        res = max(res, query_max(ql, qr, lc(p), l, mid));
    }
    if (mid < qr) {
        res = max(res, query_max(ql, qr, rc(p), mid + 1, r));
    }
    return res;
}

int qPath_max(int u, int v) {
    int ans = -INT_MAX;
    while (top[u] != top[v]) {
        if (dep[top[u]] < dep[top[v]]) std::swap(u, v);
        ans = max(ans, query_max(pre[top[u]], pre[u]));
        u = fa[top[u]];
    }

    if (dep[u] > dep[v]) std::swap(u, v);
    ans = max(ans, query_max(pre[u], pre[v]));
    return ans;
}

ll query_sum(int ql, int qr, int p=1, int l=1, int r=n) {
    if (ql <= l && r <= qr) return sum[p];

    int mid = (l + r) >> 1;
    ll res = 0;
    if (ql <= mid) {
        res += query_sum(ql, qr, lc(p), l, mid);
    }
    if (mid < qr) {
        res += query_sum(ql, qr, rc(p), mid + 1, r);
    }
    return res;
}

int qPath_sum(int u, int v) {
    ll ans = 0;
    while (top[u] != top[v]) {
        if (dep[top[u]] < dep[top[v]]) std::swap(u, v);
        ans += query_sum(pre[top[u]], pre[u]);
        u = fa[top[u]];
    }

    if (dep[u] > dep[v]) std::swap(u, v);
    ans += query_sum(pre[u], pre[v]);
    return ans;
}

int main() {
    std::ios::sync_with_stdio(false);
    cin.tie(nullptr);

    memset(mx, -0x3f, sizeof mx);
    cin >> n;
    rep(i, n-1) {
        int x, y;
        cin >> x >> y;
        to[x].push_back(y);
        to[y].push_back(x);
    }
    rep(i, n) cin >> a[i];

    dfs1(1);
    dfs2(1, 1);

    buildTree();

    int q;
    cin >> q;
    rep(qi, q) {
        string type;
        cin >> type;
        if (type == "CHANGE") {
            int u, t;
            cin >> u >> t;
            update(pre[u], t);
        }
        else if (type == "QMAX") {
            int u, v;
            cin >> u >> v;
            cout << qPath_max(u, v) << '\n';
        } 
        else {
            int u, v;
            cin >> u >> v;
            cout << qPath_sum(u, v) << '\n';
        }
    }

    return 0;
}

例题4： [NOI2015] 软件包管理器

题意：

给出软件包的树形依赖关系，对于每次询问，如果是安装软件，则要安装它的所有依赖软件包，如果是卸载软件，则要卸载所有依赖它的软件包。求出每次操作后改变状态的软件包的数目。

分析：

对于每个软件包，用 $1$ 代表安装了，$0$ 代表没有安装。对于安装软件，要它的所有依赖软件包都安装，也就是该节点到根节点的所有节点的值都要设为 $1$；对于卸载软件要依赖它的所有软件包都被卸载，也就是以这个节点为子树的所有节点的值都要设为 $0$。要得到题目中询问的改变状态的软件数目就只要比较前后查询出来的值的变化量即可。

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using std::cin;
using std::cout;
using std::vector;
using std::string;

const int MX = 100005;
vector<int> to[MX];
int n;
int dep[MX], fa[MX], hson[MX], siz[MX];

void dfs1(int v) {
    siz[v] = 1;

    for (int u : to[v]) {
        if (u == fa[v]) continue;
        dep[u] = dep[v] + 1;
        fa[u] = v;
        dfs1(u);
        siz[v] += siz[u];

        if (siz[u] > siz[hson[v]]) {
            hson[v] = u;
        } 
    }
}

int pre[MX], idx;
int rnk[MX];
int top[MX];

void dfs2(int v, int x) {
    pre[v] = ++idx;
    rnk[idx] = v;
    top[v] = x;

    if (!hson[v]) return;
    dfs2(hson[v], x);

    for (int u : to[v]) {
        if (u == fa[v] or u == hson[v]) continue;
        dfs2(u, u);
    }
}

int sum[MX * 4];
int tag[MX * 4];

inline int lc(int p) { return p << 1; }
inline int rc(int p) { return p << 1 | 1; }

void pushUp(int p) {
    sum[p] = sum[lc(p)] + sum[rc(p)];
}

void moveTag(int p, int l, int r, int t) {
    tag[p] = t;
    if (t == 1) {
        sum[p] = r - l + 1;
    }
    else {
        sum[p] = 0;
    }
}

void pushDown(int p, int l, int r) {
    if (tag[p] != 0) {
        int mid = (l + r) >> 1;
        moveTag(lc(p), l, mid, tag[p]);
        moveTag(rc(p), mid + 1, r, tag[p]);
        tag[p] = 0;
    }
}

void install(int p, int l, int r, int ql, int qr) {
    if (ql <= l and r <= qr) { 
        sum[p] = r - l + 1; 
        tag[p] = 1;
        return;
    }

    pushDown(p, l, r);

    int mid = (l + r) >> 1;
    if (ql <= mid) {
        install(lc(p), l, mid, ql, qr);
    } 
    if (mid < qr) {
        install(rc(p), mid + 1, r, ql, qr);
    }
    pushUp(p);
}

void remove(int p, int l, int r, int ql, int qr) {
    if (ql <= l and r <= qr) {
        sum[p] = 0;
        tag[p] = 2;
        return;
    }
    pushDown(p, l, r);
    int mid = (l + r) >> 1;
    if (ql <= mid) {
        remove(lc(p), l, mid, ql, qr);
    }
    if (mid < qr) {
        remove(rc(p), mid + 1, r, ql, qr);
    }
    pushUp(p);
}

// 安装 x 号软件包
int install(int x) {
    int past = sum[1];
    while (x != 0) {
        install(1, 1, n, pre[top[x]], pre[x]);
        x = fa[top[x]];
    }
    return sum[1] - past;
} 

// 卸载 x 号软件包
int remove(int x) {
    int past = sum[1];
    remove(1, 1, n, pre[x], pre[x] + siz[x] - 1);
    return past - sum[1];
} 

int main() {
    std::ios::sync_with_stdio(false);
    cin.tie(nullptr);

    cin >> n;
    for (int i = 2; i <= n; ++i) {
        int x;
        cin >> x;
        ++x;
        to[x].push_back(i);
    }

    dfs1(1);
    dfs2(1, 1);

    int q;
    cin >> q;
    rep(qi, q) {
        char op[20];
        int x;
        cin >> op >> x;
        ++x;
        if (op[0] == 'i') {
            cout << install(x) << '\n';
        }
        else {
            cout << remove(x) << '\n';
        }
    }

    return 0;
}

三、树上启发式合并 dsu on tree

dsu on tree 是一种处理树上不带修改的离线子树的算法，时间复杂度为 $O(\log n)$

注意某些问题不太有必要上 dsu on tree，比如子树元素和，子树元素最大值等（可合并区间信息）
不可合并区间信息：比如子树众数，子树元素种类数

dsu 其实是并查集的意思
但并不是“树上并查集”
有一种并查集的合并方式叫做“启发式合并”
启发式算法就是人们平时根据自己的经验受到启发想出来的东西
一般把小的集合往大的集合上合并就不会增加查询的路线长度
所以，并查集的启发式合并是这样做的：把小的集合往大的集合上合并
注意，和按秩合并不同，按秩合并是集合树的高度
dsu on tree 其实也是小的往大的上合并的思想

我们如何才能在一颗树上分出我们说的大小呢？
我们可以把每个节点的所有的轻儿子往重儿子上合并

dsu on tree 的流程很简洁，对于节点 $u$：

• 处理好所有轻儿子及其子树的答案，算好答案后删除刚刚算出来的轻儿子子树信息对节点 $u$ 的贡献