3.4 补码一位乘法
一、补码一位乘法
设$[X]_补 = X_0X_1X_2…X_n, [Y]_补 = Y_0Y_1Y_2…Y_n$
可以证明: (证明以后补QAQ)
$ [X * Y]_补 = [X]_补 * (0.Y_1Y_2…Y_n) - Y_0 * [X]_补 $
展开合并后有:
$ [X ∗ Y]_补 = [X]_补 ∗ ∑(Y_{n+1}−Y_n) * 2^{-n} $ (对补码乘法来说,符号位参加运算,这区别于原码一位乘法)
看求和中的括号部分,也就是说我们到底是加上$X_补$还是减又或者是$0$,就看相邻两位的差值;
因为乘数寄存器每一次操作也会右移(将相邻的两位变为倒数第一位和倒数第二位),这样也就是看倒数第二位的值于倒数第一位的差值。
也就是说:
在遵循原码乘法的规则上,对部分积的加减做处理
1、$Yn=Yn+1$ ,那么部分积加上零($0*[X]_补$当然是零啦),再右移一位
2、$Yn <Yn+1(01) $,部分积加上$[x]_补$,再右移一位
3、$Yn >Yn+1(10) $,部分积加上$[-x]_补$,再右移一位
可以发现,补码乘法涉及对$0、[x]_补、[-x]_补$三个数的运算
注意事项:
1、对于第一次运算$i = n$时,$Y_{n+1} = 0$
2、由于会有$Y_{n+1}$,所以在乘数寄存器$Y$后需要增加一位
3、每次计算乘数寄存器和部分积均右移(在乘数寄存器中是逻辑右移,而在部分积中是算术右移, 注意区分算术右移和逻辑右移的区别)
例如:
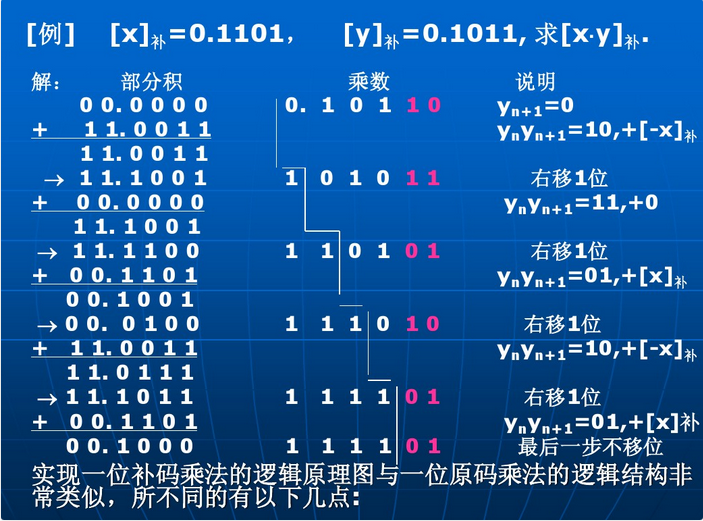
图中的部分积使用双符号位表示,部分积的结果会移动到乘数寄存器中;


学长加油!!!!!!!!!!!!
谢学弟❤️
高产啊大佬😻
东西好多,被迫高产QAQ
皮特佬牛逼
谢谢蓬蒿人❤️