目录传送门

3.5 乘法运算器设计

一、原码一位乘法器设计

图示流程图为原码乘法的步骤：

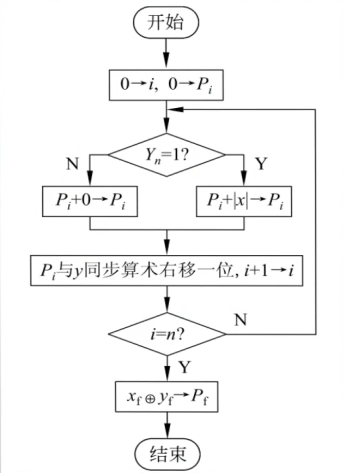
将该流程图转化为可实现的原码乘法器：

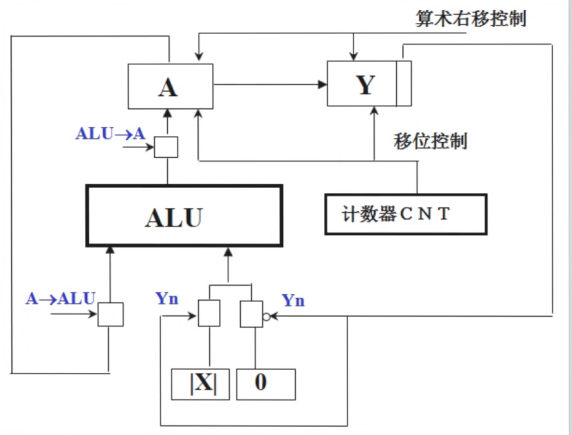
图示解析：

$ALU$是执行累加功能的加法器；

$Y$是乘数寄存器， $A$为部分积寄存器；

每次累加的对象有两个，要么为$0$，要么为$|X|$, 由乘数寄存器相关位控制；（当$Y_n$为$1$，则累加$|X|$;$Y_n$为$0$，则累加$0$）

由于原理是通过累加将乘法变为加法的，因此$A$有一个连回$ALU$的通路；

$ALU$的结果放入$A$中需要一个控制信号（图中的$ALU->A$）, 而A中的结果放回$ALU$需要另一个信号（图中的$A->ALU$）；

该乘法器需要循环累加得到乘法结果，这样计算速度就很受限制；

二、原码整列乘法器

阵列包括与门阵列和加法阵列；

与门阵列得到了所有求和的项，加法阵列用于所有项累加；

如图所示，已经将所有要相加的项排列出来了：

$a_0b_0$就是乘积的最低项，因此可以直接输出；
而其他项则需要依靠加法（一位全加器）阵列来实现；

我们将所有需要加法的地方布置上$FA$，就得到$FA$阵列；

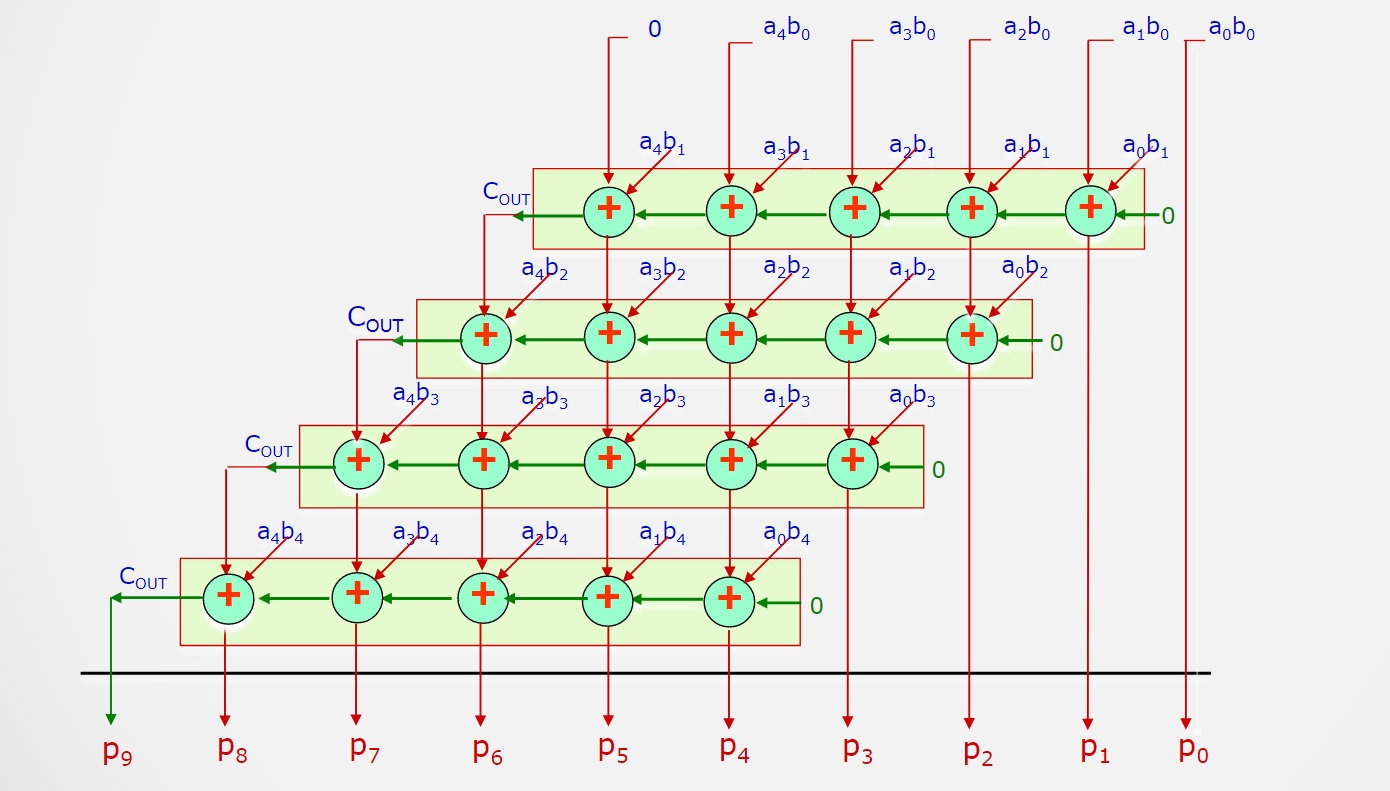
本来要在$ALU$中循环累加的乘法操作，我们通过部署大量$FA$来替代；
这样，基于硬件运算的速度，比基于循环累加的速度要快的多；

改进：

分析发现，每一行加法器都是串行进位，这对乘法器的性能影响较大；
可以通过打破串行进位链对其进行优化；

如图示：

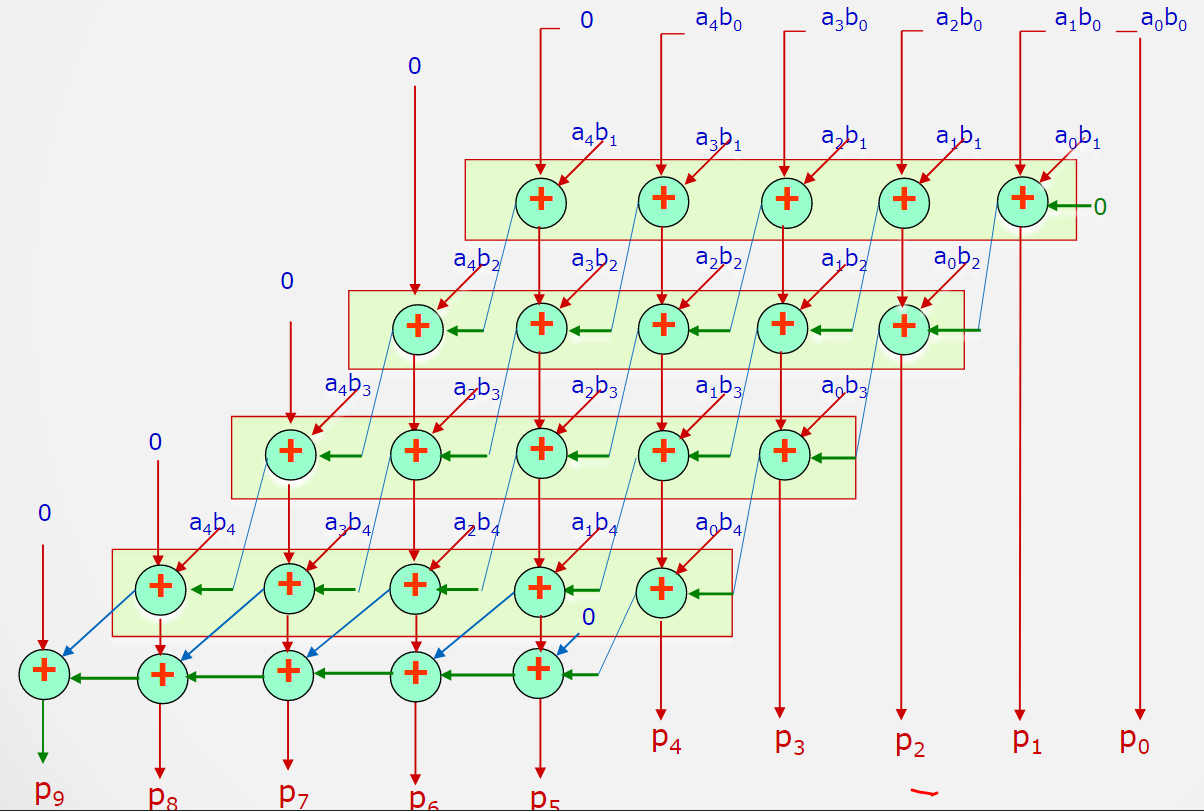
图示改进乘法器，同一行的乘法器之间不再有串行进位关系；
例如：
原本$a_0b_1$和$a_1b_0$相加的进位要送入$a_1b_1$所在加法器中，改进后直接送入$a_0b_2$所在加法器中；

由于进位本质是对下一位产生影响，因此送入加法器的不同对于结果不产生影响；
改进之后会破坏串行关系，加快运行速度，但是会出现新的进位问题，因此要多添加一行$FA$来处理原来最后一行$FA$的进位；

原码乘法规则中符号的运算是单独进行的，将符号的运算结果与数值运算结果拼起来就可以得到最后答案；

三、补码一位乘法器设计

补码乘法的规则如下：

1、$Yn=Yn+1$ ，那么部分积加上零，再右移一位

2、$Yn <Yn+1（01） $，部分积加上$[x]_补$，再右移一位

3、$Yn >Yn+1（10） $，部分积加上$[-x]_补$，再右移一位

改规则重复$n + 1$步即可得到结果；

由于补码乘法涉及对$0、[x]_补、[-x]_补$三个数的运算；
因此，基于循环累加的电路设计示意图如图示：

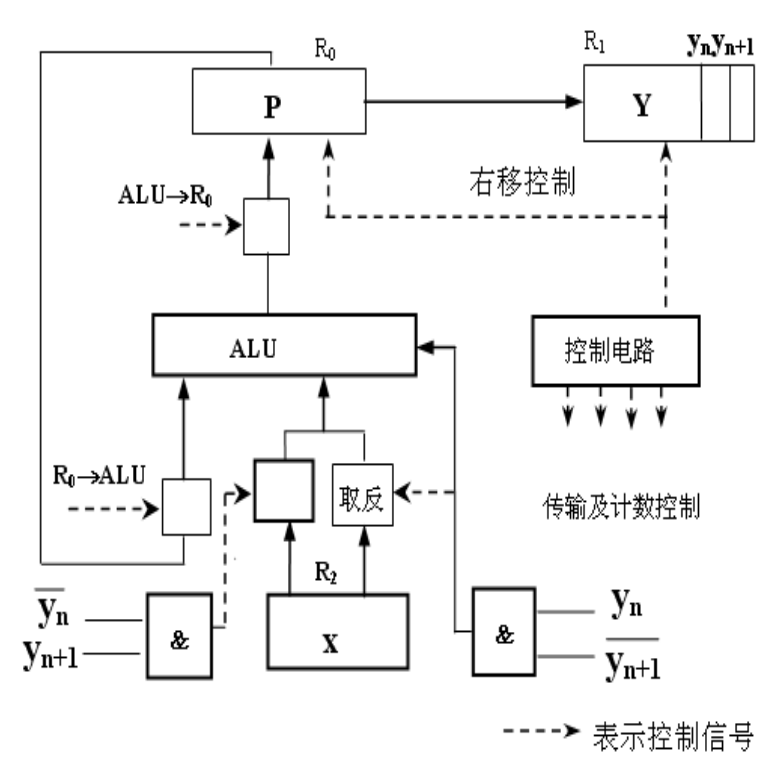
图中：

$Y$是乘数寄存器，$P$是部分积寄存器；
放入$ALU$的数据除了循环反馈的部分积之外，还有由$Y_n$和$Y_{n+1}$控制的$[X]_补$或者$[-X]_补$；
当$Y_n = Y_{n+1}$时，没有将数据送入$ALU$，这等同于加$0$；

四、补码阵列乘法器

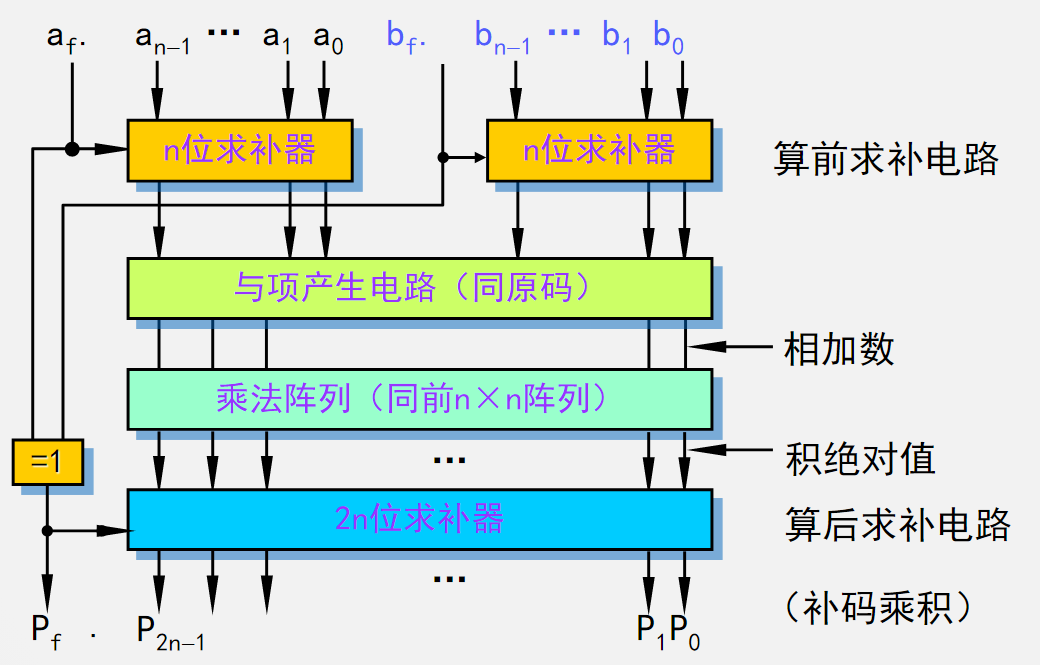
对于补码阵列乘法，以现将补码信息位其转化为原码，然后再套用原码阵列乘法器，最后再将结果求补，同样符号位单独计算；