本文章原出处:chicago01.top,转载不需说明,随意转载
例1:费解的开关
你玩过“拉灯”游戏吗?25盏灯排成一个5x5的方形。每一个灯都有一个开关,游戏者可以改变它的状态。每一步,游戏者可以改变某一个灯的状态。游戏者改变一个灯的状态会产生连锁反应:和这个灯上下左右相邻的灯也要相应地改变其状态。
[HTML_REMOVED]
我们用数字“1”表示一盏开着的灯,用数字“0”表示关着的灯。下面这种状态
10111
01101
10111
10000
11011
在改变了最左上角的灯的状态后将变成:
01111
11101
10111
10000
11011
再改变它正中间的灯后状态将变成:
01111
11001
11001
10100
11011
给定一些游戏的初始状态,编写程序判断游戏者是否可能在6步以内使所有的灯都变亮。
输入格式
第一行输入正整数n,代表数据中共有n个待解决的游戏初始状态。
以下若干行数据分为n组,每组数据有5行,每行5个字符。每组数据描述了一个游戏的初始状态。各组数据间用一个空行分隔。
输出格式
一共输出n行数据,每行有一个小于等于6的整数,它表示对于输入数据中对应的游戏状态最少需要几步才能使所有灯变亮。
对于某一个游戏初始状态,若6步以内无法使所有灯变亮,则输出“-1”。
数据范围
0<n≤500
输入样例:
3
00111
01011
10001
11010
11100
11101
11101
11110
11111
11111
01111
11111
11111
11111
11111
输出样例:
3
2
-1
题解:
#include<bits/stdc++.h>
using namespace std;
const int inf = 0x3fffffff;
char g[6][6];
int dx[6] = {0,-1,0,1,0},dy[6] = {0,0,1,0,-1};
void turn(int x,int y)
{
for(int i = 0;i < 5;++i)
{
int nx = x + dx[i],ny = y + dy[i];
if(nx >= 0 && nx < 5 && ny >= 0 && ny < 5)
g[nx][ny] ^= 1;
}
}
int work()
{
int ans = inf;
for(int i = 0;i < 1 << 5;++i)
{
int res = 0;
char cpy[6][6];
memcpy(cpy,g,sizeof(g));
for(int j = 0;j < 5;++j)
{
if(i >> j & 1)
{
res ++;
turn(0,j);
}
}
for(int y = 0;y < 4;++y)
{
for(int x = 0;x < 5;++x)
{
if(g[y][x] == '0')
{
res ++ ;
turn(y + 1,x);
}
}
}
bool qwq = true;
for(int x = 0;x < 5;++x)
if(g[4][x] == '0')
{
qwq = false;
break;
}
if(qwq) ans = min(ans,res);
memcpy(g,cpy,sizeof(g));
}
if(ans > 6) ans = -1;
return ans;
}
int main(void)
{
int T;
cin >> T;
while(T--)
{
for(int i = 0;i < 5;++i)
cin >> g[i];
cout << work() << endl;
}
return 0;
}
例2:奇怪的汉诺塔
汉诺塔问题,条件如下:
1、这里有A、B、C和D四座塔。
2、这里有n个圆盘,n的数量是恒定的。
3、每个圆盘的尺寸都不相同。
4、所有的圆盘在开始时都堆叠在塔A上,且圆盘尺寸从塔顶到塔底逐渐增大。
5、我们需要将所有的圆盘都从塔A转移到塔D上。
6、每次可以移动一个圆盘,当塔为空塔或者塔顶圆盘尺寸大于被移动圆盘时,可将圆盘移至这座塔上。
请你求出将所有圆盘从塔A移动到塔D,所需的最小移动次数是多少。
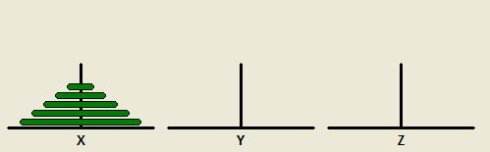
汉诺塔塔参考模型
输入格式
没有输入
输出格式
对于每一个整数n(1≤n≤12),输出一个满足条件的最小移动次数,每个结果占一行。
输入样例:
没有输入
输出样例:
参考输出格式
#### 题解:
先看图:
- 三柱两盘的情况(刨去初时状态,共移动了3次)

- 三柱三盘的情况(刨去初时状态,共移动了7次)

综上两图,我们可以看到,对于n盘3塔问题,移动的最小步数就是,把前n-1个盘子从A柱移到B柱,然后把第n个盘子移到C柱,最后再把前n-1个盘子移动到C柱。可以得出递推式d[n]=d[n−1]∗2+1 。
但是本题没有呢么友善,题目要求我们求四塔情况下最小的移动步数,难受死我了,呢就继续画图看看??
- 四塔3盘(除去初始状态,共移动5次)

- 四塔4盘(除去初始状态,共盘他9次)

综上,可得先把i个盘子在四塔的模式下,移动到一根柱子上(不可以是D柱),然后把n-i个盘子,盘到D柱上。考虑到i可能存在最小值,如上图⑤⑥中的C柱。可得递推式f[i]=min1≤i<n(2∗f[i]+d[n−i]),f[1]=1 。
代码献丑了。。。
#include<bits/stdc++.h>
using namespace std;
int a[15],f[15];
int main(void)
{
a[1] = 1;
for(int i = 2;i <= 12;++i)
a[i] = 1 + a[i-1] * 2;
memset(f,0x3f,sizeof(f));
f[0] = 0;
for(int i = 1;i <= 12;++i)
{
for(int j = 0;j < i;++j)
f[i] = min(f[i],f[j] * 2 + a[i - j]);
}
for(int i = 1;i <= 12;++i)
cout << f[i] << endl;
return 0;
}

