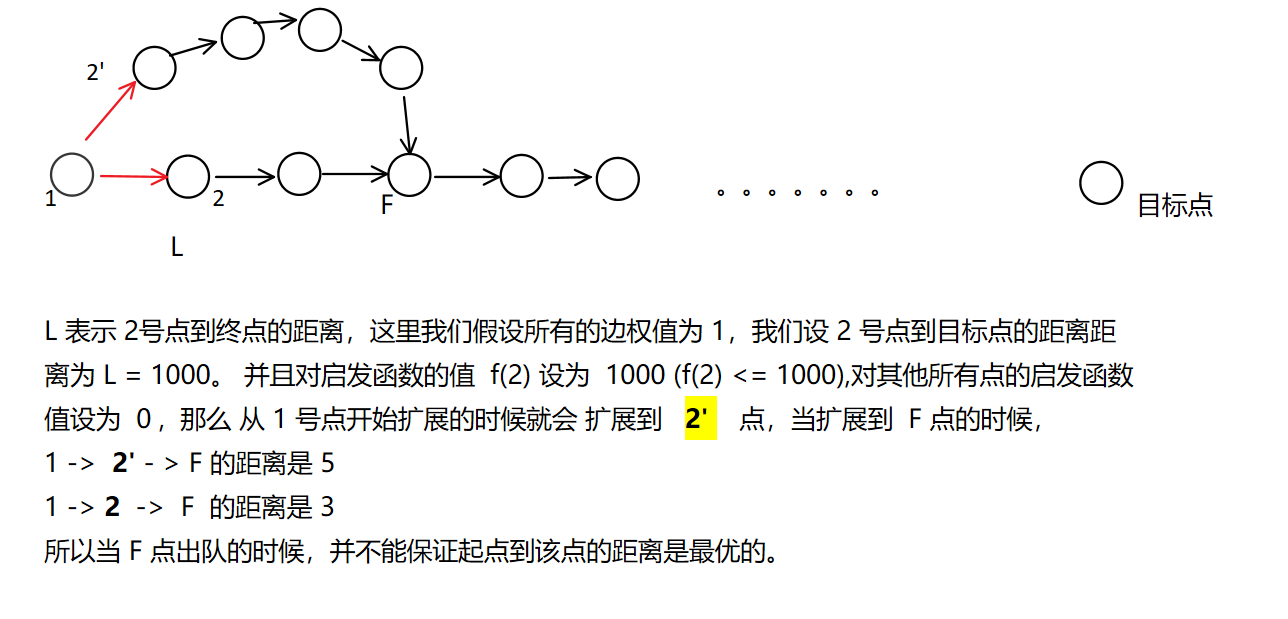
A* 算法

优先队列BFS的缺陷

在最短路问题中，如果所有边权值都是非负的，并且这个问题有解。那么就可以 通过 启发函数 来优化 BFS

对比 Dijkstra 算法来说，Dijstra 算法是没有“启发函数”的加持，就与优化队列BFS有一样的局限性
而 A* 算法会 根据 “启发函数值” + 当前距离值 进行搜索。

该启发函数， 会以任意 “状态”作为输入，计算从该状态到目标状态所需代价的估计值。
在搜索中，仍然维护一个堆，不断从中取出 “当前代价 + 未来估计（启发函数的值）”最小状态进行扩展

启发函数的基本准则

​ —— 为保证第一次从堆中取出目标状态时达到最优解。

设当前状态 state 到目标状态所需代价的估计值为 f(state).
设在未来的搜索算法中，实际求出的从当前状态 state 到目标状态的最小代价为 g(state)

对于任意的 state ， 应该有  f(state) <=  g(state)

即：启发函数的值（估价）不能大于未来实际代价，估价比实际代价更优。
这个基本准则为什么成立 ？



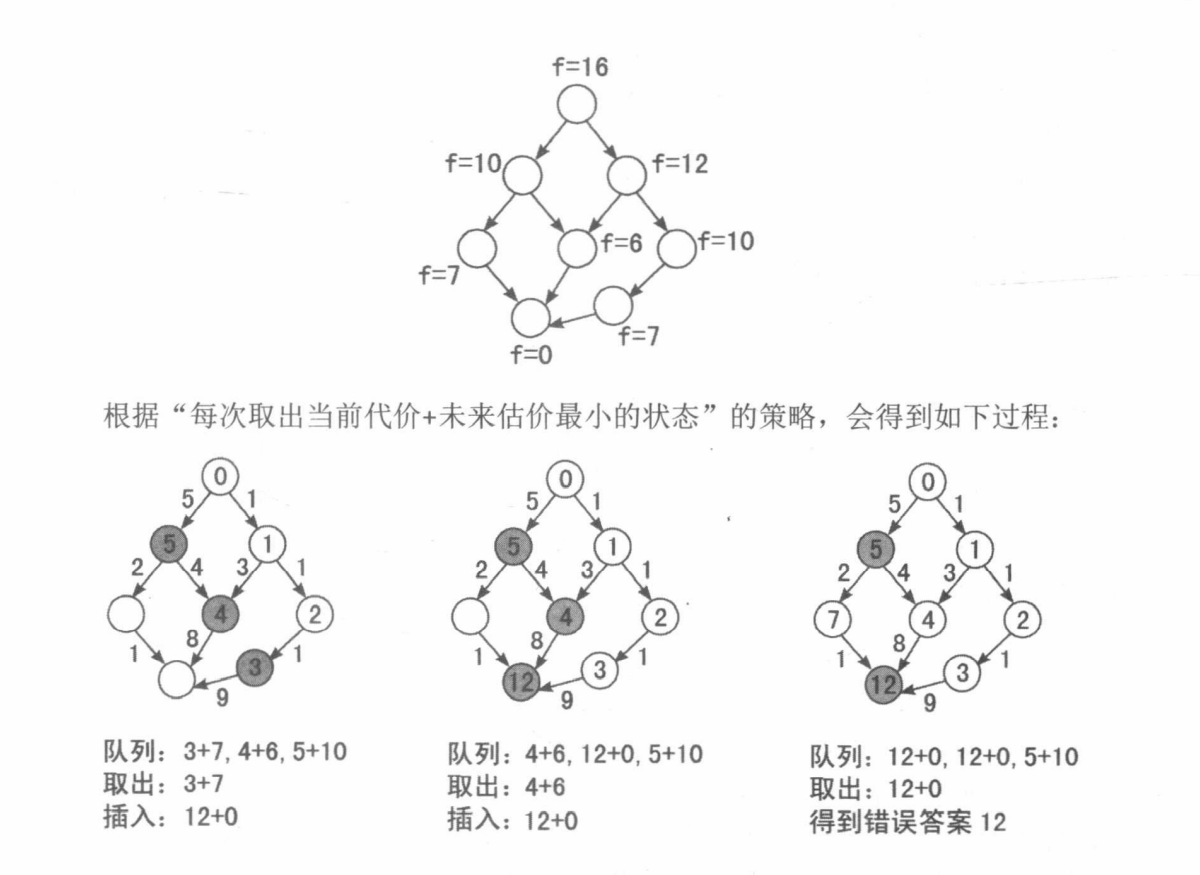
A* 算法只能保证 在终点出队之后，到终点的距离是最优的，并不能保证在中间某个状态下是最优的，并且每个点不是只被 扩展一次。