AcWing 785. 快速排序
快速排序本质上是分治法
- 分解成子问题
- 递归处理子问题
- 合并子问题
#include<iostream>
using namespace std;
const int N = 1e6 + 10;
int n;
int q[N];
void quick_sort(int q[], int l, int r)
{
//递归的边界情况,到这个时候子问题不能继续分解
if(l >= r) return;
//分解为子问题
int x = q[(l + r) >> 1], i = l - 1, j = r + 1;
while(i < j)
{
do i ++ ; while(q[i] < x);
do j -- ; while(q[j] > x);
if(i < j) swap(q[i], q[j]);
}
//递归处理子问题
quick_sort(q, l, j);
quick_sort(q, j + 1, r);
}
int main()
{
scanf("%d", &n);
for(int i = 0; i < n; i ++ ) scanf("%d", &q[i]);
quick_sort(q, 0, n - 1);
for(int i = 0; i < n; i ++ ) printf("%d ", q[i]);
return 0;
}
AcWing 786. 第k个数
减治法,分治法的一种形式
每次只需要判断k在左区间还是右区间,一直递归查找k所在区间,另外的一个区间则舍去
最后只剩一个数时,只会有数组[k]一个数,返回数组[k]的值就是答案
#include<iostream>
using namespace std;
const int N = 1e5 + 10;
int n, k;
int q[N];
int quick_sort(int l, int r, int k)
{
if(l == r) return q[l];
int x = q[l], i = l - 1, j = r + 1;
while(i < j)
{
while(q[ ++ i] < x);
while(q[ -- j] > x);
if(i < j) swap(q[i], q[j]);
}
//判断k所在的区间,sl表示左区间的长度
int sl = j - l + 1;
//k在左区间
if(k <= sl) return quick_sort(l, j, k);
//k在右区间,k - sl表示 k 在右区间的位置
else return quick_sort(j + 1, r, k - sl);
}
int main()
{
cin >> n >> k;
for(int i = 0; i < n; i ++ ) cin >> q[i];
cout << quick_sort(0, n - 1, k) << endl;
return 0;
}
AcWing 787. 归并排序
分治法的典型
- 分解成子问题
- 递归处理子问题
- 合并子问题

#include<iostream>
using namespace std;
const int N = 1e6 + 10;
int n;
int q[N], tmp[N]; //tmp作为辅助数组
void merge_sort(int q[], int l, int r)
{
//子问题不能再接着分解了
if(l >= r) return;
//分解子问题
int mid = l + r >> 1;
merge_sort(q, l, mid);
merge_sort(q, mid + 1, r);
//合并子问题
int k = 0, i = l, j = mid + 1;
while(i <= mid && j <= r)
{
if(q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];
else tmp[k ++ ] = q[j ++ ];
}
while(i <= mid) tmp[k ++ ] = q[i ++ ];
while(j <= r) tmp[k ++ ] = q[j ++ ];
for(i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];
}
int main()
{
scanf("%d", &n);
for(int i = 0; i < n; i ++ ) scanf("%d", &q[i]);
merge_sort(q, 0, n - 1);
for(int i = 0; i < n; i ++ ) printf("%d ", q[i]);
return 0;
}
AcWing 788. 逆序对的数量
#include<iostream>
using namespace std;
typedef long long LL;
const int N = 1e6 + 10;
int n;
int q[N], tmp[N];
LL merge_sort(int l, int r)
{
if(l >= r) return 0;
int mid = l + r >> 1;
LL res = merge_sort(l, mid) + merge_sort(mid + 1, r);
int k = 0, i = l, j = mid + 1;
while(i <= mid && j <= r)
if(q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];
else
{
tmp[k ++ ] = q[j ++ ];
res += mid - i + 1;
}
while(i <= mid) tmp[k ++ ] = q[i ++ ];
while(j <= r) tmp[k ++ ] = q[j ++ ];
for(int i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];
return res;
}
int main()
{
cin >> n;
for(int i = 0; i < n; i ++ ) cin >> q[i];
cout << merge_sort(0, n - 1) << endl;
return 0;
}
AcWing 789. 数的范围
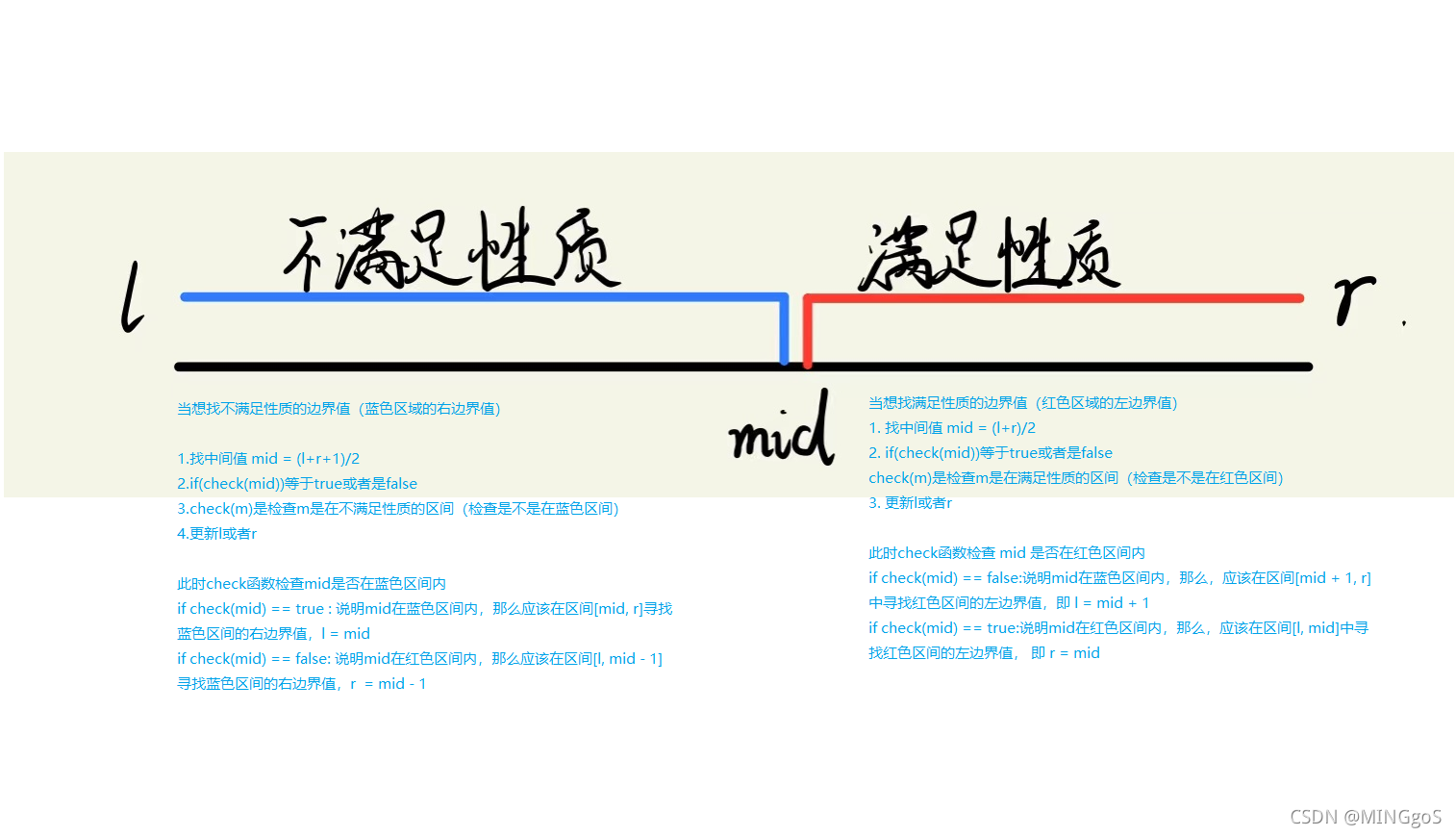
一道典型的二分法处理的题目
当想找不满足性质的边界值(蓝色区域的右边界值)
- 找中间值 mid = (l+r+1)/2
- if(check(mid))等于true或者是false
- check(m)是检查m是在不满足性质的区间(检查是不是在蓝色区间)
- 更新l或者r
此时check函数检查mid是否在蓝色区间内
if check(mid)== true :说明mid在蓝色区间内,那么应该在区间[mid, r]寻找蓝色区间的右边界值,l = mid
if check(mid)== false:说明mid在红色区间内,那么应该在区间[l, mid - 1]寻找蓝色区间的右边界值,r = mid - 1
当想找满定在质的五界值(红色区域的差边界值)
- 找中间值mid = (l+r)/2
- if(check(mid))等于true或者是false
- check(m)是检查m是在满足性质的区间(检查是不是在红色区间)
- 更新l或者r
此时check函数检查mid是否在红色区间内
if check(mid)== false:说明mid在蓝色区间内,那么,应该在区间[mid + 1, r]中寻找红色区间的左边界值,即l= mid + 1
if check(mid)== true:说明mid在红色区间内,那么,应该在区间[l, mid]中寻找红色区间的左边界值,即r = mid
#include<iostream>
using namespace std;
const int N = 1e5 + 10;
int n, m;
int q[N];
int main()
{
scanf("%d%d", &n, &m);
for(int i = 0; i < n; i ++ ) scanf("%d", &q[i]);
while(m -- )
{
int x;
scanf("%d", &x);
int l = 0, r = n - 1;
//检查左边界
while(l < r)
{
int mid = l + r >> 1;
if(q[mid] >= x) r = mid;
else l = mid + 1;
}
if(q[l] != x) cout << "-1 -1" << endl;
else
{
cout << l << " ";
int l = 0, r = n - 1;
//检查右边界
while(l < r)
{
int mid = l + r + 1 >> 1;
if(q[mid] <= x) l = mid;
else r = mid - 1;
}
cout << r << endl;
}
}
return 0;
}
AcWing 790. 数的三次方根
二分法处理问题
#include<iostream>
using namespace std;
int main()
{
double x;
cin >> x;
double l = -10000, r = 10000;
while(r - l > 1e-8)
{
double mid = (l + r) / 2;
if(mid * mid * mid >= x) r = mid;
else l = mid;
}
printf("%lf", l);
return 0;
}
AcWing 791. 高精度加法
模拟一下列竖式进行加法运算,使用一个变量carry,进行进位的操作,

#include<iostream>
#include<vector>
using namespace std;
vector<int> add(vector<int> &A, vector<int> &B)
{
vector<int> C;
int t;
for(int i = 0; i < A.size() || i < B.size(); i ++ )
{
if(i < A.size()) t += A[i];
if(i < B.size()) t += B[i];
C.push_back(t % 10);
t /= 10;
}
if(t) C.push_back(1);
return C;
}
int main()
{
string a, b;
vector<int> A, B;
cin >> a >> b;
for(int i = a.size() - 1; i >= 0; i -- ) A.push_back(a[i] - '0');
for(int i = b.size() - 1; i >= 0; i -- ) B.push_back(b[i] - '0');
auto C = add(A, B);
for(int i = C.size() - 1; i >= 0; i -- ) printf("%d", C[i]);
return 0;
}
AcWing 792. 高精度减法
#include<iostream>
#include<vector>
using namespace std;
bool cmp(vector<int> &A, vector<int> &B)
{
if(A.size() != B.size()) return A.size() > B.size();
for(int i = A.size() - 1; i >= 0; i -- )
if(A[i] != B[i])
return A[i] > B[i];
return true;
}
vector<int> sub(vector<int> &A, vector<int> &B)
{
vector<int> C;
for(int i = 0, t = 0; i < A.size(); i ++ )
{
t = A[i] - t;
if(i < B.size()) t -= B[i];
C.push_back((t + 10) % 10);
if(t < 0) t = 1;
else t = 0;
}
while(C.size() > 1 && C.back() == 0) C.pop_back();
return C;
}
int main()
{
string a, b;
vector<int> A, B;
cin >> a >> b;
for(int i = a.size() - 1; i >= 0; i -- ) A.push_back(a[i] - '0');
for(int i = b.size() - 1; i >= 0; i -- ) B.push_back(b[i] - '0');
if(cmp(A, B))
{
auto C = sub(A, B);
for(int i = C.size() - 1; i >= 0; i -- ) printf("%d", C[i]);
}
else
{
auto C = sub(B, A);
printf("-");
for(int i = C.size() - 1; i >= 0; i -- ) printf("%d", C[i]);
}
return 0;
}
AcWing 793. 高精度乘法
#include<iostream>
#include<vector>
using namespace std;
vector<int> mul(vector<int> &A, vector<int> &B)
{
vector<int> C(A.size() + B.size());
for(int i = 0; i < A.size(); i ++ )
for(int j = 0; j < B.size(); j ++ )
C[i + j] += A[i] * B[j];
for(int i = 0, t = 0; i < C.size() || t; i ++ )
{
t += C[i];
if(i >= C.size()) C.push_back(t % 10);
else C[i] = t % 10;
t /= 10;
}
while(C.size() > 1 && C.back() == 0) C.pop_back();
return C;
}
int main()
{
string a, b;
cin >> a >> b;
vector<int> A, B;
for(int i = a.size() - 1; i >= 0; i -- ) A.push_back(a[i] - '0');
for(int i = b.size() - 1; i >= 0; i -- ) B.push_back(b[i] - '0');
auto C = mul(A, B);
for(int i = C.size() - 1; i >= 0; i -- ) cout << C[i];
puts("");
return 0;
}
AcWing 794. 高精度除法
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
vector<int> div(vector<int> &A, int b, int &r)
{
vector<int> C;
r = 0;
for(int i = A.size() - 1; i >= 0; i -- )
{
r = r * 10 + A[i];
C.push_back(r / b);
r = r % b;
}
reverse(C.begin(), C.end());
while(C.size() > 1 && C.back() == 0) C.pop_back();
return C;
}
int main()
{
string a;
int b;
cin >> a >> b;
vector<int> A;
for(int i = a.size() - 1; i >= 0; i -- ) A.push_back(a[i] - '0');
int r;
auto C = div(A, b, r);
for(int i = C.size() - 1; i >= 0; i -- ) printf("%d", C[i]);
cout << endl << r << endl;
return 0;
}
AcWing 795. 前缀和
原数组: a[1], a[2], a[3], a[4], a[5], …, a[n]
前缀和:S[i] = a[1] + a[2] + a[3] + … + a[i]
作用:可以快速求出数组中某一段连续区间的和
用法:求数组a[l],a[l + 1], a[l + 2], ..., a[r]的和,即S[r] - S[l - 1]
#include<iostream>
using namespace std;
const int N = 1e5 + 10;
int n, m;
int a[N], s[N];
int main()
{
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
for(int i = 1; i <= n; i ++ ) s[i] = s[i - 1] + a[i];
while(m -- )
{
int l, r;
scanf("%d%d", &l, &r);
printf("%d\n", s[r] - s[l - 1]);
}
return 0;
}
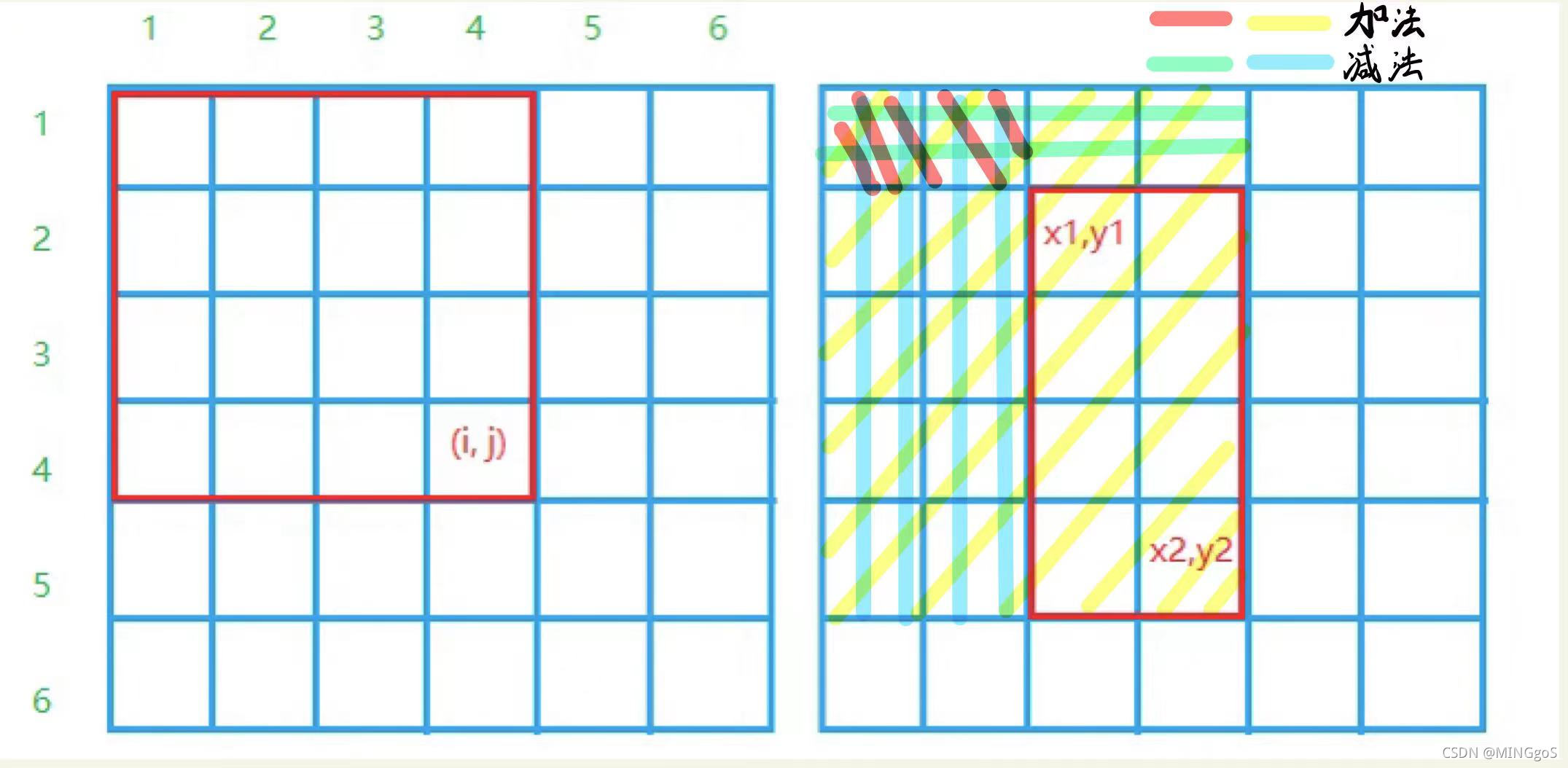
AcWing 796. 子矩阵的和
S[i, j]表示从a[1, 1] 到 a[i, j] 这个矩阵的元素的和
$S[i,j]=S[i,j−1]+S[i−1,j]−S[i−1,j−1]+a[i,j]$
(x1,y1) 到 (x2, y2)这个子矩阵的计算公式
$S[x2,y2]−S[x1−1,y2]−S[x2,y1−1]+S[x1−1,y1−1]$

#include<iostream>
using namespace std;
const int N = 1010;
int m, n, q;
int a[N][N], s[N][N];
int main()
{
scanf("%d%d%d", &n, &m, &q);
for(int i = 1; i <= n; i ++ )
for(int j = 1; j <= m; j ++ )
scanf("%d", &a[i][j]);
for(int i = 1; i <= n; i ++ )
for(int j = 1; j <= m; j ++ )
s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];
while(q -- )
{
int x1, y1, x2, y2;
scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
printf("%d\n", s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]);
}
return 0;
}
AcWing 797. 差分
首先给定一个原数组a:$a[1], a[2], a[3],,,,,, a[n];$
然后我们构造一个数组b :$b[1] ,b[2] , b[3],,,,,, b[i];$
使得 $a[i] = b[1] + b[2 ]+ b[3] +,,,,,, + b[i]$
$a[0 ]= 0;$
$b[1] = a[1] - a[0];$
$b[2] = a[2] - a[1];$
$b[3] =a [3] - a[2];$
........
$b[n] = a[n] - a[n-1];$
由公式可以得知,数组a是数组b的前缀和数组,反过来,数组b是数组a的差分数组
应用场景:
给定区间[l ,r],让我们把a数组中的[l, r]区间中的每一个数都加上c,即
$a[l] + c , a[l+1] + c , a[l+2] + c ,… , a[r] + c;$
如果单纯使用for循环去做加法,那么m次加上c的时间复杂度则为$O(n * m)$
这个时候要将时间复杂度降低就可以使用差分数组了
a数组是b数组的前缀和数组,比如对b数组的b[i]的修改,会影响到a数组中从a[i]及往后的每一个数。
首先让差分b数组中的 $b[l] + c$ ,a数组变成 $a[l] + c ,a[l+1] + c,…, a[n] + c$;
然后为了避免对数组中坐标r之后的值造成影响,$b[r+1] - c$, a数组变成 $a[r+1] - c,a[r+2] - c,…,a[n] - c$;

因此一维差分对a数组的[l, r]区间同时加上一个数c,只需要对其差分数组b,做出$b[l] += c$, $b[r + 1] -= c$ 的操作,时间复杂度为$O(1)$,m次操作的总体时间复杂度则从$O(n*m)$降低到$O(m)$
#include<iostream>
using namespace std;
const int N = 1e5 + 10;
int n, m;
int a[N], b[N];
void insert(int l, int r, int c)
{
b[l] += c;
b[r + 1] -= c;
}
int main()
{
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
for(int i = 1; i <= n; i ++ ) insert(i, i, a[i]);
while(m -- )
{
int l, r, c;
scanf("%d%d%d", &l, &r, &c);
insert(l, r, c);
}
for(int i = 1; i <= n; i ++ ) b[i] += b[i - 1];
for(int i = 1; i <= n; i ++ ) printf("%d ", b[i]);
return 0;
}
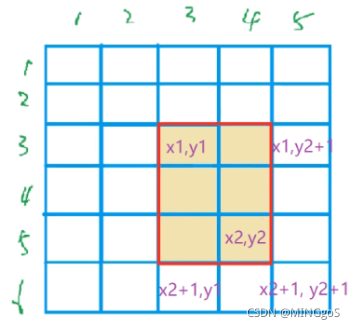
AcWing 798. 差分矩阵
与一维前缀和延伸至二维前缀和的过程类似
一维差分延伸至二维差分
核心操作:
$b[x1][y1] += c;$
$b[x2 + 1][y1] -= c;$
$b[x1][y2 + 1] -= c;$
$b[x2 + 1][y2 + 1] += c;$
#include<iostream>
using namespace std;
const int N = 1010;
int n, m, q;
int a[N][N], b[N][N];
void insert(int x1, int y1, int x2, int y2, int c)
{
b[x1][y1] += c;
b[x2 + 1][y1] -= c;
b[x1][y2 + 1] -= c;
b[x2 + 1][y2 + 1] += c;
}
int main()
{
scanf("%d%d%d", &n, &m, &q);
for(int i = 1; i <= n; i ++ )
for(int j = 1; j <= m; j ++ )
scanf("%d", &a[i][j]);
for(int i = 1; i <= n; i ++ )
for(int j = 1; j <= m; j ++ )
insert(i, j, i, j, a[i][j]);
while(q -- )
{
int x1, y1, x2, y2, c;
cin >> x1 >> y1 >> x2 >> y2 >> c;
insert(x1, y1, x2, y2, c);
}
for(int i = 1; i <= n; i ++ )
for(int j = 1; j <= m; j ++ )
b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];
for(int i = 1; i <= n; i ++ )
{
for(int j = 1; j <= m; j ++ )
printf("%d ", b[i][j]);
puts("");
}
return 0;
}
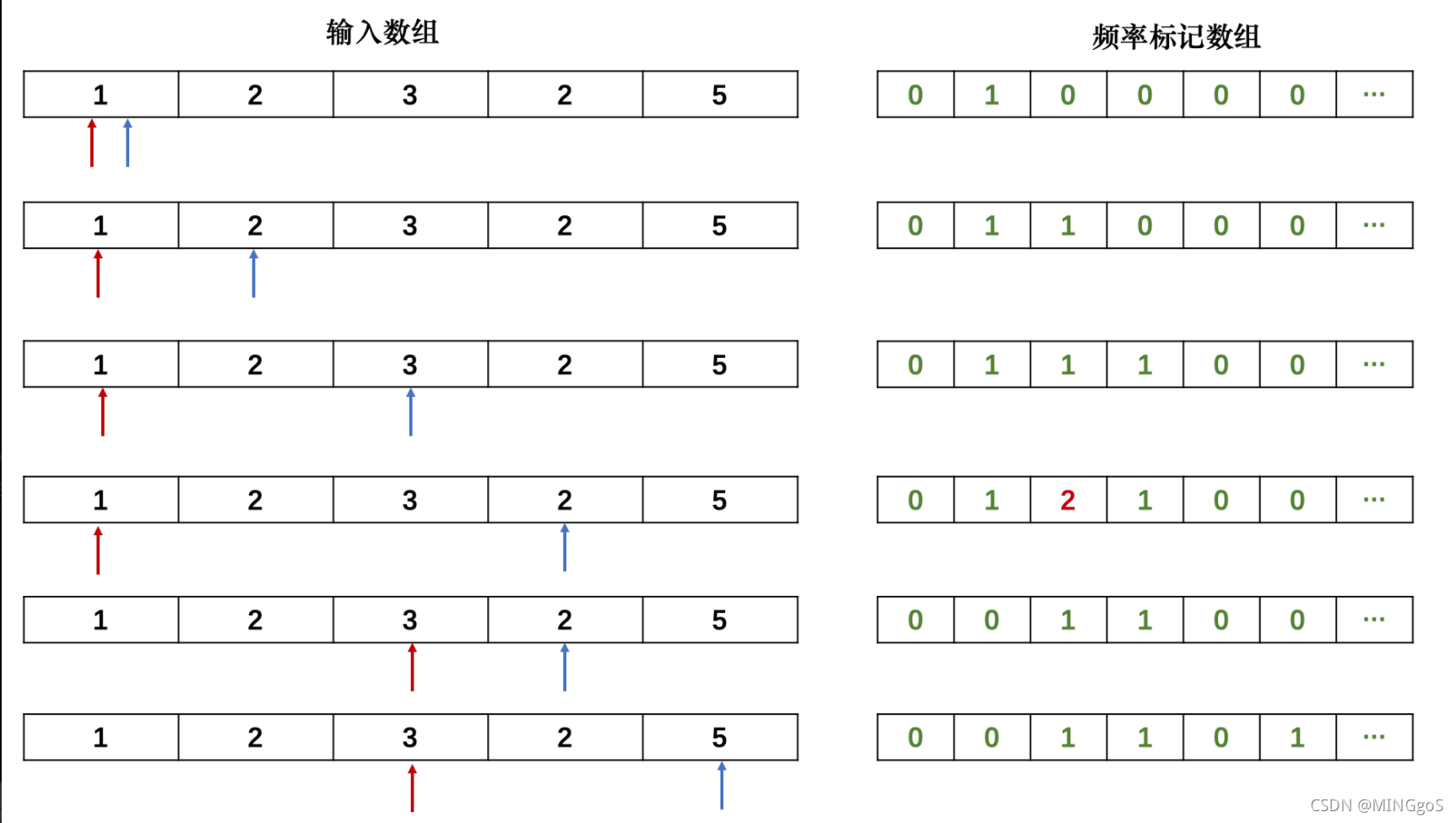
AcWing 799. 最长连续不重复子序列
双指针算法。
使用一个数组s维护当前找到的区间 [i, j]中数字的个数。
如果出现重复数字,那么指针 i 向后移动一位,并且哈希表中这个数字的出现次数减一,直到没有重复字符为止,使用了一个while循环实现
如果没有重复数组,那么指针 j 向后移动一位,同时s中对应的数字出现次数加一
在这个过程中使用res记录子序列长度的最大值。
#include<iostream>
using namespace std;
const int N = 1e6 + 10;
int a[N], s[N];
int n;
int main()
{
cin >> n;
for(int i = 0; i < n; i ++ ) cin >> a[i];
int res = 0;
for(int i = 0, j = 0; i < n; i ++ )
{
s[a[i]] ++ ;
while(s[a[i]] > 1)
{
s[a[j]] -- ;
j ++ ;
}
res = max(res, i - j + 1);
}
cout << res << endl;
return 0;
}
AcWing 800. 数组元素的目标和
i从 0开始 从前往后遍历
j从 m - 1开始 从后向前遍历,j指针不会回退
#include<iostream>
using namespace std;
const int N = 1e5 + 10;
int n, m, x;
int a[N], b[N];
int main()
{
scanf("%d%d%d", &n, &m, &x);
for(int i = 0; i < n; i ++ ) scanf("%d", &a[i]);
for(int i = 0; i < m; i ++ ) scanf("%d", &b[i]);
for(int i = 0, j = m - 1; i < n; i ++ )
{
while(j > 0 && a[i] + b[j] > x) j -- ;
if(j >= 0 && a[i] + b[j] == x)
cout << i << " " << j << endl;
}
return 0;
}
AcWing 2816. 判断子序列
j指针用来扫描整个b数组,i指针用来扫描a数组。若发现a[i]==b[j],则让i指针后移一位。- 整个过程中,
j指针不断后移,而i指针只有当匹配成功时才后移一位,若最后若i==n,则说明匹配成功。
#include<iostream>
using namespace std;
const int N = 1e5 + 10;
int n, m;
int a[N], b[N];
int main()
{
cin >> n >> m;
for(int i = 0; i < n; i ++ ) cin >> a[i];
for(int i = 0; i < m; i ++ ) cin >> b[i];
int j = 0;
for(int i = 0; i < m; i ++ )
if(b[i] == a[j])
j ++ ;
if(j == n) cout << "Yes" << endl;
else cout << "No" << endl;
return 0;
}
AcWing 801. 二进制中1的个数
按位与运算

#include<iostream>
using namespace std;
int lowBit(int x)
{
return x & -x;
}
int main()
{
int n;
cin >> n;
while(n -- )
{
int x;
cin >> x;
int res = 0;
while(x)
{
x -= lowBit(x);
res ++ ;
}
cout << res << " ";
}
return 0;
}
AcWing 802. 区间和
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
typedef pair<int, int> PII;
const int N = 3e5 + 10;
int n, m;
int a[N], s[N];
vector<int> all;
vector<PII> add, query;
int find(int x)
{
int l = 0, r = all.size() - 1;
while(l < r)
{
int mid = l + r >> 1;
if(all[mid] >= x) r = mid;
else l = mid + 1;
}
return r + 1;
}
int main()
{
cin >> n >> m;
for(int i = 0; i < n; i ++ )
{
int x, c;
cin >> x >> c;
add.push_back({x, c});
all.push_back(x);
}
for(int i = 0; i < m; i ++ )
{
int l, r;
cin >> l >> r;
query.push_back({l, r});
all.push_back(l);
all.push_back(r);
}
sort(all.begin(), all.end());
all.erase(unique(all.begin(), all.end()), all.end());
for(auto item : add)
{
int x = find(item.first);
a[x] += item.second;
}
for(int i = 1; i <= all.size(); i ++ ) s[i] = s[i - 1] + a[i];
for(auto item : query)
{
int l = find(item.first), r = find(item.second);
cout << s[r] - s[l - 1] << endl;
}
return 0;
}
AcWing 803. 区间合并
思想方法类似于贪心
- 先给每个区间按左端点排序
- 遍历每个区间
如果第二个区间起点小于第一个区间终点,那么就是有交集,将第一个区间的终点更新为第二个区间的终点
如果没有交集,那么将前面更新完毕的区间存储起来

#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
typedef pair<int, int> PII;
int n;
vector<PII> seg;
void merge(vector<PII> &Seg)
{
vector<PII> res;
int st = -2e9, ed = -2e9;
sort(Seg.begin(), Seg.end());
for(auto seg : Seg)
{
if(ed < seg.first)
{
if(ed != -2e9) res.push_back({st, ed});
st = seg.first;
ed = seg.second;
}
else ed = max(ed, seg.second);
}
if(st != -2e9) res.push_back({st, ed});
Seg = res;
}
int main()
{
cin >> n;
for(int i = 0; i < n; i ++ )
{
int l, r;
cin >> l >> r;
seg.push_back({l, r});
}
merge(seg);
cout << seg.size() << endl;
return 0;
}

