AcWing 826. 单链表

e[i]: 存放需要存入的值
ne[i]：存放下一个节点的下标
idx :记录当前的操作的位置

插入头结点
利用一个head指针记录头结点的位置

void add_to_head(int x)
{
    e[idx] = x, ne[idx] = head, head = idx ++ ;
}

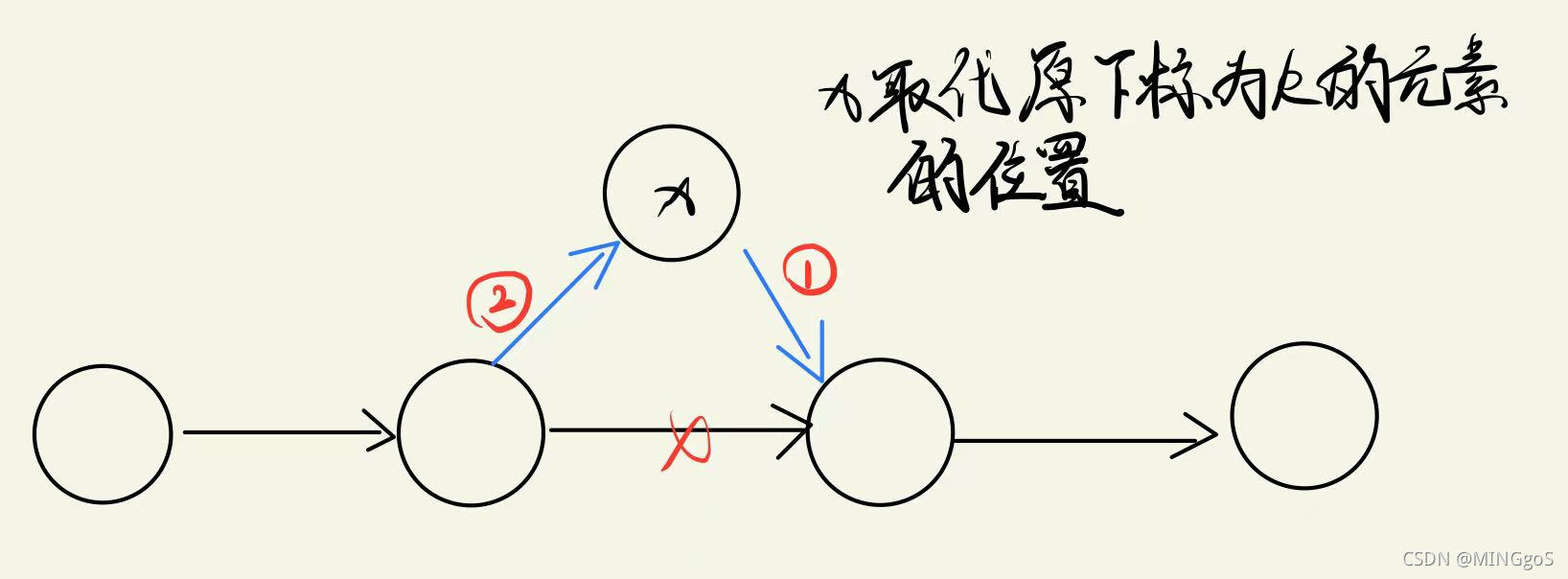
插入操作

void add(int k, int x)
{
    e[idx] = x;         //e[idx]记录新插入的节点的值
    ne[idx] = ne[k];    //新节点的next指针指向 newPoint, newPoint -> next = k -> next
    ne[k] = idx;        //原位于位置k的节点的next指针指向新节点,k -> next = newPoint
    idx ++ ;            //更新idx的值
}

①ne[idx] = ne[k];
②ne[k] = idx;

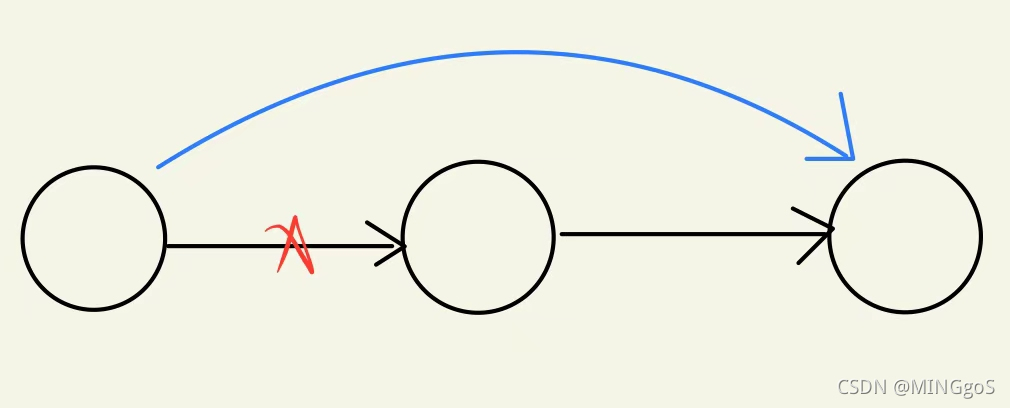
删除操作
相当于 p -> next = p -> next -> next

void remove(int k)
{
    ne[k] = ne[ne[k]];
}

#include<iostream>
using namespace std;

const int N = 1e5 + 10;
int e[N], ne[N];

int head, idx;

void init()
{
    head = -1;
    idx = 0;
}

void add_to_head(int x)
{
    e[idx] = x, ne[idx] = head, head = idx ++ ;
}

void add(int k, int x)
{
    e[idx] = x, ne[idx] = ne[k], ne[k] = idx ++ ;
}

void remove(int k)
{
    ne[k] = ne[ne[k]];
}

int main()
{
    int m;
    cin >> m;

    init();

    while(m -- )
    {
        int k, x;
        char op;
        cin >> op;
        if(op == 'H')
        {
            cin >> x;
            add_to_head(x);
        }
        else if(op == 'D')
        {
            cin >> k;
            if(!k) head = ne[head];
            remove(k - 1);
        }
        else
        {
            cin >> k >> x;
            add(k - 1, x);
        }
    }
    for(int i = head; i != -1; i = ne[i]) cout << e[i] << " ";

    cout << endl;

    return 0;
}

AcWing 827. 双链表

初始化

void init()
{
    r[0] = 1;   //head -> next = tail
    l[1] = 0;   //tail -> pre = head
    idx = 2;
}

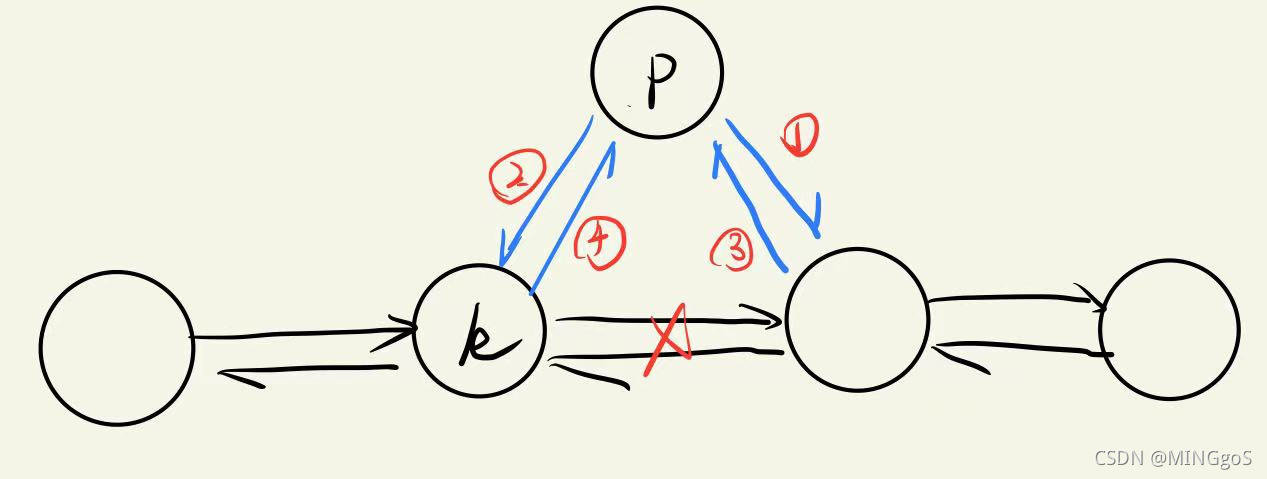
假设p为新节点
插入节点

void add(int k, int x)
{
    e[idx] = x;
    r[idx] = r[k];  // p -> next = k -> next
    l[idx] = k;     // p -> pre = k
    l[r[k]] = idx;  // p -> next -> pre = p
    r[k] = idx;     // k -> next = p
    idx ++;
}

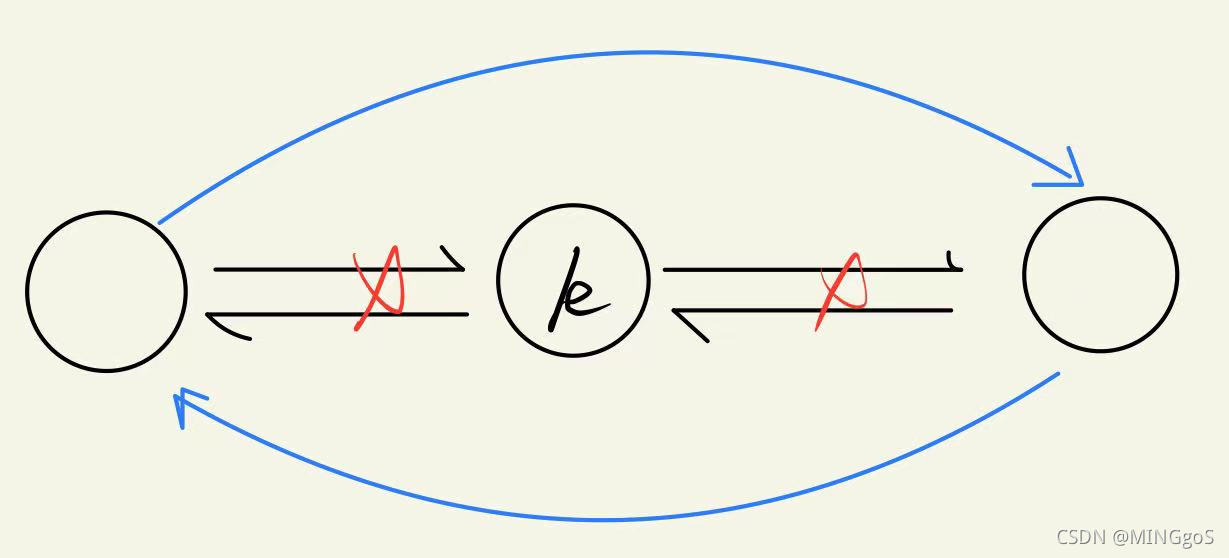
删除节点

void remove(int k)
{
    r[l[k]] = r[k]; // k -> pre -> next = k -> next;
    l[r[k]] = l[k]; // k -> next -> pre = k -> pre;
}

#include<iostream>
using namespace std;

const int N = 1e5 + 10;

int m;
int e[N], r[N], l[N], idx;

void init()
{
    r[0] = 1, l[1] = 0;
    idx = 2;
}

void add(int k, int x)
{
    e[idx] = x;
    r[idx] = r[k];
    l[idx] = k;
    l[r[k]] = idx;
    r[k] = idx;
    idx ++;
}

void remove(int k)
{
    r[l[k]] = r[k];
    l[r[k]] = l[k];
}

int main()
{
    cin >> m;

    init();

    while(m--)
    {
        string op;
        cin >> op;
        int k, x;
        if(op == "L")
        {
            cin >> x;
            add(0, x);
        }
        else if(op == "R")
        {
            cin >> x;
            add(l[1], x);
        }
        else if(op == "D")
        {
            cin >> k;
            remove(k + 1);
        }
        else if(op == "IL")
        {
            cin >> k >> x;
            add(l[k + 1], x);
        }
        else
        {
            cin >> k >> x;
            add(k + 1, x);
        }
    }

    for(int i=r[0]; i!=1; i=r[i]) cout << e[i] << " ";
    cout << endl;

    return 0;
}   

AcWing 828. 模拟栈

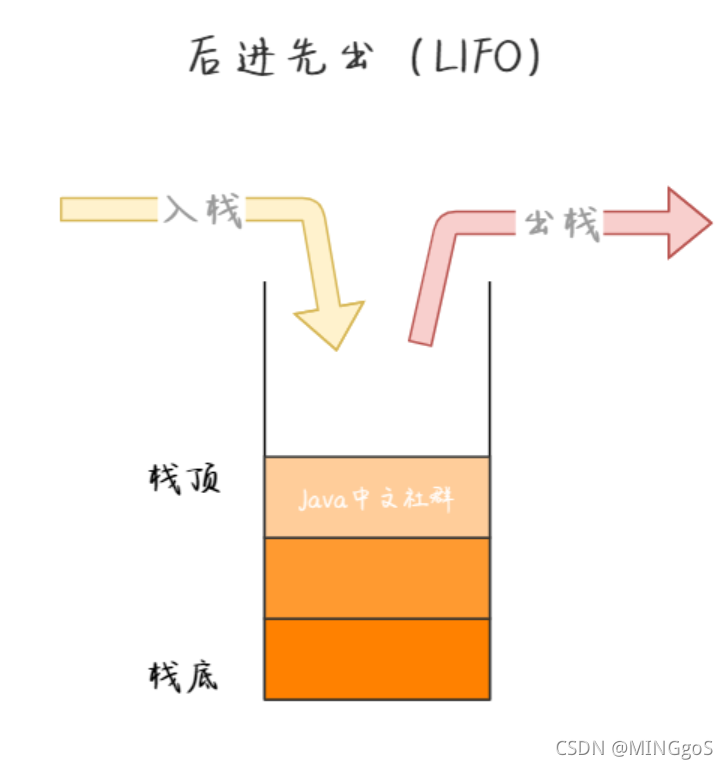
数组模拟栈
tt表示top指针，记录栈顶元素于数组中的位置
tt == 0时，栈为空

#include <iostream>

using namespace std;

const int N = 100010;

int m;
int stk[N], tt;

int main()
{
    cin >> m;
    while (m -- )
    {
        string op;
        int x;

        cin >> op;
        if (op == "push")
        {
            cin >> x;
            stk[ ++ tt] = x;
        }
        else if (op == "pop") tt -- ;
        else if (op == "empty") cout << (tt ? "NO" : "YES") << endl;
        else cout << stk[tt] << endl;
    }

    return 0;
}

AcWing 3302. 表达式求值

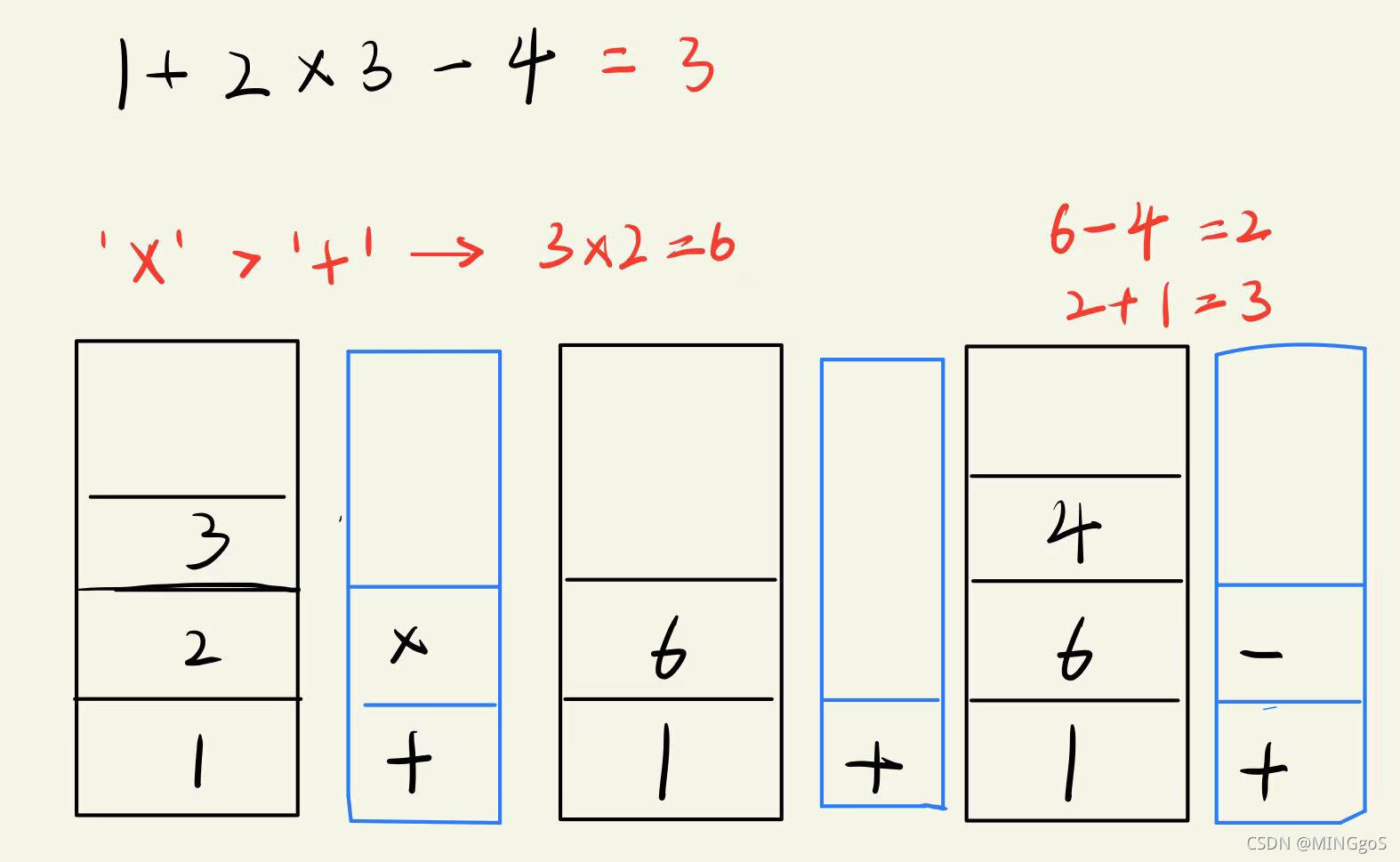
“表达式求值”问题，两个核心关键点：

（1）双栈，一个操作数栈，一个运算符栈；

（2）运算符优先级，栈顶运算符和即将入栈的运算符的优先级比较：
如果栈顶的运算符优先级低，新运算符直接入栈，定义一个哈希表记录各个符号对用的优先级，小括号的优先级最高。
pr{{'+', 1}, {'-', 1}, {'*', 2}, {'/', 2}}
如果栈顶的运算符优先级高，先出栈计算，新运算符再入栈

这个方法的时间复杂度为O(n)，整个字符串只需要扫描一遍。

#include <iostream>
#include <cstring>
#include <algorithm>
#include <unordered_map>
#include <stack>

using namespace std;

void eval(stack<int>& num, stack<char>& op)
{
    int b = num.top(); num.pop();
    int a = num.top(); num.pop();
    char c = op.top(); op.pop();
    int x;
    if (c == '+') x = a + b;
    else if (c == '-') x = a - b;
    else if (c == '*') x = a * b;
    else x = a / b;
    num.push(x);
}

int main()
{
    unordered_map<char, int> pr{{'+', 1}, {'-', 1}, {'*', 2}, {'/', 2}};
    stack<int> num;
    stack<char> op;
    string str;
    cin >> str;

    for (int i = 0; i < str.size(); i ++ )
    {
        char c = str[i];
        if (isdigit(c))
        {
            int j = i, x = 0;
            while (j < str.size() && isdigit(str[j]))
                x = x * 10 + str[j ++ ] - '0';
            num.push(x);
            i = j - 1;
        }
        else if (c == '(') op.push(c);
        else if (c == ')')
        {
            while (op.top() != '(') eval(num, op);
            op.pop();
        }
        else
        {
            while (op.size() && pr[op.top()] >= pr[c]) eval(num, op);
            op.push(c);
        }
    }
    while (op.size()) eval(num, op);
    cout << num.top() << endl;

    return 0;
}

AcWing 829. 模拟队列

hh为队头指针，记录队首在数组中的位置
tt为队尾指针，记录队尾在数组中的位置
hh > tt时，队列为空

#include <iostream>

using namespace std;

const int N = 100010;

int m;
int q[N], hh, tt = -1;

int main()
{
    cin >> m;

    while (m -- )
    {
        string op;
        int x;

        cin >> op;
        if (op == "push")
        {
            cin >> x;
            q[ ++ tt] = x;
        }
        else if (op == "pop") hh ++ ;
        else if (op == "empty") cout << (hh <= tt ? "NO" : "YES") << endl;
        else cout << q[hh] << endl;
    }

    return 0;
}

AcWing 830. 单调栈

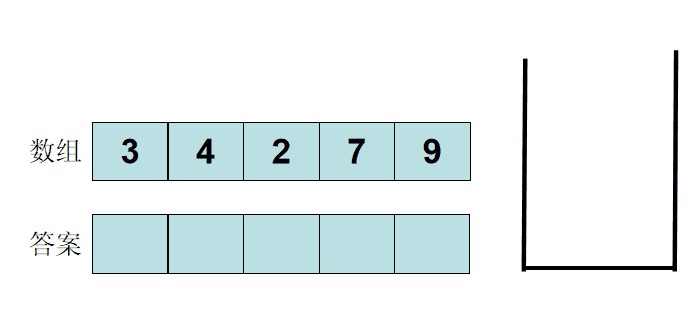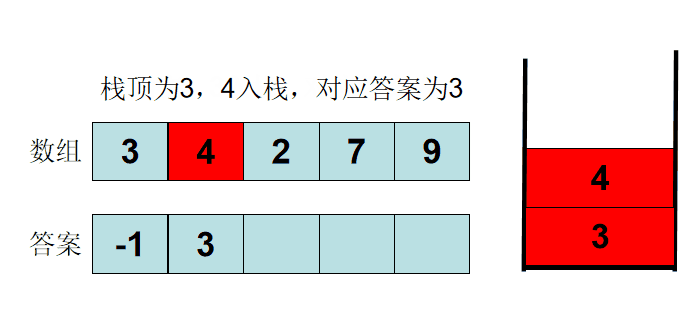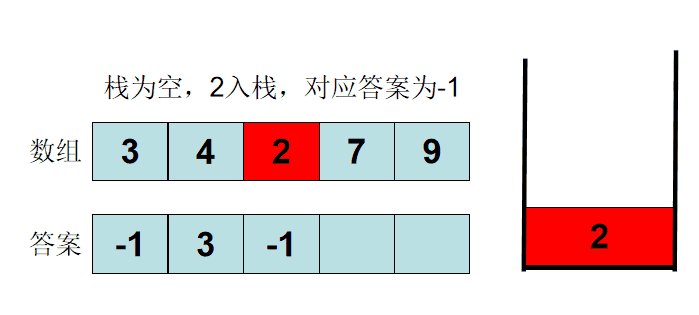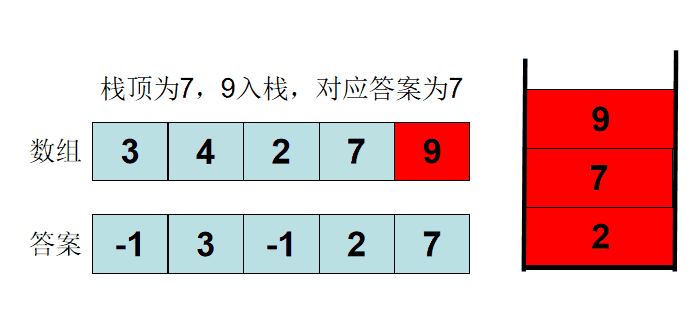
数组模拟

#include<iostream>
using namespace std;

const int N = 1e5 + 10;

int n;
int stk[N], tt;

int main()
{
    scanf("%d", &n);

    for(int i = 0; i < n; i ++ )
    {
        int x;
        scanf("%d", &x);
        while(tt && stk[tt] >= x) tt -- ;
        //栈不为空且栈顶元素大于等于x，则弹出栈顶元素
        if(tt) printf("%d ", stk[tt]);
        //若栈不为空，则输出栈顶元素
        else printf("-1 ");//否则输出-1
        stk[ ++ tt] = x;//x入栈
    }
    return 0;
}

STL

#include<iostream>
#include<stack>
using namespace std;

int main(){
    int x, n;
    scanf("%d", &n);
    stack<int> st;
    for(int i = 0; i < n; i ++ )
    {
        scanf("%d", &x);
        while(!st.empty() && st.top() >= x) st.pop();
        if(!st.empty()) printf("%d ", st.top());
        else printf("-1 ");
        st.push(x);
    }
    return 0;
}

AcWing 154. 滑动窗口

单调队列，类似于单调栈的思想方法
q[i]：记录数组a[i]的元素下标

1. 解决队首已经出窗口的问题，队首下标应在当前窗口覆盖的范围内
2. 解决队尾与当前元素a[i]不满足单调性的问题，不满足单调性的，就直接弹出队尾，直到满足单调性为止
3. 将当前元素下标加入队尾;
4. 如果满足条件则输出队首元素;

以下是一个例子：
该数组为[1 3 -1 -3 5 3 6 7]，k为3。
窗口位置 最小值 最大值
[1 3 -1] -3 5 3 6 7 -1 3
1 [3 -1 -3] 5 3 6 7 -3 3
1 3 [-1 -3 5] 3 6 7 -3 5
1 3 -1 [-3 5 3] 6 7 -3 5
1 3 -1 -3 [5 3 6] 7 3 6
1 3 -1 -3 5 [3 6 7] 3 7
如图，其中q数组记录数值，p数组记录下标

#include<iostream>
using namespace std;

const int N = 1e6 + 10;

int n, k;
int a[N], q[N];

int main()
{
    scanf("%d%d", &n, &k);
    for(int i = 0; i < n; i ++ ) scanf("%d", &a[i]);
    int hh = 0, tt = -1;

    for(int i = 0; i < n; i ++ )
    {
        if(hh <= tt && i - k + 1 > q[hh]) hh ++ ;
        while(hh <= tt && a[q[tt]] >= a[i]) tt -- ;

        q[ ++ tt] = i;
        if(i >= k - 1) printf("%d ", a[q[hh]]);
    }
    puts("");

    hh = 0, tt = -1;
    for(int i = 0; i < n; i ++ )
    {
        if(hh <= tt && i - k + 1 > q[hh]) hh ++ ;
        while(hh <= tt && a[q[tt]] <= a[i]) tt -- ;

        q[ ++ tt] = i;
        if(i >= k - 1) printf("%d ", a[q[hh]]);
    }
    puts("");

    return 0;
}

AcWing 831. KMP字符串

一、暴利匹配的模式
第一个过程：子串“goo”部分与主串相等，’g’不等，结束比对，进行回溯。

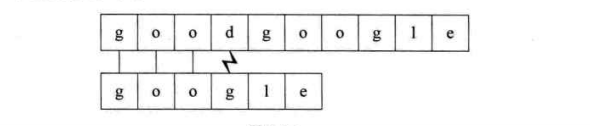
第二个过程：开始时就不匹配，直接回溯

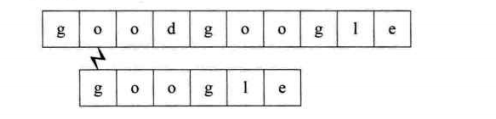
第三个过程：开始时即不匹配，直接回溯

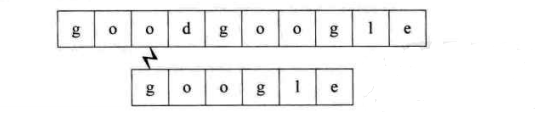
第四个过程：开始时即不匹配，直接回溯

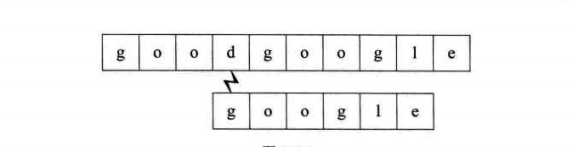
第五个过程：匹配成功

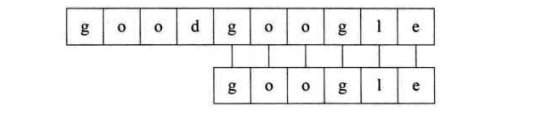
模式串长度为m，匹配串长度为n，时间复杂度为$O(n*m)$
二、KMP算法
前置概念
公式：

动图演示：

求出模式串的next数组之后进行字符串匹配
以目标串：s，指针为 i ；模式串：t 指针为 j ; 为例

上图表示：“si-j ~ si-1” == “t 0 ~ t j-1”，si != tj（前面都相等，但比较到 t j 时发现不相等了）且next[j] == k。

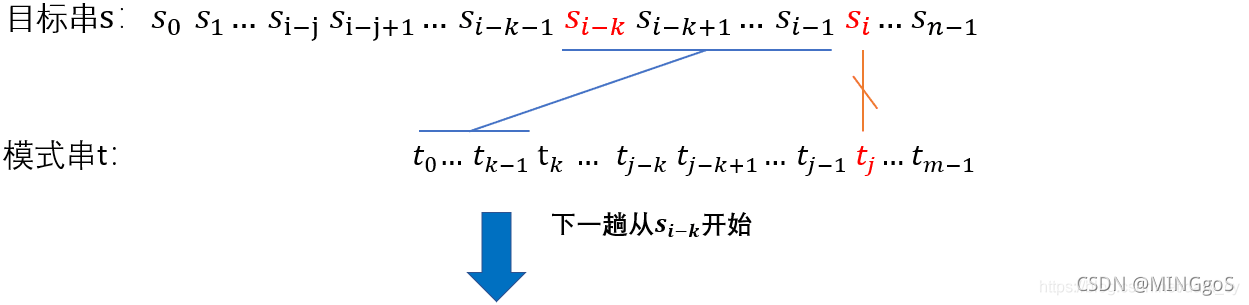
根据 next 数组的定义得知“t k ~ t j-1” == “t 0 ~ t k-1”，所以 “t 0 ~ t k-1” == “si-k ~ si-1”

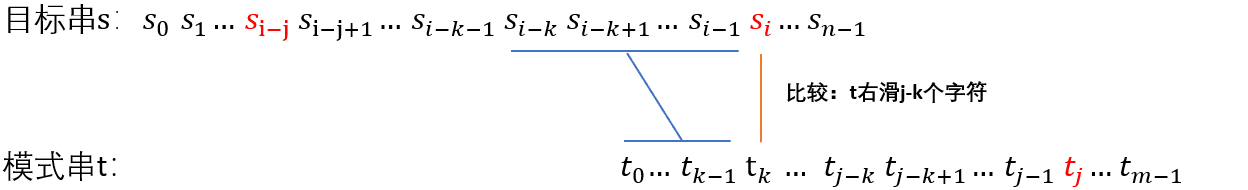
将模式串右移，得到上图，这样就避免了目标穿的指针回溯。
思想方法和分形相似

#include<iostream>
using namespace std;

const int N = 1e5 + 10, M = 1e6 + 10;

int n, m;
char p[N], s[M];
int ne[N];

int main()
{
    cin >> n >> p + 1 >> m >> s + 1;
    for(int i = 2, j = 0; i <= n; i ++ )
    {
        while(j && p[i] != p[j + 1]) j = ne[j];
        if(p[i] == p[j + 1]) j ++ ;
        ne[i] = j;
    }

    for(int i = 1, j = 0; i <= m; i ++ )
    {
        while(j && s[i] != p[j + 1]) j = ne[j];
        if(s[i] == p[j + 1]) j ++ ;
        if(j == n)
        {
            cout << i - n << " ";
            j = ne[j];
        }
    }
    return 0;
}

AcWing 835. Trie字符串统计

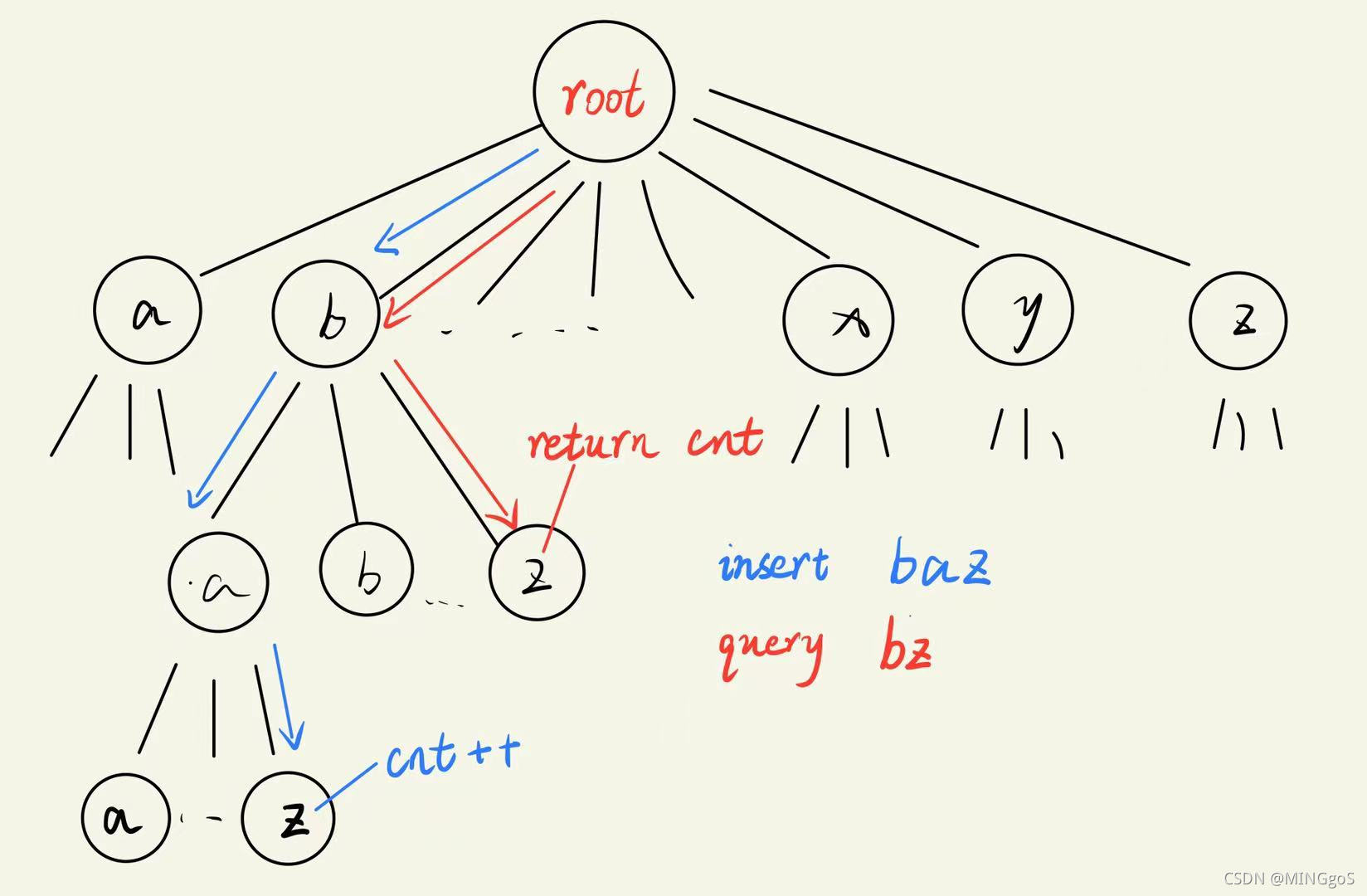
son[i][26]:存放子节点的指针
例如son[1][0] = 2表示存放节点1的子节点a的指针为2
cnt[i]：利用每个字符串最后一个字符的位置可以记录每个字符串出现的次数
插入函数：

void insert(char str[])
{
    int p = 0;                  //从根结点开始遍历
    for(int i = 0; str[i]; i ++ )
    {
        int u = str[i] - 'a';

        if(!son[p][u])
            son[p][u] = ++ idx; //说明该节点没有走过，给它编号 
        p = son[p][u];          //走到p的子结点u
    }

        cnt[p] ++ ;             //标记该节点为字符串的末尾，或者记录信息
}

查询函数

int query(char str[])
{
    int p = 0;
    for(int i = 0; str[i]; i ++ )
    {
        int u = str[i] - 'a';
        if(!son[p][u]) return 0;//该字符没有插入过
        p = son[p][u];          //相当于 p = p -> next 的操作
    }

    return cnt[p];
}

#include<iostream>
using namespace std;

const int N = 1e5 + 10;

int son[N][26], cnt[N]; //每个节点编号都可能作为一个字符串的末尾
int idx;                //全局变量，记录所有节点的数量
char str[N];

void insert(char str[])
{
    int p = 0;//从根结点开始遍历
    for(int i = 0; str[i]; i ++ )
    {
        int u = str[i] - 'a';

        if(!son[p][u])
            son[p][u] = ++ idx; //说明该节点没有走过，给它编号 
        p = son[p][u]; //走到p的子结点
    }

    cnt[p] ++ ;//标记该节点为字符串的末尾，或者记录信息
}

int query(char str[])
{
    int p = 0;
    for(int i = 0; str[i]; i ++ )
    {
        int u = str[i] - 'a';
        if(!son[p][u]) return 0;//该字符没有插入过
        p = son[p][u];
    }

    return cnt[p];
}

int main()
{
    int n;
    scanf("%d", &n);
    while(n -- )
    {
        char op[2];
        scanf("%s%s", op, str);
        if(op[0] == 'I') insert(str);
        else printf("%d\n", query(str));
    }

    return 0;
}

AcWing 143. 最大异或对

以二进制数的形式将每个数字存进字典树
然后查询的时候优先寻找是否存在高位数字的异或，没有异或位再去找相同位

#include<iostream>
#include<algorithm>

using namespace std;

const int N = 1e5 + 10, M = 31 * N;

int n;
int a[N];
int son[M][2], idx;

void insert(int x)
{
    int p = 0;
    for(int i = 30; i >= 0; i -- )
    {
        int u  = x >> i & 1;
        if(!son[p][u]) son[p][u] = ++ idx;
        p = son[p][u];
    }
}

int query(int x)
{
    int p = 0, res = 0;
    for(int i = 30; i >= 0; i -- )  //从高位数字开始
    {
        int u = x >> i & 1;
        if(son[p][!u])              //优先异或位
        {
            p = son[p][!u];
            res = res * 2 + !u;
        }
        else
        {
            p = son[p][u];
            res = res * 2 + u;
        }
    }
    return res;
}

int main()
{
    scanf("%d", &n);
    for(int i = 0; i < n; i ++ ) scanf("%d", &a[i]);

    int res = 0;

    for(int i = 0; i < n; i ++ )
    {
        insert(a[i]);
        int t = query(a[i]);
        res = max(res, a[i] ^ t);
    }

    printf("%d\n", res);

    return 0;
}

AcWing 836. 合并集合

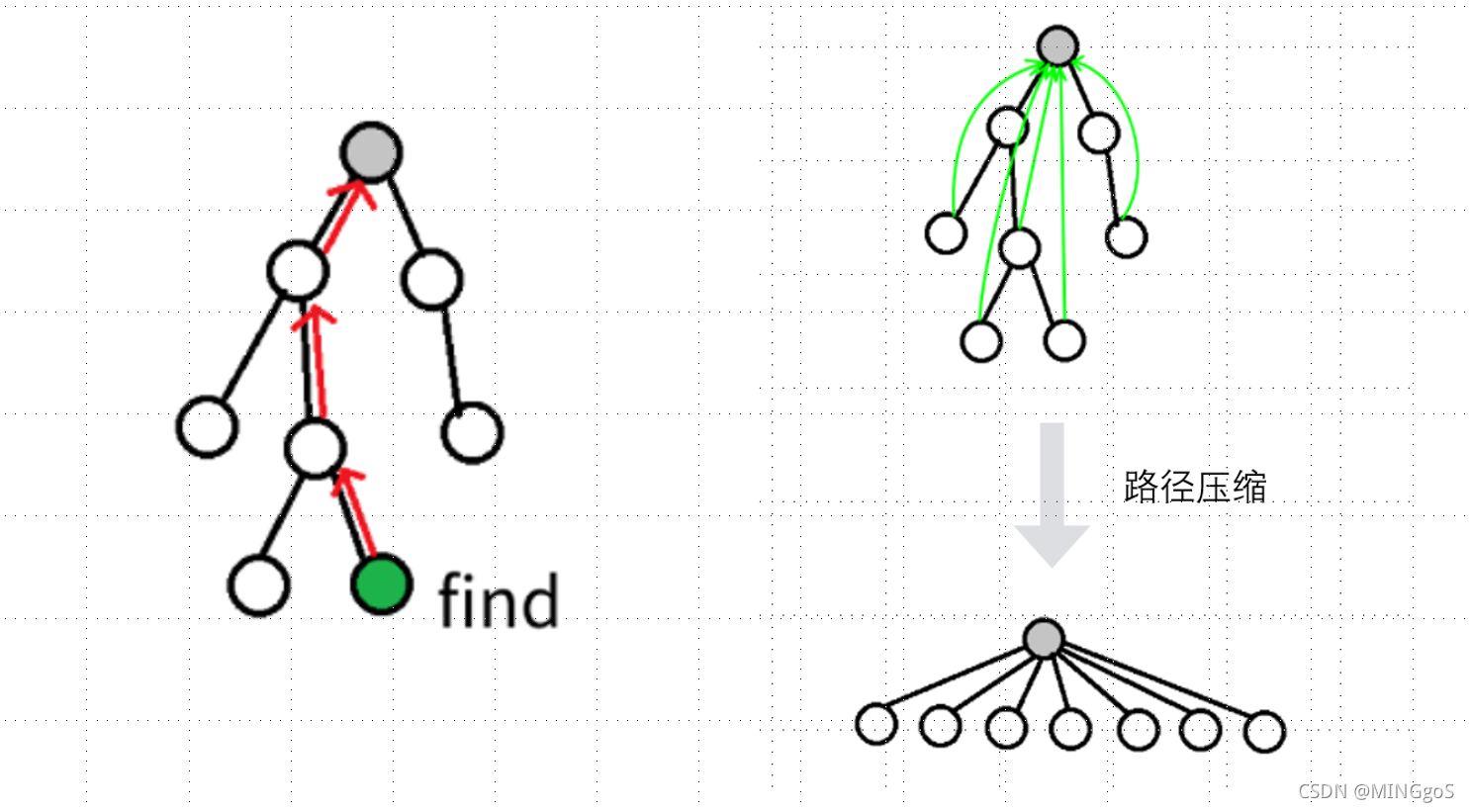
并查集是一个树形的结构，每个集合都有一个祖宗节点，每次查找集合成员都会递归的返回该节点对应的父亲节点

int find(int x)
{
    if(x != fa[x]) return find(fa[x]);
    return x;
}

路径压缩:将每次查询的节点的父亲节点直接改为祖宗节点

int find(int x)
{
    if(p[x] != x) p[x] = find(p[x]);
    return p[x];
}

#include<iostream>
using namespace std;

const int N = 1e5 + 10;

int n, m;
int p[N];

int find(int x)
{
    if(p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i ++ ) p[i] = i;
    while(m -- )
    {
        char op[2];
        int a, b;
        cin >> op >> a >> b;

        if(op[0] == 'M') p[find(a)] = find(b);
        else
        {
            if(find(a) == find(b)) puts("Yes");
            else puts("No");
        }
    }
    return 0;
}

AcWing 837. 连通块中点的数量

利用并查集的特性维护一个记录每个集合有多少个点的数组，cnt数组中祖宗节点对应的下标记录每个集合的点的数量。

#include<iostream>
using namespace std;

const int N = 1e5 + 10;

int n, m;
int p[N], Size[N];

int find(int x)
{
    if(p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i ++ )
    {
        p[i] = i;
        Size[i] = 1;
    }
    while(m -- )
    {
        char op[5];
        int a, b;
        cin >> op;

        if(op[0] == 'C')
        {
            cin >> a >> b;
            if(find(a) == find(b)) continue;

            Size[find(b)] += Size[find(a)];
            p[find(a)] = find(b);
        }
        else if(op[1] == '1')
        {
            cin >> a >> b;
            if(find(a) == find(b)) puts("Yes");
            else puts("No");
        }
        else
        {
            cin >> a;
            cout << Size[find(a)] << endl;
        }
    }
}

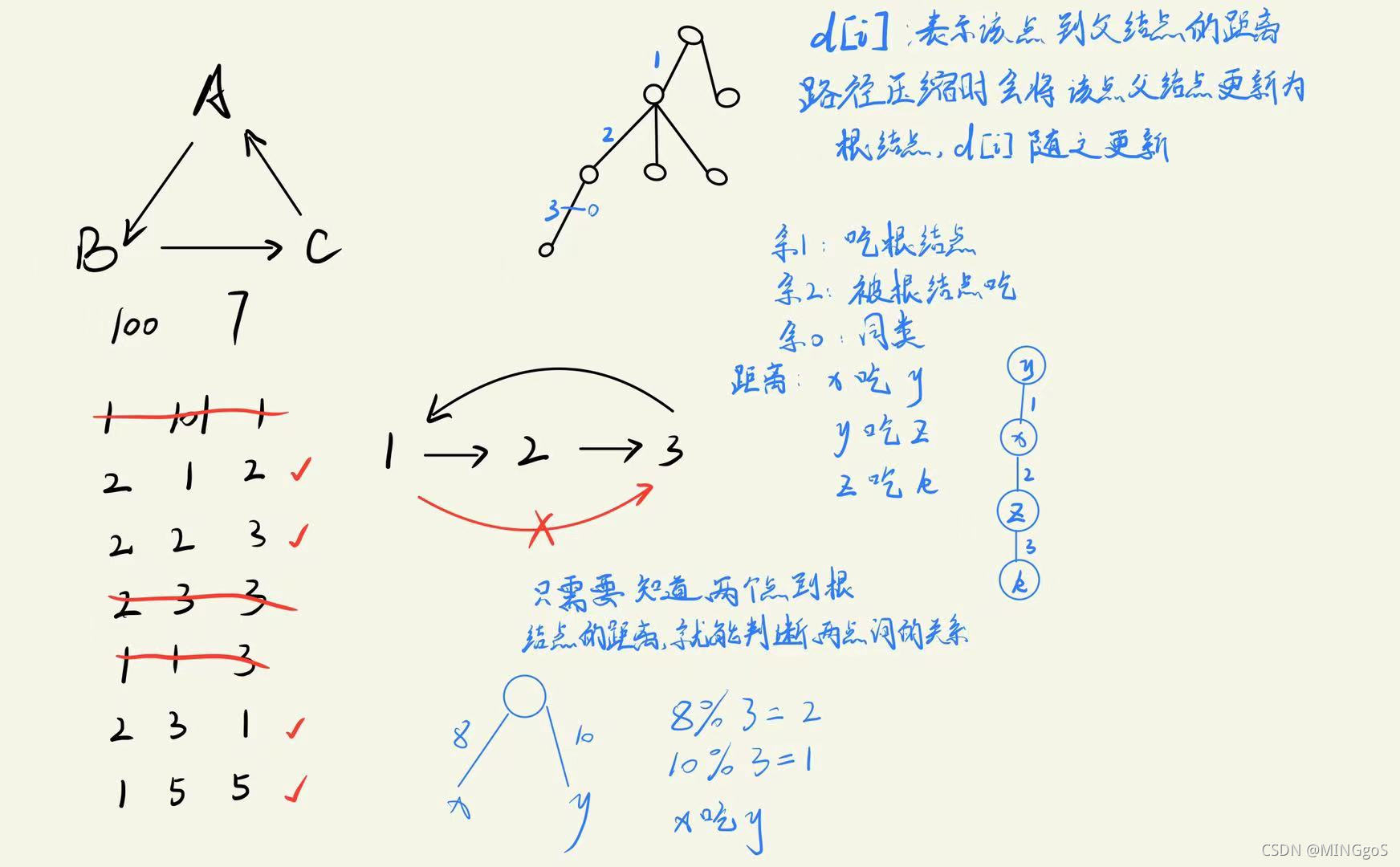
AcWing 240. 食物链

#include <iostream>

using namespace std;

const int N = 50010;

int n, m;
int p[N], d[N];

int find(int x)
{
    if (p[x] != x)
    {
        int t = find(p[x]);

        //路径压缩，将该点的父节点更新为祖宗节点，并将距离更新
        d[x] += d[p[x]];
        p[x] = t;
    }
    return p[x];
}

int main()
{
    scanf("%d%d", &n, &m);

    for (int i = 1; i <= n; i ++ ) p[i] = i;

    int res = 0;
    while (m -- )
    {
        int t, x, y;
        scanf("%d%d%d", &t, &x, &y);

        if (x > n || y > n) res ++ ;
        else
        {
            int px = find(x), py = find(y);

            //t = 1，x和y应该为同类
            if (t == 1)
            {
                //当x和y到根节点的距离之差不为0时为假话
                if (px == py && (d[x] - d[y]) % 3)
                    res ++ ;

                //合并两个集合
                else if (px != py)
                {
                    p[px] = py;
                    d[px] = d[y] - d[x];
                }
            }

            //t = 2，x和y之间应该为吃与被吃的关系
            else
            {
                //如果是吃与被吃的关系，那么两点到根节点的距离之差的绝对值应该为1
                if (px == py && (d[x] - d[y] - 1) % 3)
                    res ++ ;

                //合并集合
                else if (px != py)
                {
                    p[px] = py;
                    d[px] = d[y] + 1 - d[x];
                }
            }
        }
    }

    printf("%d\n", res);

    return 0;
}

AcWing 838. 堆排序

1. 为什要从i = n / 2开始down？

2. 首先要明确要进行down操作时必须满足左儿子和右儿子已经满足堆的性质，即左右子树都是堆。

3. 开始创建堆的时候，元素是随机插入的，所以不能从根节点开始down，而是要找到满足下面三个性质的结点：
4. 左右儿子满足堆的性质。
5. 下标最大（因为要往上遍历）
6. 不是叶结点（叶节点一定满足堆的性质）

#include<iostream>
#include<algorithm>
using namespace std;

const int N = 1e5 + 10;

int n, m;
int h[N], cnt;

void down(int u)
{
    int t = u;  //t标记最小值

    if(u * 2 <= cnt && h[u * 2] < h[t]) t = u * 2;
    if(u * 2 + 1 <= cnt && h[2 * u + 1] < h[t]) t = u * 2 + 1;

    if(u != t)  //根结点不是最小值
    {
        swap(h[u], h[t]);
        down(t);
    }
}

int main()
{
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i ++ ) scanf("%d", &h[i]);
    cnt = n;

    for(int i = n / 2; i; i -- ) down(i);

    while(m -- )
    {
        printf("%d ", h[1]);
        h[1] = h[cnt];
        cnt -- ;
        down(1);
    }
    return 0;
}

AcWing 839. 模拟堆

hp是heap pointer的缩写，表示堆数组中下标到第k个插入的映射
ph是pointer heap的缩写，表示第k个插入到堆数组中的下标的映射
hp和ph数组是互为反函数的

#include <iostream>
#include <algorithm>
#include <string.h>

using namespace std;

const int N = 100010;

int h[N], ph[N], hp[N], cnt;

void heap_swap(int a, int b)
{
    swap(ph[hp[a]],ph[hp[b]]);
    swap(hp[a], hp[b]);
    swap(h[a], h[b]);
}

void down(int u)
{
    int t = u;
    if (u * 2 <= cnt && h[u * 2] < h[t]) t = u * 2;
    if (u * 2 + 1 <= cnt && h[u * 2 + 1] < h[t]) t = u * 2 + 1;
    if (u != t)
    {
        heap_swap(u, t);
        down(t);
    }
}

void up(int u)
{
    while (u / 2 && h[u] < h[u / 2])
    {
        heap_swap(u, u / 2);
        u >>= 1;
    }
}

int main()
{
    int n, m = 0;
    scanf("%d", &n);
    while (n -- )
    {
        char op[5];
        int k, x;
        scanf("%s", op);
        if (!strcmp(op, "I"))
        {
            scanf("%d", &x);
            cnt ++ ;
            m ++ ;              //记录第几次插入
            ph[m] = cnt, hp[cnt] = m;
                                //每次插入都是在堆尾插入
            h[cnt] = x;         //记录插入的值
            up(cnt);
        }
        else if (!strcmp(op, "PM")) printf("%d\n", h[1]);
        else if (!strcmp(op, "DM"))
        {
            heap_swap(1, cnt);
            cnt -- ;
            down(1);
        }
        else if (!strcmp(op, "D"))
        {
            scanf("%d", &k);
            k = ph[k];
                                //必须要保存当前被删除结点的位置
            heap_swap(k, cnt);  //第k个插入的元素移到了堆尾，此时ph[k]指向堆尾 
            cnt -- ;            //删除堆尾
            up(k);              //k是之前记录被删除的结点的位置
            down(k);
        }
        else
        {
            scanf("%d%d", &k, &x);
            k = ph[k];
            h[k] = x;
            up(k);
            down(k);
        }
    }

    return 0;
}

AcWing 840. 模拟散列表

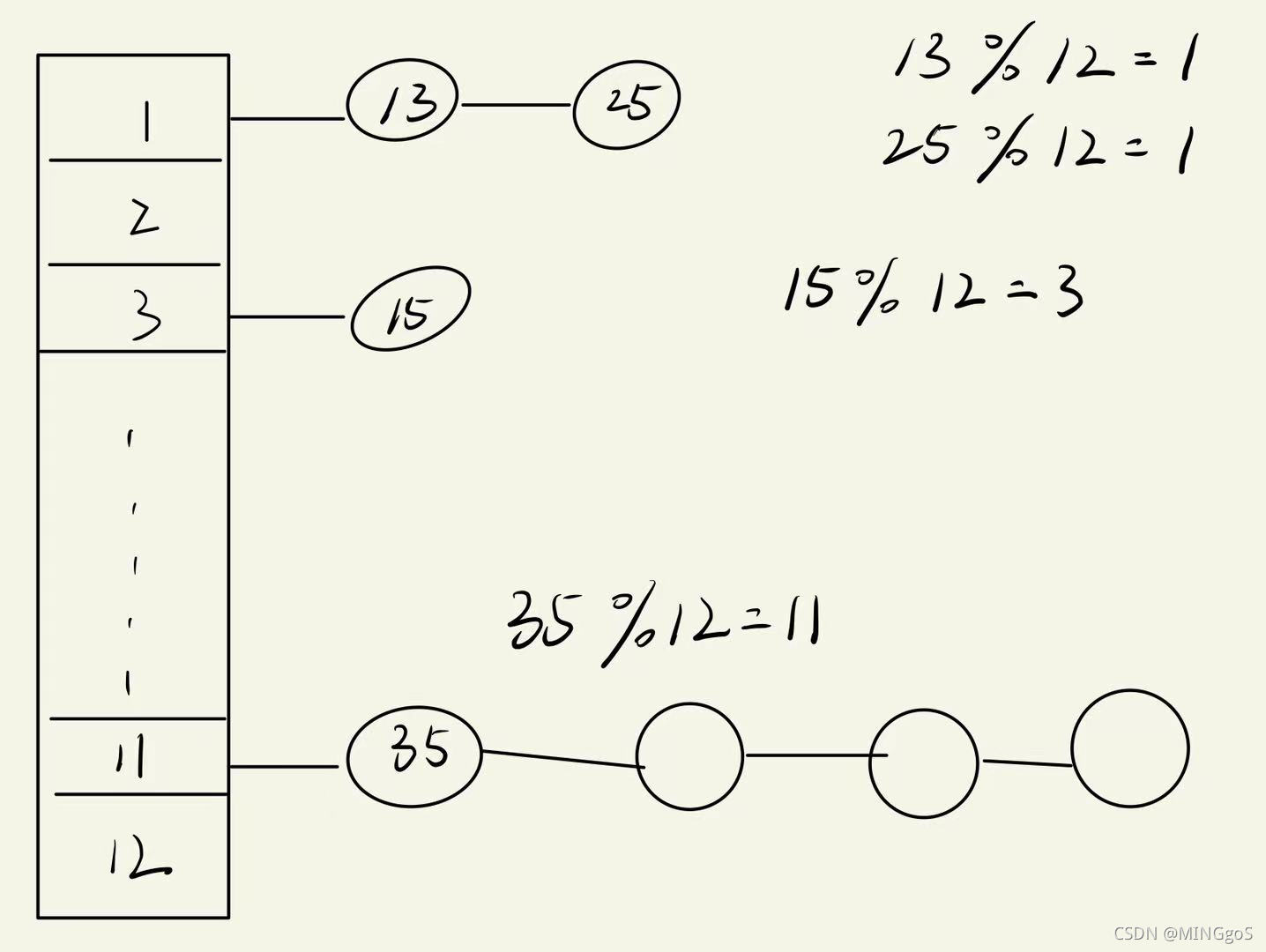
1.拉链法
用一个数组存放头结点，然后将用单链表将对应的数值取模后存进对应的链表中

#include<iostream>
#include<cstring>
using namespace std;

const int N = 1e5 + 3;
int h[N], e[N], ne[N], idx;

void insert(int x)
{
    int k = (x % N + N) % N;
    e[idx] = x;
    ne[idx] = h[k];
    h[k] = idx++;
}

bool find(int x)
{
    int k = (x % N + N) % N;
    for(int i = h[k]; i != -1; i = ne[i])
        if(e[i] == x)
            return true;

    return false;
}

int main()
{
    int n;
    scanf("%d", &n);

    memset(h, -1, sizeof h);

    while(n--)
    {
        char op[2];
        int x;
        scanf("%s%d", op, &x);

        if(*op == 'I') insert(x);
        else
        {
            if(find(x)) puts("Yes");
            else puts("No");
        }
    }
    return 0;
}

2.开放寻址法
哈希运算后的位置pos有冲突的话，pos ++直到不冲突为止

#include <cstring>
#include <iostream>

using namespace std;

const int N = 200003, null = 0x3f3f3f3f;

int h[N];

int find(int x)
{
    int t = (x % N + N) % N;
    while (h[t] != null && h[t] != x)
    {
        t ++ ;
        if (t == N) t = 0;
    }
    return t;
}

int main()
{
    memset(h, 0x3f, sizeof h);

    int n;
    scanf("%d", &n);

    while (n -- )
    {
        char op[2];
        int x;
        scanf("%s%d", op, &x);
        if (*op == 'I') h[find(x)] = x;
        else
        {
            if (h[find(x)] == null) puts("No");
            else puts("Yes");
        }
    }

    return 0;
}

AcWing 841. 字符串哈希

时间复杂度 $O(n)+O(m)$

全称字符串前缀哈希法，把字符串变成一个p进制数字（哈希值），实现不同的字符串映射到不同的数字。

对形如 $X1X2X3⋯Xn−1Xn$ 的字符串,采用字符的ascii 码乘上 P 的次方来计算哈希值。

映射公式 $(X1×Pn−1+X2×Pn−2+⋯+Xn−1×P1+Xn×P0)modQ$

前缀和公式 $h[i+1]=h[i]×P+s[i], i∈[0,n−1]$，h为前缀和数组，s为字符串数组

区间和公式 $h[l,r]=h[r]−h[l−1]×Pr−l+1$

区间和公式的理解:ABCDE 与 ABC 的前三个字符值是一样，只差两位，
乘上P2把 ABC 变为 ABC00，再用ABCDE - ABC00得到 DE 的哈希值

#include<iostream>
using namespace std;

typedef unsigned long long ULL;
const int N = 1e5 + 10, P = 131;

int n, m;
char str[N];
ULL h[N], p[N];

ULL get(int l, int r)
{
    return h[r] - h[l - 1] * p[r - l + 1];
}

int main()
{
    scanf("%d%d%s", &n, &m, str + 1);

    p[0] = 1;
    for(int i = 1; i <= n; i ++)
    {
        p[i] = p[i - 1] * P;
        h[i] = h[i - 1] * P + str[i];
    }

    while(m -- )
    {
        int l1, r1, l2, r2;
        scanf("%d%d%d%d", &l1, &r1, &l2, &r2);

        if(get(l1, r1) == get(l2, r2)) puts("Yes");
        else puts("No");
    }

    return 0;
}