第二章 随机变量及其分布
本章将介绍非常有用的概念—随机变量, 随机变量可以简化概率表达, 加强人们量化不确定现象和总结实验
结果的能力. 随机变量将贯穿本书以及整个统计学领域, 因此无论从直观上还是数学上都需要深入理解什么
是随机变量.
3.1 随机变量
为认识到我们之前对不确定现象的表达是多么的不明智, 再次回到第二章例 2.7.3 赌徒输光问题. 在这个
问题中, 人们对赌徒在任意时刻还剩多少财产感兴趣, 因此补充表达式: 假设事件$A_{jk}$表示赌徒A在$k$
轮赌博后恰好剩下$j$美元, 类似的, 定义$B_{jk}$.
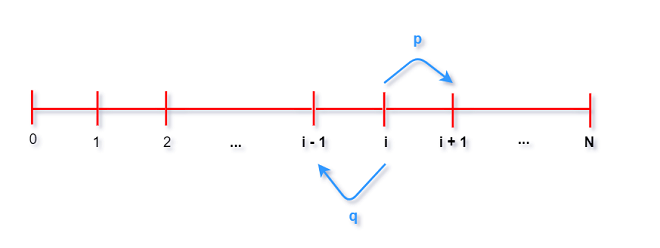
显然, 上述表达过于复杂. 此外人们也会对其他问题感兴趣, 例如在$k$轮赌博之后两个赌徒所剩财产的差额是
多少, 或者赌博的持续时间. 对于“这局赌博的持续时间”问题, 如果用$A_{jk}$和$B_{jk}$来表示的话, 会变得非常冗杂. 此外如果我们想用等价值的欧元来表示赌徒A的财产又该如何表示? 美元和欧元的转换可以根据汇率乘以数字计算, 然而事件却没有类似的转换比例可以相乘.
如果用下面的描述方式代替上述复杂符号, 可能会得到更好的效果.
设$X_k$表示赌徒A在$k$轮赌博之后的财产($X$变量<-->$j$常量). 那么$Y_k = N - X_k$可以表示赌徒B剩余
的财产($N$是两个赌徒财产总和), $Y_k - X_k = N - 2X_k$表示在$k$轮赌博之后两个赌徒所剩财产的差额, $c_kX_k$
指用等价值欧元来表示赌徒A的财产, $c_k$是欧元对美元的汇率, 此外$R = min${$n : X_n=0或Y_n=0$}可以
表示游戏的持续时间.
随机变量就能描述以上问题. 在掌握随机变量时需要仔细介绍其定义, 保证概念上和技术上的正确性. 随机变量
有时被定义为: 带有随机性质的变量, 然而这并不能解释出随机性从哪里来, 也不能得到随机变量的性质, 例如对
代数方程$x^2 + y^2 = 1$, 如果$x, y$均是随机变量, 那么应该如何进行数学运算(根据定义$x,y$是随机的).
为满足准确定义, 我们将随机变量定义为样本空间到实数轴上的函数映射.
3.1.1 随机变量
给定样本空间$S$上的一个试验, 随机变量(random variable, 记作r.v.)是从样本空间$S$到实数轴R上的函数,
通常用大写字母表示.
因此, 一个随机变量$X$为试验的每个可能结果$s$分配数值$X(s)$. 而随机性来源有一个随机试验(有概率函数$P$描述).
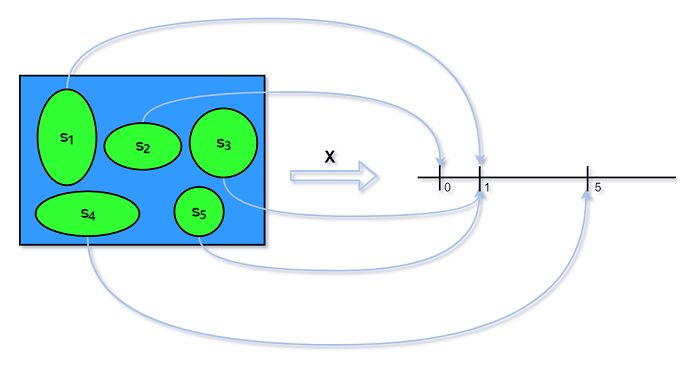
如上图所示, 样本空间的5个元素通过随机变量$X$映射到实数轴上. $X$的随机性源于根据样本空间的概率函数$P$,
哪个元素的发生是随机的.
考虑一个抛硬币的例子. 问题的结构是: 做一系列试验, 每个试验都有两种可能的结果. 这里认为可能的结果
包括$H$(正面朝上)和$T$(反面朝上), 也可看作$1$和$0$.
例 3.1.2 抛硬币
考虑一个试验: 随机地抛2次硬币. 此时样本空间由4个可能结果组成: $S = \lbrace HH,HT,TH,TT\rbrace $.
这里存在该空间上的一些随机变量, 每个随机变量都是试验在某方面的数值表示.
-
设$X$表示正面朝上的次数. $X$是一个随机变量, 其可能的取值为$0、1、2$. 将其看作一个函数,
有$X(HH) = 2$,$X(TH) = X(HT) = 1$, $X(TT) = 0$. -
设$Y$表示反面朝上的次数. 对于$X$, 有$Y = 2 - X$. 也就是对于$Y$和$2 - X$是相同的
r.v.:
对于任意的试验结果$s$, 有$Y(s) = 2 - X(s)$. -
设$I$是随机变量, 如果第一次硬币正面朝上则$I$取值为$1$, 反之为$0$. 也就是$I(HH) = I(HT) = 1$,
$I(TH) = I(TT) = 0$. 由于该随机变量表示硬币第一次是否正面朝上(用$1$表示“是”, $0$表示“否”)
因此随机变量$I$也叫做 实性随机变量 .
样本空间也可以被重新标注为$S = \lbrace 11,10,01,00\rbrace $, 其中$1$表示正面朝上, $0$表示反面朝上.
此时可以给出$X、Y$和$I$的确切表达式:
$\;\;\;\;X(s_1,s_2) = s_1 + s_2, Y(s_1,s_2) = 2 - s_1 - s_2, I(s_1,s_2) = s1$
其中, 为使符号简便, 将$X((s_1,s_2))$标记为$X(s_1,s_2)$, 以此类推.
对于之后将考虑的大多数随机变量而言, 这样写出一个明确的表达式往往是冗长的甚至是不可行的. 幸运的是,
通常没有必要如此操作, 因为可以通过其他方法定义一个随机变量(正如本例所示), 并且除了通过显式的公式
来计算得到其对每个试验结果的映射外, 还有许多方法研究随机变量的性质(我们会在本书剩余部分看到).
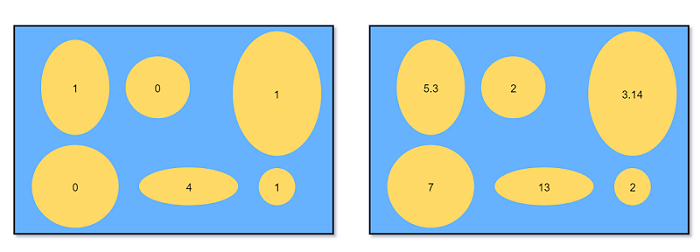
如之前章节提到的, 对于有限样本空间, 可以将每个结果看作一个鹅卵石(pebble's world), 相应的概率可以
表示成卵石的质量, 卵石质量的总和为$1$. 随机变量可以简单的表示为对每个卵石标记数值.
(assign each pebble a number)
下图显示定义在同一个样本空间的两个随机变量: 鹅卵石/结果相同, 但实际分配数值不同.
随机变量的随机性
正如前面所提到的, 随机变量中的随机性来源于试验本身. 在试验中, 样本结果$s\in S$是根据一个概率函数$P$
进行选择的. 在试验开始前, 试验结果是未知的, 因此我们不知道随机变量$X$的取值, 尽管可以计算随机变量$X$
在给定值或取值范围内的概率(概率实际上就表明了随机性). 当执行完试验并观测到结果后, 随机变量就可以具体
化为数值形式$X(s)$.
随机变量提供数值摘要
随机变量提供了有关试验的数值摘要. 这是非常方便的, 因为一个试验的样本空间通常是非常复杂或者是高维的,
且试验结果$s\in S$还有可能是非数值的. 例如, 某试验结果可能是在某个大学学生中随机抽样, 然后向他们
询问各种问题, 问题的结果可能是数字(如身高)或非数字(如喜欢的游戏)形式的. 相比于需要始终处理非常复杂
的样本空间$S$, 以数值形式呈现的随机变量是一种非常方便的简化.
这很类似Y式DP的思路: 考虑用集合描述一个问题, 这个集合可能十分庞大复杂, 但我们只需用数值描述该集合
的某个属性.
3.2 随机变量的分布于概率质量函数
全部可能取到的值为有限个或可列无限多个,这种随机变量称为离散型随机变量.
骰子的点数,打靶环数,某城市120急救电话一昼夜收到的呼叫次数,都是离散型随机变量
如果$X$是一个离散型随机变量, 然后存在关于$x$值的有限或可数无穷集合$\lbrace x \rbrace$, 使得$P(X=x)\gt 0$,
则称这个集合为$X$的支撑(support)或支撑集.
概率语言描述随机变量
给定一个随机变量, 通常人们希望用概率语言来描述它的表现. 例如我们可能知道“随机变量将落在一定范
围内的概率”的问题: 假设随机变量$L$表示随机选择一名用户通过AcWing某次周赛题目的个数, 那么$L$
超过2个概率是多少?
一个随机变量的分布(distribution)可以给出上问题的答案, 它可以给出与之相关的所有时间的概率,
比如$L$大于2的概率. 之后会看到几个等效的方法表示一个离散型随机变量的分布, 最常用的也是最
自然的方法是通过 概率质量函数, 下面给出其定义.
定义 3.2.2 概率质量函数
离散型随机变量$X$的概率质量函数(probability mass function, PMF)是一个形如$p_X(x) = P(X=x)$的
函数, 写作$p_X$. 如果$x$是随机变量$X$的支撑, 那么$p_X\gt 0$, 否则$p_x = 0$.
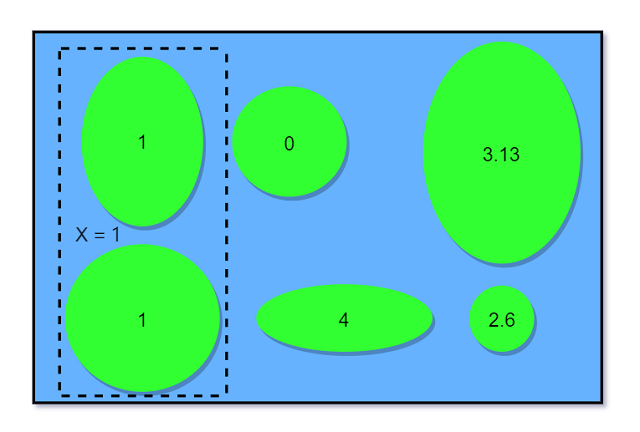
-ω- 3.2.3 $X=x$的含义
在书写$P(X=x)$时, 用$X=x$表示一个事件, 它由$X$分配给$x$的所有结果组成. 事件可以写成$\lbrace X=x\rbrace$,
严格来说$\lbrace X=x\rbrace$应定义成$s\in S, X(s)=x$, 不过$\lbrace X=x\rbrace$更简洁直观. 回到例 3.1.2 抛硬币
, 如果随机变量$X$表示正面朝上的次数, 那么$\lbrace X=1\rbrace$由样本结果$\lbrace HT \rbrace TH$组成, $X$
作用到$\lbrace HT \rbrace TH$的值就是$1$. $\lbrace HT \rbrace TH$是样本空间的一个子集, 所以是一个事件.
因此讨论$P(X=1)$或更一般的$P(X=x)$是有意义的. $P(X)$是无意义的, 随机变量并不是一个事件.
下图表示$X=1$对于事件:
接下来介绍几个关于概率质量函数(PMF)的例子.
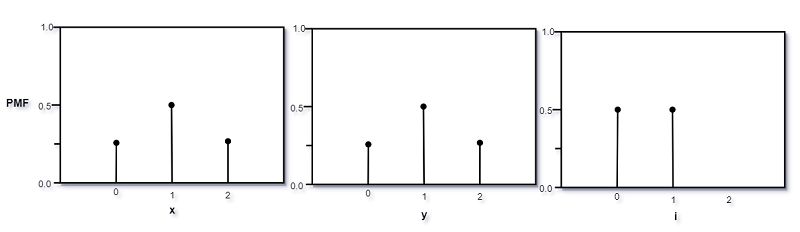
例 3.2.4 抛硬币续
本例将求出例 3.1.2 抛硬币中所有随机变量的概率质量函数, 例 3.1.2已知抛掷两枚均匀硬币. 下面是我们
定义的随机变量还有它们的概率质量函数:
-
$X$表示正面朝上的次数. 问题可以应用朴素概率定义, $X(HH)=2, X(TH)=X(HT)=1, X(TT)=0$, 所以随机变量$X$的
概率质量函数$p_X$定义如下:
$\;\;\;\;\;\;p_X(0) = P(X = 0) = 1/4$,
$\;\;\;\;\;\;p_X(1) = P(X = 1) = 1/2$,
$\;\;\;\;\;\;p_X(2) = P(X = 2) = 1/4$,
且如果$x$取其他值, 则$p_X = 0$. -
$Y = 2 - X$, 表示反面朝上的次数. 有:
$\;\;\;\;P(Y=y) = P(2-X=y)=P(X=2-y)=p_x(2-y)$,
那么随机变量$Y$的概率质量函数为:
$\;\;\;\;\;\;p_Y(0) = P(Y = 0) = p_X(2) = 1/4$,
$\;\;\;\;\;\;p_Y(1) = P(Y = 1) = p_X(1) = 1/2$,
$\;\;\;\;\;\;p_Y(2) = P(Y = 2) = p_X(0) = 1/4$,
且如果$y$取其他值, 则$p_Y = 0$.
注意, 及时随机变量$X$和$Y$是不同的(映射方式不同), 但它们有相同的概率质量函数($p_X$和$p_Y$相同).
- $I$是表示第一次是是否正面朝上的 示性随机变量 . 因为$I(HT)=I(HH)=1, I(TH)=I(TT)=0$,
$\;\;\;\;\;\;p_I(0) = P(I=0) = 1/2$,
$\;\;\;\;\;\;p_I(1) = P(I=1) = 1/2$,
并且如果$I$取其他值, 那么$p_I = 0$.
$X、Y$和$I$的概率质量函数如下图 :
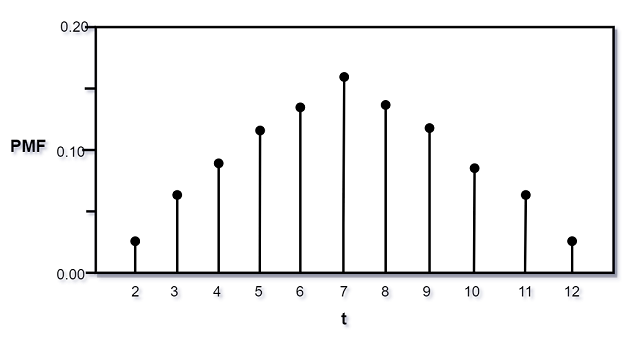
例 3.2.5 骰子点数之和
随机投掷两个6面骰子. 令$T=X+Y$表示两个骰子出现的点数之和, 其中$X$和$Y$是每个骰子分别出现的
点数, 该试验样本由36个等可能的结果组成:
$\;\;\;\;S = \lbrace (1,1),(1,2), \cdots (6,5),(6,6)\rbrace$.
因为骰子每个面均匀, 因此随机变量$X$的概率质量函数为
$\;\;\;\;\;\;P(X=j) = 1/6$,
其中, $j = 1,2,\cdots ,6$, 若$j$取其他值, $P(X=j)=0$. 我们称$X$在$1,2,\cdots ,6$上存在一个离散
均匀分布. $Y$与之相同.
注意, 虽然$X$和$Y$具有相同的分布, 但它们并不是相同的随机变量, 事实上,
$\;\;\;\;\;\;P(X = Y) = 6/36 = 1/6$
实际上, 与$X$具有相同分布的随机变量不止一个. 比如$7-X$(骰子的顶面和底面)和$7-Y$.
接着我们来计算$T$的PMF, 根据概率的朴素定义有:
$\;\;\;\;\;\;P(T = 2) = P(T = 12) = 1/36$,
$\;\;\;\;\;\;P(T = 3) = P(T = 11) = 2/36$,
$\;\;\;\;\;\;P(T = 4) = P(T = 10) = 3/36$,
$\;\;\;\;\;\;P(T = 5) = P(T = 9) = 4/36$,
$\;\;\;\;\;\;P(T = 6) = P(T = 8) = 5/36$,
$\;\;\;\;\;\;P(T = 7) = 6/36$.
如果$t$取其他值, $P(T = t) = 0$. 作为检验,
$\;\;\;\;P(T = 2) + P(T = 3) + \cdots + P(T = 12) = 1$,
说明我们考虑到了所有可能. 此例中$T$具有对称性: $P(T) = P(14 - T)$, 这是因为$X$和$7-X$具有相同
分布, $Y$和$7-Y$具有相同分布, 因此$T$和$14 - T$具有相同的分布.
随机变量$T$的概率质量函数如图:
接下来介绍一个与有效概率质量函数相关的性质.
定理 3.2.7 有效概率质量函数
设$X$是一个离散型随机变量, 且具有支撑$x_1,x_2,\cdots$(假设x_i的值不同, 且为表述简单, 设$X$的支撑是可数
无穷的; 如果支撑是有限的类似的结论也成立). 那么对于$X$的概率质量函数$P_X$必须满足下面2个标准:
-
非负性: $P(X=i)\ge 0, i = 0,1,2,\cdots$
-
归一性: $\sum_{j=1}^{\infty}P(X=x_j)=1$
证明: 由于概率是非负的, 因此第一个标准显然成立. 由于$X$必须在非负整数取值且事件$\lbrace X=x_j\rbrace$
之间独立, 因此有
$\;\;\;\;\sum_{j=1}^{\infty}P(X=x_j) = P(\bigcup_{j=1}^{\infty}\lbrace X=x_j\rbrace) = 1$
即第二个准则成立.
实际上, 上述两个准则是随机变量的概率质量函数的充要条件: 如果给定不同值$x_1,x_2,\cdots,$并且有一个函数
满足以上两条准则, 则这个函数是某个随机变量的PMF. 本书将在第5章介绍如何建立这样的随机变量.
PMF只是表达一个随机变量分布的方法之一. 一旦知道了$X$的PMF, 我们也可以通过对$x$的适当值进行求和
来计算$X$落入实数集中的给定子集的概率, 例如下面的例子.
例 3.2.8
回顾例 3.2.5 骰子点数之和, 设$T$表示两个骰子出现点数之和. 前面已计算过$T$的概率质量函数. 现假设
我们对$T$落入区间$[0, 4]$的概率很感兴趣, 由$T$的定义可知, 在区间内$T$只能取$2, 3, 4$. 根据PMF,有:
$\;\;\;\;P(1\le T\le 4) = P(T=2) + P(T=3) + P(T=4) = 6/36$
一般地, 给定一个离散型随机变量$X$和一个实数集$B$, 如果知道$X$的概率质量函数, 则通过对$X$的概率质量
函数图形在$B$中垂直点的高度进行求和, 可以得到$P(X\in B)$, 即$X$在$B$中的概率. 即根据一个随机变量的
概率质量函数, 可以确定它的分布.
3.3 伯努利分布和二项分布
在概率论与数理统计中, 一些分布是随处可见的, 以至于它们有固定的名称. 接下来将集中介绍有命名的分布,
这些分布在本书中贯穿始终. 从一个简单但有用的例子开始: 一个随机变量, 它只能取两个可能的值, 0或1.
定义 3.3.1 伯努利分布 bernoulli distribution
设$X$是一个随机变量, 如果满足$P(X=1)=p$且$P(X=0)=1-p$, 其中$0\lt p\lt 1$, 则称$X$是服从参数
为$p$的伯努利分布. 记作$X\sim Bern(p)$. 符号“$\sim$”读作“服从于”.
任何可能取值是0和1的随机变量都服从于一个$Bern(p)$分布, 其中$p$为随机变量取值为1的概率. $Bern(p)$
中的$p$称为分布的参数; 它可以确定出具体的伯努利分布. 即伯努利分布并不是唯一的, 而是存在由参数$p$
所标记的伯努利分布族. 例如, 假设$X\sim Bern(1/3)$, “$X$服从伯努利分布”这个说法虽然正确, 但却是
不完整的. 为完整描述$X$的分布, 需要同时说明分布的名称(伯努利分布)以及它的参数($1/3$), 二者均为
符号$X\sim Bern(1/3)$所包含的重要信息.
任何事件都会有一个伯努利随机变量, 因为这种随机变量是自然而然的存在于其中的, 如果事件发生则取值为1,
否则为0. 这种随机变量被称作 示性随机变量 . 之后我们会看到这种随机变量是非常有用的.

定义 3.3.2 示性随机变量
设$X$为随机变量, 如果事件$A$发生时取$X=1$, 否则$X=0$, 则称随机变量$X$为示性随机变量. 一般用符号$I_A$
或者$I(A)$表示事件$A$的示性随机变量. 有$I_A\sim Bern(P), p=P(A)$.
为方便理解, 人们经常用抛硬币的例子来想象伯努利随机变量.
案例 3.3.3 伯努利试验
进行一项随机试验, 若试验的结果只有“成功”或者“失败”, 则该试验为伯努利试验. 伯努利随机变量可以看作
是伯努利试验成功的标志: 如果成功, 则伯努利随机变量为1, 否则为0.
根据此试验, 参数$p$通常叫做伯努利分布的成功概率. 一旦开始考虑伯努利试验, 那么会很自然地考虑进行
多个伯努利试验的情形.
案例 3.3.4 二项分布 binomial distribution
假设进行$n$次独立的伯努利试验, 每次试验具有相同的成功概率$p$. 假设随机变量$X$表示试验成功的数量.
称$X$的分布具有参数$n$和$p$的二项分布. 符号$X\sim Bin(n,p)$表示$X$服从参数为$n$和$p$的二项分布,
其中$n$为正整数且$0\lt p\lt 1$.
需要注意的是, 这里没有用PMF定义二项分布, 而是通过案例描述了一种能产生服从二项分布的随机变量的
试验类型. 在统计学中, 最著名的哪些分布都是由案例的(example/story), 这些案例也解释了为什么它们
经常被用来当作数据模型, 或作为建立更复杂的分布的基础.
关于被命名的分布, 首先思考与它相关的案例会带来诸多好处. 它有助于模式识别(pattern recongnition),
使人们看清楚两个问题在本质上是同构的(相同结构/模式); 它还可以避免进行复杂的PMF计算, 给出更简洁
的解决方法. 此外, 它还能帮助我们了解分布之间是如何联系的. 显然上面所述的$Bern(p)$和$Bin(1,p)$是
一样的: 伯努利分布是二项分布的一个特例.
定理 3.3.5 二项分布的PMF
如果$X\sim Bin(n,p)$, 则$X$的概率质量函数为
$\;\;\;\;\;\;P(x=k) = \tbinom{n}{k}p^k(1-p)^{n-k}$,
其中, $k\in [0, n]$. 当$k$取其他值时, $P(X = k) = 0$.
-ω- 3.3.6
为节省篇幅, 在不指定非零的情况下, PMF通常为零. 但在任何情形中, 了解一个随机变量的支撑是什么
并且验证PMF的有效性是非常重要的. 如果有两个离散型随机变量具有相同的PMF, 则它们必须具有相同
的支撑. 因此有时一个离散型随机变量的支撑等价于这种分布的所有随机变量的支撑.
证明: (二项分布的PMF)
由$n$个相互独立的伯努利试验所组成的试验, 其结构由一系列的成功与失败组成, 由独立性包含$k$次成功
和$n-k$次失败的任意一个序列的概率为$p^k(1-p)^{n-k}$. 相同的序列需要在$n$次试验序列中选择哪些位置
是成功的, 这样的序列有$\tbinom{n}{k}$个. 因此, 设$X$为试验成功的次数, 有
$\;\;\;\;P(x = k) = \tbinom{n}{k}p^k(1-p)^{n-k}$,
其中, $k\in [0, n]$, 当$k$取其他值时, $P(X=k) = 0$. 因为概率非负, 且由二项式定理:
$\;\;\;\;\sum_{k=0}^{n}\tbinom{n}{k}p^k(1-p)^{n-k} = (p+(1-p))^n = 1$,
因此该PMF是有效的(valid). (证明过程说明了分布名称的由来).
下面是两个不同参数时的二项分布的PMF图:
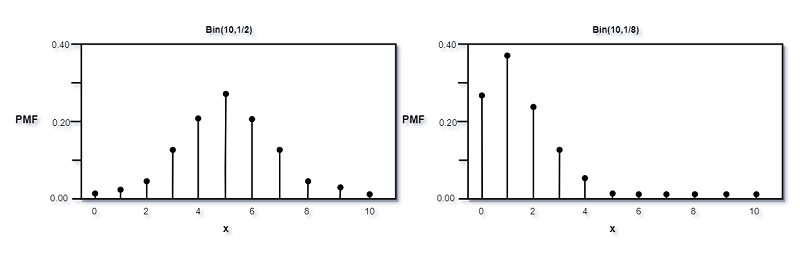
当$p=1/2$时, PMF图是对称的, 否则是倾斜的. 对于所有的PMF图像, 所有垂直点高度和为1.
下面将说明如果$X$服从二项分布, 则$n - X$也服从二项分布.
定理 3.3.7
设$X\sim Bin(n,p)$, 且$q = 1 - p$(用$q$表示伯努利试验失败的概率), 则$n-X\sim Bin(n,q)$.
证明: 借用二项分布的案例, 将$X$解释为进行$n$次独立伯努利试验成功的次数, 则$n-X$就表示试验
失败的次数. 类似兑对称性, 互相交换成功与失败的角色(将成功和失败的标记交换), 可以得到$n-X\sim Bin(n,q)$.
或者从PMF出发利用代数证明: 设$Y = n - X$, 则$Y$的PMF为:
$\;\;\;\;P(Y=k) = P(n-X=k) = P(X=n-k) = \tbinom{n}{n-k}p^{n-k}q^k = \tbinom{n}{n-k}q^kp^{n-k}$
其中$k\in [0,n]$.
推论 3.3.8
设$X\sim Bin(n,p)$, 其中$n$为偶数, $p = 1/2$, 则$X$的分布是关于$n/2$对称的, 也就是对于所以非负整数$j$,
都有$P(X=\frac{n}{2}+j) = P(X=\frac{n}{2}-j)$.
证明: 由定理 3.3.7可知, $n - X$同样服从$X\sim Bin(n,1/2)$, 因此对于所有非负整数$k$, 有
$\;\;\;\;P(X=k) = P(n-X=k) = P(X=n-k)$,
令$k = n/2 + j$即可得证.
例 3.3.9 抛硬币续
回顾例 3.1.2 抛硬币, 有$X\sim Bin(2,1/2), Y\sim Bin(2,1/2), I\sim Bern(1/2)$. 由定理3.3.7,
$X$和$Y$具有相同的分布; 再根据推论 3.3.8, 可知$X$和$Y$的分布是关于$1$对称的.
3.4 超几何分布 hypergeometric distribution
假设有一个由$w$个白球和$b$个黑球充满的罐子, 然后 有放回 地从罐子里随机抓取$n$个球, 以这$n$个球
中白球的数量作为随机变量, 由于每次抓取的过程相当于独立的伯努利试验(试验成功的概率为$\frac{w}{w+b}$),
因此该变量服从参数为$n$和$\frac{w}{w+b}$的二项分布. 如果现在改成 不放回 地从罐子里随机抓取$n$
个球, 则白球的数量会服从 超几何分布 .
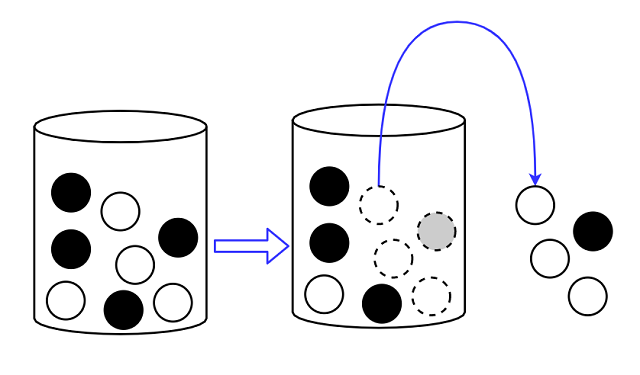
案例 3.4.1 超几何分布
考虑一个由$w$个白球和$b$个黑球充满的罐子. 现在随机不放回地从罐子中抓取$n$个小球, 共有$\tbinom{w+b}{n}$
种不同方案, 且每个方案等可能. 设$X$表示$n$个球中白球的数量, 则称$X$服从参数为$w、b$和$n$的超几何分布.
记作$X\sim HGeom(w,b,n)$.
如同二项分布, 同样可以从案例中得到超几何分布.
定理 3.4.2 超几何分布的PMF
如果$X\sim HGeom(w,b,n)$, 则X的概率质量函数为
$\;\;\;\;\;\;P(X=k) = \frac{\tbinom{w}{k}\tbinom{b}{n-k}}{\tbinom{w+b}{n}}$,
对于满足$0\le k\le w$且$0\le n-k\le b$的所有正整数$k$均成立, 并且当$k$取其他值时, $P(X=k) = 0$.
证明: 为了得到$P(X=k)$, 首先要计算出恰好取出$k$个白球和$n - k$个黑球的方法数量(区分每个球(label),
不区分顺序). 如果$k\gt w$或者$n - k\gt b$, 则该情况不成立; 否则根据乘法法则, 恰好取出$k$个白球和$n$个
黑球的方法有$\tbinom{w}{k}\tbinom{b}{n - k}$种, 而从罐子中取出$n$个球的方法有$\tbinom{w + b}{n}$种.由于所有选择是等可能的, 由概率的朴素定义, 有
$\;\;\;\;P(X=k) = \frac{\tbinom{w}{k}\tbinom{b}{n - k}}{\tbinom{w + b}{n}}$
上式对满足$0\ge k\ge w$且$0\ge n - k\ge b$的所有正整数$k$均成立. 根据范德蒙(Vandermonde, 例 1.5.3),
有$\sum_{k = 1}{n}\tbinom{w}{k}\tbinom{b}{n - k} = \tbinom{w + b}{n}$, 故PMF之和为1, 所以$X$的概率质量函数是有效的.
超几何分布出现在许多情况下. 超几何分布的适用基础是总体根据2套标签进行分类, 在罐子的示例中:
每个球不是黑色就是白色(第1套标签); 每个球要么是样本(被取出)要么不是样本(第2套标签). 此外,
这些标签至少有一个是被完全随机分配的(在罐子的例子中, 球是被随机抽样的). 那么$X\sim HGeom(w,b,n)$
代表被两套标签都标记的数量: 在罐子的例子中, 关注的是即被抽样(取出)又是白色的球.
接下来介绍的两个例子看似是不同场景, 但本质上它们是与罐子示例是同构的.
例 3.4.3 麋鹿的捕获-再捕获
森林中有$N$头麋鹿. 某天, 共捕获了$m$头麋鹿, 做标记后将这$m$头麋鹿同时释放回野外. 几天后, 又
重新随机地捕获$n$头麋鹿. 假设重新随机地捕获$n$头麋鹿也同样可能是之前捕获的麋鹿.

由前面介绍的超几何分布的案例可知, 再次被捕获的麋鹿的数量服从参数为$m、N - m$和$n$的超几何分布
$HGeom(m, N-m, n)$. 第一次捕获的麋鹿相当于白球; 未捕获的相当于黑球; 在此被捕获的相当于抽样.
例 3.4.4 扑克牌中的老A数
从一副充分洗好的标准扑克牌中随机抽取5张, 在抽取的牌中, A牌的数量服从参数为$4、48$和$5$的
超几何分布$HGeom(4,48,5)$, 这里可以把A看作白球, 其他牌看作黑球.
下标对上述示例如何看作是“总体按两套标签进行区分”进行了总结. 在每个例子中, 我们感兴趣的随机变量是
落入第2列和第4列的数: 白球且被抽到; 捕获且再被捕获; A牌且在手中.

定理 3.4.5
超几何分布$HGeom(w, b, n)$和$HGeom(n, w + b - n, w)$是等价的. 换句话说, 如果$X\sim HGeom(w, b, n)$
且$Y\sim HGeom(n, w + b - n, w)$, 那么$X$和$Y$是同分布的.
证明: 借用罐子的例子, 考虑一个由$w$个白球和$b$个黑球充满的罐子. 现在随机地不放回地从罐子里
抓取$n$个球. 假设$X$表示抽取样本中白球的数量, 有$X\sim HGeom(w, b, n)$. 在这个例子中, 白球或
黑球被当作第1套标签; 是否被抽取作为第2套标签. 类似地, 假设$Y\sim HGeom(n, w + b - n, w)$也
表示抽取样本中白球的数量, 此时是否被抽取作为第1套标签; 是否是白球作为第2套标签. 即$X$和$Y$都
表示被抽取的白球的数量, 所以它们具有相同分布.
-ω- 3.4.6 二项分布vs超几何分布
二项分布和超几何分布往往容易令人混淆. 它们都是在整数$0\sim N$之前取值的离散型分布, 并且它们都可以
解释为伯努利试验成功的次数(对于超几何分布, 抽取一个白球可以看作是一次成功). 然而, 一个关键点在于,
二项分布的案例中每次伯努利试验是独立的, 而超几何分布中每次伯努利分布不是, 这是由不放回地抽样所引起
的: 已知被抽取的一个球是白色, 则另一个也是白色的概率会减小.
3.5 离散型均匀分布 discrete uniform distribution
接下来将介绍一个简单案例, 这个案例和概率的朴素定义密切相关—从有限集里选择一个随机数.
案例 3.5.1 离散均匀分布
设$C$是一个非空且有限的数字集合. 随机且均匀地从$C$中选择一个数(即$C$中每个数被抽取的可能性相等). 将
被抽取的数记为$X$, 则称$X$服从参数为$C$的 离散均匀分布 , 记为$X\sim DUnif(C)$. $X$的PMF为:
$\;\;\;\;\;\;P(X = x) = \frac{1}{|C|}$
上式对满足$x\in C$的$x$均成立(否则为$0$). 特别的, 对于$X\sim DUnif(C)$以及$A\in C$, 有
$\;\;\;\;\;\;P(X\in A) = \frac{|A|}{|C|}$.
例 3.5.2 随机纸条
一顶帽子🧢中放有100张纸条, 每张纸条都由数字$1, 2, \cdots , 100$中的一个数字进行标记且每张
纸条的数字不重复. 现在抽取5张纸条.
-
首先考虑放回抽样(等概率).
(a)抽取的纸条中, 标记数字大于等于80的纸条个数的分布是什么?(b)第$j$张纸条上标记的数字的分布是什么?($1\le j\le 5$)(c)数字100至少被抽中一次的概率是多少?
-
接着考虑不放回抽样(
5张牌的各种组合是等可能出现的).(d)抽取的纸条中, 标记数字大于等于80的纸条个数的分布是什么?(e)第$j$张纸条上标记的数字分布是什么?($1\le j\le 5$)(f)数字100至少被抽中一次的概率是多少
解:
$\;\;\;\;$(a) 由二项分布的案例(story)可知, 该问题的分布是$Bin(5, 0.21)$.
$\;\;\;\;$(b) 设$X_j$为第$j$张纸条上标记的数字, 事件相互独立, $X_j\sim DUnif(1,2,\cdots ,100)$
$\;\;\;\;$(c) 考虑该事件的补集(对立事件),
$\;\;\;\;\;\;\;\; P(X_j = 100至少存在一个j) = 1 - P(X_1\not= 100, X_2\not= 100, …, X_5\not= 100)$,
由概率的朴素定义, 上式等于$1 - (99/100)^5\approx 0.049$
对于上式我们需要解释为什么$P(X_1\not= 100, X_2\not= 100, …, X_5\not= 100) = P(X_1\not= 100)\times … \times P(X_5\not= 100)$
这涉及随机变量的独立性进行推导, 相关概念将在3.8节中详细介绍.
$\;\;\;\;$d 由超几何分布的案例, 该问题的分布是$HGeom(21, 79, 5)$.
$\;\;\;\;$设$Y_j$为第$j$张纸条上标记的数字, 由对称性知, $Y_j\sim DUnif(1, 2, …, 100)$. 其中$Y_j$
之间不是相互独立的(详见3.8节), 但由于在无条件情况下, 对于所有纸条而言, 第$j$个被抽中可能性相等,
因此对称性仍然成立.
$\;\;\;\;$(f) 由于现在是不放回抽样, 因此事件$Y_1 = 100, Y_2 = 100, …, Y_5 = 100$是不独立的, 所以有
$\;\;\;\;\;\;\;\; P(Y_j = 100至少有一个j) = P(Y_1 = 100) + … + P(Y_5 = 100)$.
完整性检查:直观上答案是合理的, 这是因为我们也可以认为, 先从$100$张空白的纸条中随机选$5$张,
然后在这些纸条上从$1$到$100$随机写一个数字, 有$5/100$的可能性这$5$张纸条中出现数字100. 或者
可以用代数的方式理解: $P = \frac{\tbinom{99}{4}}{\tbinom{100}{5}}$
如果(c)结果大于(f)的结果将是非常奇怪的, 这是因为在不放回抽样中抽中数字100的纸条更容易些.
(抽不是100的纸条会增加之后抽中100的可能性). 但有意思的是, (c)的结果只是比(f)的结果略低
一点, 这是由于同样的纸条被抽中超过一次的可能性是非常小的.

