本文章原出处：chicago01.top，转载不需说明，随意转载

简单栈

栈是一种“先进先出”的数据结构，栈只有一端可以进出元素，我们称这一端为栈顶。添加和删除元素时我们只能对栈顶进行操作。

[HTML_REMOVED]

实现方式可以用数组或者STL中的stack。

//数组实现栈
int stk[N];
// 这里使用 stk[0]( 即 *stk ) 代表栈中元素数量，同时也是栈顶下标
// 压栈 ：
stk[++*stk] = var1;
// 取栈顶 ：
int u = stk[*stk];
// 弹栈 ：注意越界问题, *stk == 0 时不能继续弹出
if (*stk) --*stk;
// 清空栈
*stk = 0;

//STL中stack
#include <stack>
#include <iostream>
using namespace std;
int main()
{
    // 创建堆栈对象
    stack<int> s;
    // 元素入栈
    s.push(3);
    s.push(19);
    s.push(23);
    s.push(36);
    s.push(50);
    s.push(4);

    cout << s.size() << endl;
    // 元素依次出栈
    while(!s.empty())
    {
        // 打印栈顶元素，打印出：4 50 36 23 19 3
        cout << s.top() << endl;
        // 出栈
        s.pop();
    }

    return 0;
}

【例题】 Push，Pop，GetMin

设计一个支持push，pop，top等操作并且可以在O(1)时间内检索出最小元素的堆栈。

题解

我们用两个栈来维护，MinStack 和 NumStack。

在入栈时，NumStack正常入栈，而MinStack则入栈当前已知最小数。

当GetMin时，只需要返回MinStack栈顶元素。

出栈时NumStack 和 MinStack 同时出栈。

代码演示

交互题，无样例代码。

【例题】 火车进出栈

这里有n列火车将要进站再出站，但是，每列火车只有1节，那就是车头。

这n列火车按1到n的顺序从东方左转进站，这个车站是南北方向的，它虽然无限长，只可惜是一个死胡同，而且站台只有一条股道，火车只能倒着从西方出去，而且每列火车必须进站，先进后出。

也就是说这个火车站其实就相当于一个栈，每次可以让右侧头火车进栈，或者让栈顶火车出站。

车站示意如图：

            出站<——    <——进站
                     |车|
                     |站|
                     |__|

现在请你按《字典序》输出前20种可能的出栈方案。

输入格式

输入一个整数n，代表火车数量。

输出格式

按照《字典序》输出前20种答案，每行一种，不要空格。

数据范围

$1≤n≤20$

输入样例：

3

输出样例：

123
132
213
231
321

题解

由题目可以知道，火车栈存在两种情况，要么出栈，要么进栈。

于是我们模拟一下样例：

n = 3
第一种情况：
    1. 1 进栈
    2. 1 出栈
    3. 2 进栈
    4. 2 出栈
    5. 3 进栈
    6. 3 出栈
    输出顺序：1 2 3
第二种情况：
    1. 1 进栈
    2. 1 出栈
    3. 2 进栈
    4. 3 进栈
    5. 3 出栈
    6. 2 出栈
    输出顺序：1 3 2
······

代码演示

//官方代码
#include <cstdio>
#include <iostream>
using namespace std;
const int N = 26;
int n, num = 0, st[N], top = 0, ans[N], t = 0;

void z(int x) {
    if (x == n + 1) {
        if (++num > 20) exit(0);
        for (int i = 1; i <= t; i++) printf("%d", ans[i]);
        for (int i = top; i; i--) printf("%d", st[i]);
        cout << endl;
        return;
    }
    if (top) {
        ans[++t] = st[top--];
        z(x);
        st[++top] = ans[t--];
    }
    st[++top] = x;
    z(x + 1);
    --top;
}

int main() {
    cin >> n;
    z(1);
    return 0;
}

表达式计算

表达式分为前缀、中缀、后缀表达式。

我们平时生活中和数学中用的都是中缀表达式，形如 $2*(9-1)$ 。

而前缀表达式又称波兰式，形如 $op A B$ ，$op$ 是要对$A B$进行的运算的运算符号。

同上，后缀表达式就是，形如 $AB$ $ op$ ，$op$ 是要对$A B$进行的运算的运算符号。

后缀表达式求值计算

1. 建立一个栈
2. 遇到数字就进栈
3. 遇到运算符，取出栈顶的两个元素，进行运算后压入栈中
4. 当栈中只剩下一个元素，就是答案

// 后缀表达式转中缀表达式，同时求值，O(n)

// 数值栈 
vector<int> nums; 
// 运算符栈 
vector<char> ops;

// 优先级 
int grade(char op) {
    switch (op) {
    case '(':
        return 1;
    case '+':
    case '-':
        return 2;
    case '*':
    case '/':
        return 3;
    }
    return 0;
}

// 处理后缀表达式中的一个运算符 
void calc(char op) {
    // 从栈顶取出两个数 
    int y = *nums.rbegin();
    nums.pop_back();
    int x = *nums.rbegin();
    nums.pop_back();
    int z;
    switch (op) {
    case '+':
        z = x + y;
        break;
    case '-':
        z = x - y;
        break;
    case '*':
        z = x * y;
        break;
    case '/':
        z = x / y;
        break;
    }
    // 把运算结果放回栈中 
    nums.push_back(z);  
}

单调栈

单调栈顾名思义，就是栈中元素呈现单调性。

插入

将一个元素插入单调栈时，为了维护栈的单调性，需要在保证将该元素插入到栈顶后整个栈满足单调性的前提下弹出最少的元素。

例如，栈中自顶向下的元素为 ，插入元素 时为了保证单调性需要依次弹出元素 ，操作后栈变为 。

用伪代码描述如下：

/*
* 本伪代码对应的是单调递减栈 
*共n个元素，编号为0~n-1
*/
while(栈为空) 栈顶元素出栈; //先清空栈
a[n]=-1;
for(i=0;i<=n;i++)
{
    if(栈为空或入栈元素大于等于栈顶元素) 入栈;
    else 
    {
        while(栈非空并且栈顶元素大于等于入栈元素)
        {
            栈顶元素出栈;
            更新结果; 
        } 
        将最后一次出栈的栈顶元素（即当前元素可以拓展到的位置）入栈; 
        更新最后一次出栈的栈顶元素其对应的值; 
    }    
}
输出结果; 

使用

自然就是从栈顶读出来一个元素，该元素满足单调性的某一端。

例如举例中取出的即栈中的最小值。

【例题】 直方图中最大矩形

直方图是由在公共基线处对齐的一系列矩形组成的多边形。

矩形具有相等的宽度，但可以具有不同的高度。

例如，图例左侧显示了由高度为2,1,4,5,1,3,3的矩形组成的直方图，矩形的宽度都为1：

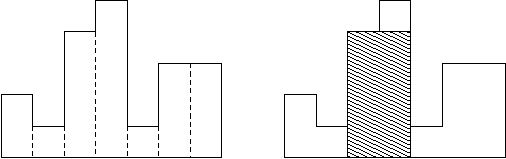
通常，直方图用于表示离散分布，例如，文本中字符的频率。

现在，请你计算在公共基线处对齐的直方图中最大矩形的面积。

图例右图显示了所描绘直方图的最大对齐矩形。

输入格式

输入包含几个测试用例。

每个测试用例占据一行，用以描述一个直方图，并以整数n开始，表示组成直方图的矩形数目。

然后跟随n个整数$h_1，…，h_n$。

这些数字以从左到右的顺序表示直方图的各个矩形的高度。

每个矩形的宽度为1。

同行数字用空格隔开。

当输入用例为n=0时，结束输入，且该用例不用考虑。

输出格式

对于每一个测试用例，输出一个整数，代表指定直方图中最大矩形的区域面积。

每个数据占一行。

请注意，此矩形必须在公共基线处对齐。

数据范围

$1≤n≤100000$,
$0≤hi≤1000000000$

输入样例：

7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0

输出样例：

8
4000

题解

其实这是一道贪心+单调栈的题目。

只需要证明所选矩形里面的直方条是单调增的，这时候就变成求单调栈的问题了。其答案就是每次弹出一个高度就计算一下面积，取最大值。

代码演示

//官方标程
#include<iostream>
#include<cstdio>
#include<cstring> 
#include<algorithm>
using namespace std;
int n,p;
int a[100010];
int s[100010],w[100010];
long long ans;

int main()
{
    while(cin>>n&&n)
    {
        ans=0; p=0;
        for(int i=1;i<=n;i++) scanf("%d",&a[i]);
        a[n+1]=0;
        for(int i=1;i<=n+1;i++)
        {
            if(a[i]>s[p]) s[++p]=a[i],w[p]=1;
            else{
                int width=0;
                while(s[p]>a[i])
                {
                    width+=w[p];
                    ans=max(ans,(long long)width*s[p]);
                    p--;
                }
                s[++p]=a[i],w[p]=width+1;
            }
        }
        cout<<ans<<endl;
    }
}