正常发挥。。。
1题正常过，2题想出解法后bfs遍历偏移量错了4写成了n，wa了一发，还好及时更正了。
3题据说是结论题，一顿特判7/12wa了
看y总视频，得打表找规律
博弈论好难，有聚聚能推荐个什么题单或总结的博客吗QAQ
排名可能就在五百上下波动了，得继续学习
T1
排个序，倒着判定就行，注意sqrt函数的参数不能是负数

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
int n,a[100010];
int b(int x){
    return (int)sqrt(x);
}
int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++ ){
        cin>>a[i];
    }
    sort(a+1,a+1+n);
    for (int i=n;i>=1;i--){
        if (a[i]<0){
            printf ("%d\n",a[i]);
            return 0;
        }
        else {
            int u=b(a[i]);
            if (u*u!=a[i]){
                printf ("%d\n",a[i]);
                return 0;   
            }
        }
    }
    return 0;
}

T2
bfs出所有起点能到的点，所有能到终点的。
都存下，然后二重循得到这两个组的建立传送门的最低费用。
如果有从起点走到终点不用建门的情形，最低费用也会计算出0，不用特判。

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#define x first
#define y second
using namespace std;
typedef pair<int, int> pii;
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};//偏移量数组
int n,lx,ly,rx,ry;
char g[60][60];
bool st[60][60];
int key;
vector <pii> q;
int hh,tt;
void bfs(int ax,int ay){
    q.push_back({ax,ay});
    st[ax][ay]=1;
    hh=tt=0;
    while (hh<=tt){//此处是数组模拟队列
        auto t=q[hh++];
        for (int i = 0; i < 4; i ++ ){
            int nx,ny;
            nx=t.x+dx[i],ny=t.y+dy[i];
            if (nx>=1&&nx<=n&&ny>=1&&ny<=n&&
            g[nx][ny]=='0'&&st[nx][ny]==0){
                st[nx][ny]=1;
                q.push_back({nx,ny});
                tt++;
            }
        }
    }
    return ;
}
int main()
{
    scanf("%d", &n);
    cin>>lx>>ly>>rx>>ry;
    if (lx==rx&&rx==ry) {//如果出生在终点 特判0
        puts("0");
        return 0;
    }
    for (int i = 1; i <= n; i ++ ){
        scanf ("%s",g[i]+1);
    }
    vector <pii> a,b;//a存起点可到的点 b存可到终点的点
    bfs(lx,ly);
    a=q;
    q.clear();
    memset(st, 0, sizeof st);
    bfs(rx,ry);
    b=q;
    int ans=1e9;
    for (auto i:a){
        for (auto j:b){
            ans=min(ans,(i.x-j.x)*(i.x-j.x)+(i.y-j.y)*(i.y-j.y));
        }
    }
    printf ("%d\n",ans);
    return 0;
}

T3
放上 灵茶山艾府 大佬的题解
分类讨论

首先，对于k=3的情况，只能取1或2或3个石头，那么此情形就是一个标准的巴什博弈

巴什博弈：有一堆总数为n的物品，2名玩家轮流从中拿取物品。每次至少拿1件，至多拿m件，不能不拿，最终将物品拿完者获胜。
结论就是若n%(m+1)==0则后手必胜，否则先手必胜

1. 对于n<k的情况，只能取1或2个石头，那么此情形也是一个标准的巴什博弈，套结论判断若n%(2+1)等于0则后手必胜，否则先手必胜。

2. 对于n>k的情况,我们对于k进行分类讨论

   • 情形A:k%3!=0
     • 若n是3的倍数，先手无论是取1，2，k，后手都能让先手面临的情形变为n%3=0，如此反复拉扯，进入n<k的情形。在n<k的情况下，若n%(2+1)等于0则后手必胜，否则先手必胜。所以对于k%3!=0&&n%3==0的情况，先手每局都面对n%3==0的情况，所以结局就是后手必胜。
     • 若n不是3的倍数，先手若使后手面临n是3的倍数的情况，根据上面的推断，那么他就必胜。所以对于k%3!=0&&n%3!=0的情况,结论就是先手必胜。
   • 情形B:k%3==0
     在用SG函数打表后发现如下规律，对于k%3的情况，胜负情况每(k+1)一个循环，也就是说，若k=9， n=100的结果与n=10的结果是一样的。
     所以，若k%3==0，则结果与n%=(k+1)的结果一致。
     n%=(k+1)的情形有二种
     • n=k此情形先手必胜
     • n<k 此情形套结论判断，若n%(2+1)等于0则后手必胜，否则先手必胜。

最终，我们发现

1. 对于k%3!=0的情况，n<k与n>k的情况可合并，判断若n%(2+1)等于0则后手必胜，否则先手必胜。
2. 对于k%3==0的情况, n=k此情形先手必胜,n<k与n>k的情况可合并，判断若n%(2+1)等于0则后手必胜，否则先手必胜。

下面放上ac代码

#include <iostream>
#include <cstring>
#include <algorithm>
#include <set>
#define c continue
using namespace std;
int T,n,k;
int main(){
    scanf("%d", &T);
    while (T--){
        scanf("%d%d", &n, &k);
        if (k%3){//对于k%3!=0的情况，n<k与n>k的情况可合并
            if (n%3) puts("Alice");//判断若n%(2+1)等于0则后手必胜，否则先手必胜。
            else puts("Bob");
        }
        else {
            n%=k+1;//对于k%3==0的情况, n<k与n>k的情况可合并,n与n%(k+1)的结果相同
            if (n==k||n%3) puts("Alice");//n==k此情形先手必胜胜，否则先手必胜。
            else puts("Bob");//若不相等，判断若n%(2+1)，等于0则后手必
        }
    }
    return 0;
}

下面放上打表结果图

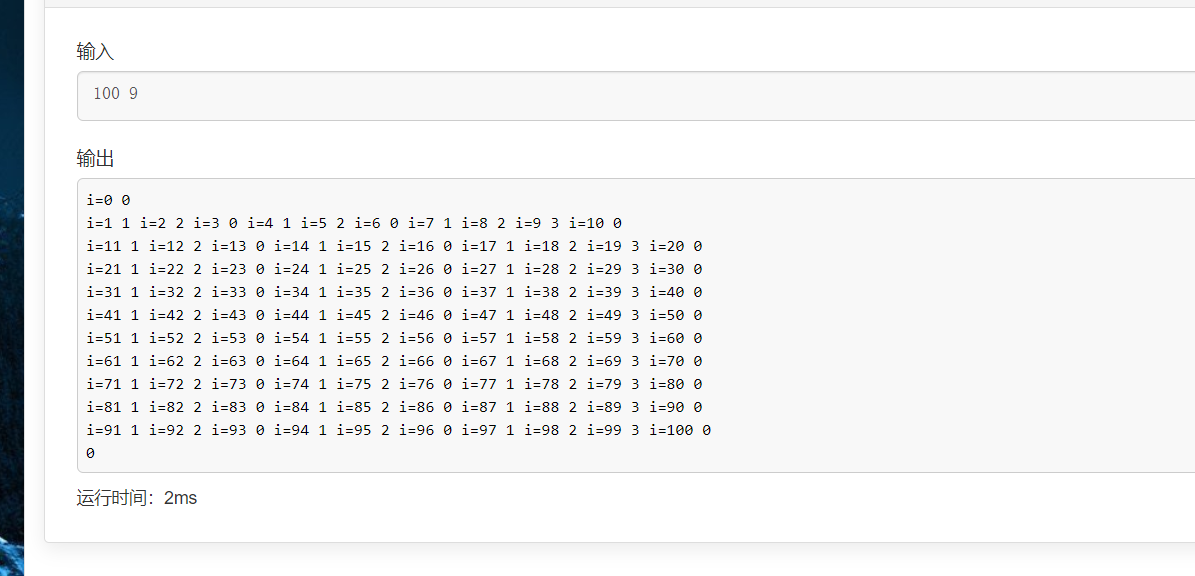
同时放出打表的代码 sg函数的原理及使用见AcWing 893. 集合-Nim游戏

//此为 打表的代码 ac代码在上面
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>
#include <string.h>
#include <cmath>
#include <set>
using namespace std;
int n,k;
int sg[10010];
int SG(int x){
    if (sg[x]!=-1) return sg[x];
    set <int> S;
    int d[]={1,2,k};
    for (int i=0;i<3;i++){
        if (x>=d[i]){
            S.insert(SG(x-d[i]));
        }
    }
    for (int i=0;;i++){
        if (!S.count(i)){
            return sg[x]=i;
        }
    }
}
int main(){
    cin>>n>>k;
    memset(sg, -1, sizeof sg);
    sg[0]=0;
    for (int i=0;i<=n;i++){
        printf ("i=%d ",i);
        cout<<SG(i)<<' ';
        if (i%(k+1)==0) cout<<'\n';
    }
    cout<<SG(n%(k+1));
    return 0;
}