DFS 最重要的是搜索顺序。用什么顺序遍历所有方案。

全排列展示DFS过程

我们用DFS来解决全排列问题看看它的过程，以 n = 3 为例，可以这样进行搜索：

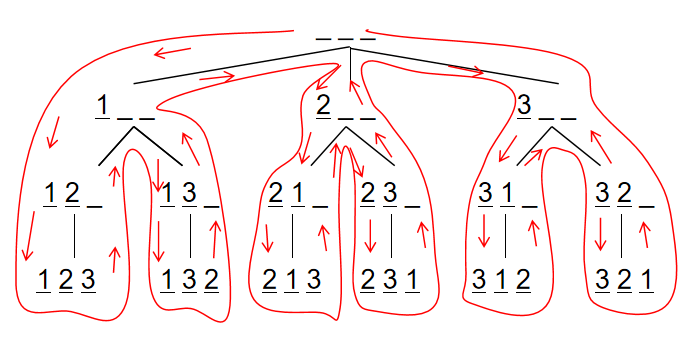
假设有 3 个空位，从前往后填数字，每次填一个位置，填的数字不能和前面一样。

最开始的时候，三个空位都是空的： __

首先填写第一个空位，第一个空位可以填 1，填写后为：1

填好第一个空位，填第二个空位，第二个空位可以填 2，填写后为：1 2 __

填好第二个空位，填第三个空位，第三个空位可以填 3，填写后为： 1 2 3

这时候，空位填完，无法继续填数，所以这是一种方案，输出。

然后往后退一步，退到了状态：1 2 __ 。剩余第三个空位没有填数。第三个空位上除了填过的 3 ，没有其他数字可以填。

因此再往后退一步，退到了状态：1 。第二个空位上除了填过的 2，还可以填 3。第二个空位上填写 3，填写后为：1 3 __

填好第二个空位，填第三个空位，第三个空位可以填 2，填写后为： 1 3 2

这时候，空位填完，无法继续填数，所以这是一种方案，输出。

然后往后退一步，退到了状态：1 3 __ 。剩余第三个空位没有填数。第三个空位上除了填过的 2，没有其他数字可以填。

因此再往后退一步，退到了状态：1 。第二个空位上除了填过的 2，3，没有其他数字可以填。

因此再往后退一步，退到了状态： 。第一个空位上除了填过的 1，还可以填 2。第一个空位上填写 2，填写后为：2 __

填好第一个空位，填第二个空位，第二个空位可以填 1，填写后为：2 1 __

填好第二个空位，填第三个空位，第三个空位可以填 3，填写后为：2 1 3

这时候，空位填完，无法继续填数，所以这是一种方案，输出。

然后往后退一步，退到了状态：2 1 __ 。剩余第三个空位没有填数。第三个空位上除了填过的 3，没有其他数字可以填。

因此再往后退一步，退到了状态：2 。第二个空位上除了填过的 1，还可以填 3。第二个空位上填写 3，填写后为：2 3 __

填好第二个空位，填第三个空位，第三个空位可以填 1，填写后为：2 3 1

这时候，空位填完，无法继续填数，所以这是一种方案，输出。

然后往后退一步，退到了状态：2 3 __ 。剩余第三个空位没有填数。第三个空位上除了填过的 1，没有其他数字可以填。

因此再往后退一步，退到了状态：2 。第二个空位上除了填过的 1，3，没有其他数字可以填。

因此再往后退一步，退到了状态： 。第一个空位上除了填过的 1，2，还可以填 3。第一个空位上填写 3，填写后为：3 __

填好第一个空位，填第二个空位，第二个空位可以填 1，填写后为：3 1 __

填好第二个空位，填第三个空位，第三个空位可以填 2，填写后为：3 1 2

这时候，空位填完，无法继续填数，所以这是一种方案，输出。

然后往后退一步，退到了状态：3 1 __ 。剩余第三个空位没有填数。第三个空位上除了填过的 2，没有其他数字可以填。

因此再往后退一步，退到了状态：3 。第二个空位上除了填过的 1，还可以填 2。第二个空位上填写 2，填写后为：3 2 __

填好第二个空位，填第三个空位，第三个空位可以填 1，填写后为：3 2 1

这时候，空位填完，无法继续填数，所以这是一种方案，输出。

然后往后退一步，退到了状态：3 2 __ 。剩余第三个空位没有填数。第三个空位上除了填过的 1，2，没有其他数字可以填。

因此再往后退一步，退到了状态：3 。第二个空位上除了填过的 1，2，没有其他数字可以填。

因此再往后退一步，退到了状态： __。第一个空位上除了填过的 1，2，3，没有其他数字可以填。

此时深度优先搜索结束，输出了所有的方案.

>算法：

• 用 path 数组保存排列，当排列的长度为 n 时，是一种方案，输出

• 用 state 数组表示数字是否用过。当 state[i] 为 1 时：i 已经被用过，state[i] 为 0 时，i 没有被用过。

• dfs(i) 表示的含义是：在 path[i] 处填写数字，然后递归的在下一个位置填写数字

• 回溯：第 i 个位置填写某个数字的所有情况都遍历后， 第 i 个位置填写下一个数字

#include<iostream>
using namespace std;
const int N = 10;
int path[N];//保存序列
int state[N];//数字是否被用过
int n;
void dfs(int u)
{
    if(u > n)//数字填完了，输出
    {
        for(int i = 1; i <= n; i++)//输出方案
            cout << path[i] << " ";
        cout << endl;
    }

    for(int i = 1; i <= n; i++)//空位上可以选择的数字为:1 ~ n
    {
        if(!state[i])//如果数字 i 没有被用过
        {
            path[u] = i;//放入空位
            state[i] = 1;//数字被用，修改状态
            dfs(u + 1);//填下一个位
            state[i] = 0;//回溯，取出 i
        }
    }
}
//时间复杂度为 O(n*n!)
//空间复杂度为 O(n)

DFS就像愣头青，不回头搜索，到底后回溯！

但是我们可以通过条件的判断，实现剪枝，从而提高算法效率：

经典n皇后问题

下面以八皇后为例：

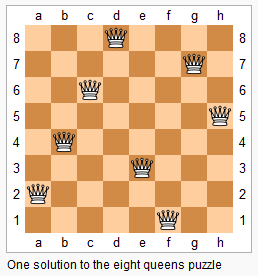
在皇后的每行每列每对角线上，不能有其他皇后存在，就类似于一个全排列问题，我们可以把所以全部枚举判断。也可以
在过程中剪枝，以极大提高效率：
算法一：按行枚举 时间复杂度O(n!)

分析:

对角线 dg[u+i]dg[u+i] ，反对角线udg[n−u+i]udg[n−u+i]中的下标 u+iu+i和 n−u+in−u+i 表示的是截距，col表示的是列（因为按行搜索，不用在判断行了）。
以x，y表示u,i分析如下：

1. 图看成坐标系，正反对角线 y=x+b y=-x+b, 截距 b=y−x b=y+x，在b=y-x时因为我们要把 b 当做数组下标来用，显然 b 不能是负的，所以我们加上 +n （实际上+n+4,+2n都行），来保证是结果是正的，即 y - x + n
2. u，i不用分特别清楚谁是x，谁是y，能特定分清楚对角线即可，即使代码中u，i互换一样AC

代码:

#include <iostream>
using namespace std;
const int N = 20; 

// bool数组用来判断搜索的下一个位置是否可行
// col列，dg对角线，udg反对角线
// g[N][N]用来存路径

int n;
char g[N][N];
bool col[N], dg[N], udg[N];

void dfs(int u) {
    // u == n 表示已经搜了n行，故输出这条路径
    if (u == n) {
        for (int i = 0; i < n; i ++ ) puts(g[i]);   // 等价于cout << g[i] << endl;
        puts("");  // 换行
        return;
    }

    //对n个位置按行搜索
    for (int i = 0; i < n; i ++ )
        // 剪枝(对于不满足要求的点，不再继续往下搜索)  
        // udg[n - u + i]，+n是为了保证下标非负
        if (!col[i] && !dg[u + i] && !udg[n - u + i]) {
            g[u][i] = 'Q';
            col[i] = dg[u + i] = udg[n - u + i] = true;
            dfs(u + 1);
            col[i] = dg[u + i] = udg[n - u + i] = false; // 恢复现场 这步很关键
            g[u][i] = '.';

        }
}

int main() {
    cin >> n;
    for (int i = 0; i < n; i ++ )
        for (int j = 0; j < n; j ++ )
            g[i][j] = '.';

    dfs(0);

    return 0;
}   

算法二：DFS按每个元素枚举 时间复杂度O(2n2)
每个位置两种情况，n2个位置

// 不同搜索顺序 时间复杂度不同  所以搜索顺序很重要！
#include <iostream>
using namespace std;
const int N = 20;

int n;
char g[N][N];
bool row[N], col[N], dg[N], udg[N]; // 因为是一个个搜索，所以加了row

// s表示已经放上去的皇后个数
void dfs(int x, int y, int s)
{
    // 处理超出边界的情况
    if (y == n) y = 0, x ++ ;

    if (x == n) { // x==n说明已经枚举完n^2个位置了
        if (s == n) { // s==n说明成功放上去了n个皇后
            for (int i = 0; i < n; i ++ ) puts(g[i]);
            puts("");
        }
        return;
    }

    // 分支1：放皇后
    if (!row[x] && !col[y] && !dg[x + y] && !udg[x - y + n]) {
        g[x][y] = 'Q';
        row[x] = col[y] = dg[x + y] = udg[x - y + n] = true;
        dfs(x, y + 1, s + 1);
        row[x] = col[y] = dg[x + y] = udg[x - y + n] = false;
        g[x][y] = '.';
    }

    // 分支2：不放皇后
    dfs(x, y + 1, s);
}


int main() {
    cin >> n;
    for (int i = 0; i < n; i ++ )
        for (int j = 0; j < n; j ++ )
            g[i][j] = '.';

    dfs(0, 0, 0);

    return 0;
}