https://codeforces.com/contest/1607/problem/H
这道题的大意：给定n组数(a, b), m, 其中可以对a，b分别减去一定的数x, y满足x <= a, y <= b,
x + y = m, 得到点对(a - x, b - y)，求n组点对分别进行相减后最少有多少种不同的点对?
思考：
这道题是让我们把点对尽量变成相同的，那么能够使两（多）组点对通过减法操作使其相同的必要条件是(ai + bi - mi) = (aj + bj - mj) = c，所以我们首先对点对按照a + b - m的值进行分类然后放在不同的集合中，同一集合里的点对有可能会变得相同，而不同集合的点对相互之间是不可能变得相同的。所以我们只需要分别看每个集合，关注集合里的点对相互之间的关系就可以了，那么对于处于同一集合里的点对，想要使他们相同只需要满足进行减法操作时ai - xi = aj - xj即可，因为ai + bi - mi = aj + bj - mj，ai - xi相同以后，自然bi - yi也就相同了(xi + yi = m), 那么ai - xi是一个是什么样的数呢？由于0 <= xi <= min(ai, m)，
所以max(ai - m, 0) <= ai - xi <= ai，对于每一个点对，进行减法操作之后a值得范围是
[max(ai - m, 0), ai]，那么我们要使多组a相同，实际上就是在多个区间分别挑选一个点作为a的值，使得点的种类最少，那么这不就是区间选点问题吗？https://www.acwing.com/problem/content/907/
区间选点问题的描述是：
给定 N 个闭区间[ai,bi]，请你在数轴上选择尽量少的点，使得每个区间内至少包含一个选出的点。
输出选择的点的最小数量。
所以我们直接用贪心就可以算出选择最少的点
这里补充一下贪心的做法：
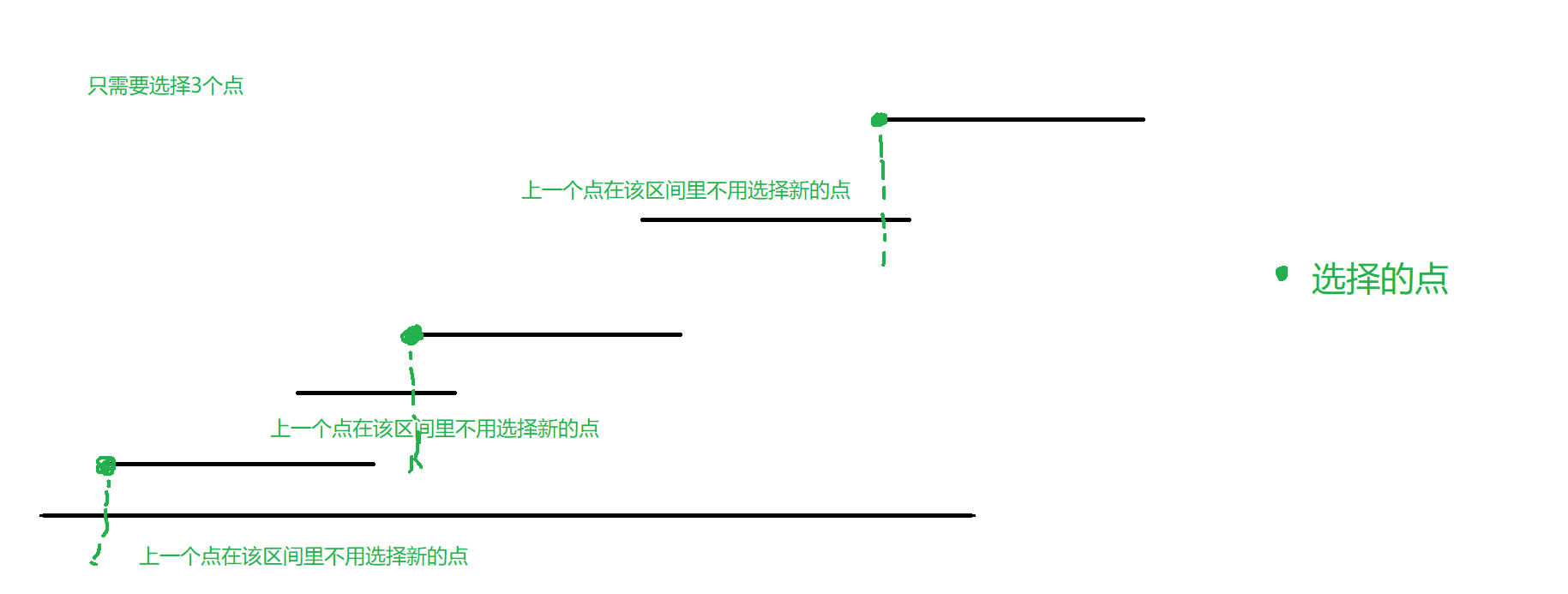
对所有区间按照左端点从小到大排序，然后从大往小遍历区间，如果上一次选的点还是在区间内部的话，就不用选新的点，否则选择该区间左端点（如图所示）

下面是代码：

#include <iostream> 
#include <algorithm> 
#include <cstring> 
using namespace std; 
const int N = 2e5 + 10; 
typedef pair<int, int> PII;
typedef pair<PII, int> PIII; // ((l, r), id)
#define x first
#define y second

struct Node {
    int a, b, m, id; 
    bool operator < (const Node& t) const {
        return a + b - m < t.a + t.b - t.m;  
    }
} q[N]; 

PIII p[N]; 
int tt;
int a[N], b[N], m[N], res_a[N]; // res_a[N]记录的是a剩下的值 

int main() { 
    int T, n; 
    cin >> T;
    while (T--) { 
        cin >> n;
        for (int i = 0; i < n; ++i) {
            cin >> a[i] >> b[i] >> m[i]; 
            q[i] = {a[i], b[i], m[i], i}; 
        }
        sort(q, q + n); 
        int j = 0, res = 0; 
        while (j < n) { 
            tt = 0;
            p[tt++] = {{max(q[j].a - q[j].m, 0), q[j].a}, q[j].id}; j++; 
            while (j < n && q[j].a + q[j].b - q[j].m == q[j-1].a + q[j-1].b - q[j-1].m) {
                p[tt++] = {{max(q[j].a - q[j].m, 0), q[j].a}, q[j].id};
                j++;    
            }
            // 区间选点 
            sort(p, p + tt);    
            int cur = 1e9; 
            for (int i = tt - 1; i >= 0; --i) {
                if (cur > p[i].x.y) {
                    cur = p[i].x.x;
                    res++;
                }
                res_a[p[i].y] = cur;    
            }
        }
        cout << res << endl; 
        for (int i = 0; i < n; ++i) 
            cout << a[i] - res_a[i] << ' ' << m[i] - (a[i] - res_a[i]) << endl; 
    }
    return 0;
}