dp
f[r][c][cut] 表示以(r,c)为左上角坐标有cut刀次数的切法数

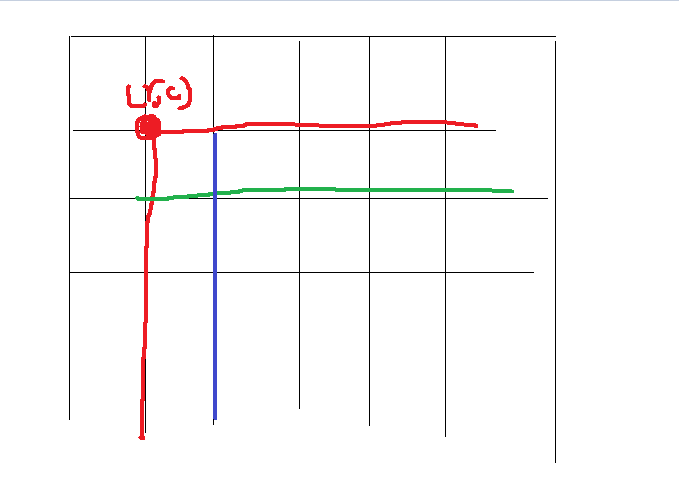
如图所示对于这个子问题，可以竖着切，也可以横着切:
f[r][c][cut] = sum(f[i][c][cut-1]) + sum(f[r][j][cut-1])

注意合法的切法切完，由于左半边和上半边根据规则被分发，因此必须满足hasapple(左半边/上半边)，

hasapple是我们定义的类似于前缀和的buffer，用来存储(i,j)点右下方的苹果数量，通过计算可以判断任意区域是否有苹果
复杂度为O(mnk),计算hasapp复杂度O(mn)

class Solution {
public:
    const int P=1e9+7;
    int ways(vector<string>& pizza, int k) {
        int m = pizza.size();
        int n = pizza[0].size();
        vector<vector<int>> hasapp(m+1, vector<int>(n+1,0));
        vector<vector<vector<int>>> f(m+1, vector<vector<int>>(n+1, vector<int>(k,0)));
        //hasapple
        for (int i = m-1;i>=0;i--){
            for (int j =n-1;j>=0;j--){
                hasapp[i][j] = hasapp[i+1][j] + hasapp[i][j+1] - hasapp[i+1][j+1] + (pizza[i][j] == 'A');
            }
        }
        for (int r=0;r<m;r++){
            for (int c=0;c<n;c++){
                if (hasapp[r][c]) f[r][c][0] = 1;
            }
        }
        for (int cut = 1;cut<k;cut++){
            for (int r = m-1;r>=0;r--){
                for (int c = n-1;c>=0;c--){
                    int sum = 0;
                    //horizonal
                    for (int i=r+1;i<m;i++){
                        if (hasapp[r][c] - hasapp[i][c]) sum =(sum+f[i][c][cut-1]) % P;
                    }
                    //vertical
                    for (int j=c+1;j<n;j++){
                        if (hasapp[r][c] - hasapp[r][j]) sum = (sum+f[r][j][cut-1]) % P;
                    }

                    f[r][c][cut] = sum;
                    // cout<<"r="<<r<<' '<<"c="<<c<<' '<<"cut="<<cut<<' '<<"f="<<sum<<endl;
                }
            }
        }

        return f[0][0][k-1];
    }
};