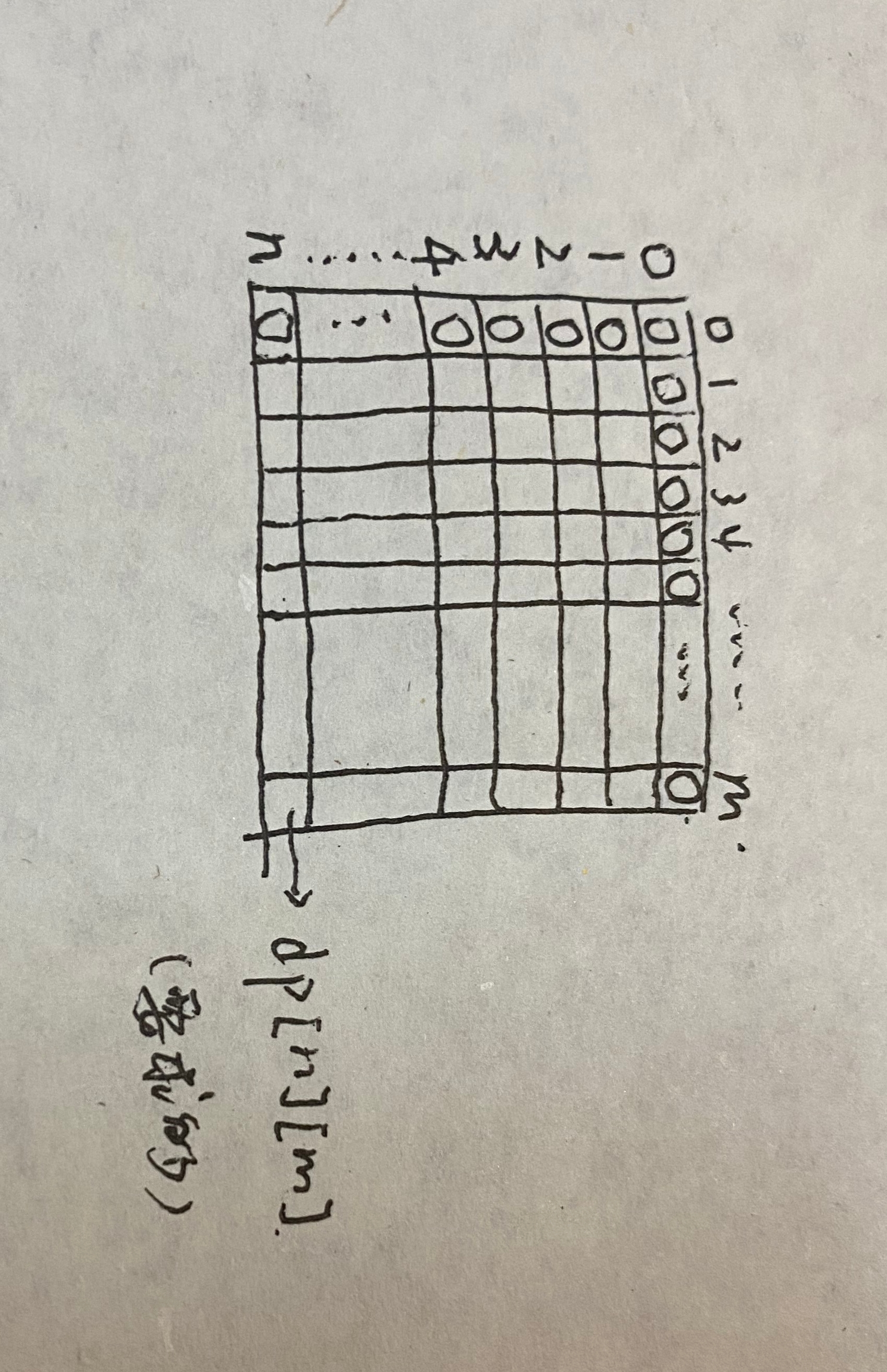
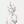动态规划问题其实就是拿状态转移方程去自底向上填表，以求得最顶层所要求的状态的过程
而0-1背包的优化（二维降一维）就是填表过程的一种优化，这种优化主要是空间上的优化，采取滚动数组的形式

由状态转移方程：dp(i,j)=max(dp(i-1,j),dp(i-1,j-v)+w),去填表的过程中我们发现，如计算dp(3,3)的时候只用到了dp(2,3)和与其同行前面的几个状态，
也就是我们在计算第i行的状态时只会用到上一行的状态，且都在我们要计算状态的同侧，这样我们用一维滚动数组，反复计算覆盖就可以完成。
我们要用一维数组实现多维数组同样的功能，就要保证，我们在计算第i层状态的时候，一维数组中必须完好保存着i-1层的状态
在顺序填写滚动数组的时候，出现了如下问题：

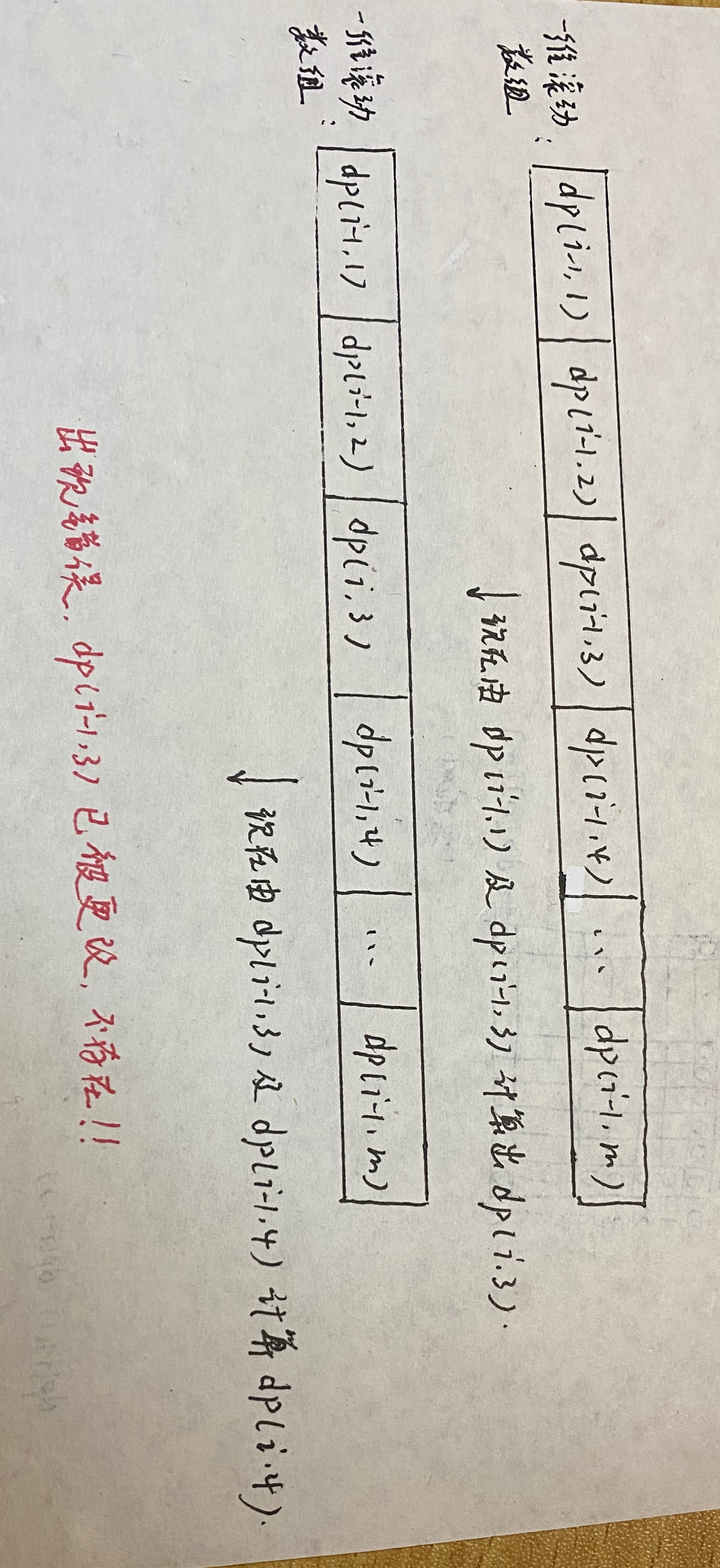
要解决如下问题，我们需要逆序（从后往前）填写滚动数组

具体代码实现，只需要去掉第一维,逆序循环就行了

#include<bits/stdc++.h>

using namespace std;

const int N=1010;

int n,m,v[N],w[N],dp[N];

int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>v[i]>>w[i];

    for(int i=1;i<=n;i++)
      for(int j=m;j>=1;j--)
      {
          if(j<v[i]) dp[j]=dp[j];
          else dp[j]=max(dp[j],dp[j-v[i]]+w[i]);
      }

    cout<<dp[m];

    return 0;
}

更优美一点写法：

#include<bits/stdc++.h>

using namespace std;

const int N=1010;

int n,m,v[N],w[N],dp[N];

int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>v[i]>>w[i];

    for(int i=1;i<=n;i++)
      for(int j=m;j>=v[i];j--)
         dp[j]=max(dp[j],dp[j-v[i]]+w[i]);

    cout<<dp[m];

    return 0;
}