正文篇
第二章 DFS 题目的状态空间与转换
$2.1$ DFS 在地图类问题的转换
* DFS 维护连通块
在一个平面的地图上,仅用 $x、y$ 这两个坐标就可以描述地图上任意一个点。
将 起点 看作 根, 起点可走到的格子 看作往外延伸的 子节点,在搜索过程中维护当前答案。
通常在每次递归时,我们会 新建一个变量(或在全局开一个数组)来累计答案。
但经过仔细分析之后,可以得出,这类问题的 搜索答案往往与路径相关,所以,可以用记忆化搜索解决。
下一步,就是如何处理状态。
下面这个程序所解决的题目,只需要知道 第$x, y$个格子是否被遍历过,由于此题的数据是一张图,所以不需要回溯。
只需要用一个数组的值就可以精准记录了。
int dfs(int x, int y)
{
int cnt = 1;
st[x][y] = true;
for (int i = 0; i < 4; i ++ )
{
int a = x + dx[i], b = y + dy[i];
if (a < 0 || a >= h || b < 0 || b >= w) continue;
if (g[a][b] != '.') continue;
if (st[a][b]) continue;
cnt += dfs(a, b); // 相加
}
return cnt;
}
* DFS 有约束的跑图问题
往往一道 $DFS$ 的题目会给你加上各式各样的约束,如何将这些约束合适的表达出来。
就是一门值得深究的学问了。
这是一道非常经典的题目,也是作者在 3个月前,初学 $DFS$ 的时候印象极为深刻的题目之一。
面对一道陌生的问题,我们需要对它进行合理的转化(至少在联赛难度的时候这个方法是适用的)
很明显,我们可以从图上任意一点出发,搜索可以滑的最大距离,维护最大值即可。
但这样的复杂度是 $O((nm)^2)$, 显然超时。
结合 池塘计数 一题, 我们知道,并不是每一次搜索的时候都要将所有点都搜一遍。
回到此题,由于每一个点的 最大滑行距离固定,而对任意一个点而言,其最大滑行距离等价于
他能滑到的点中滑行距离最大的点 加 $1$。
所以,我们可以用 $f$ 数组记忆化维护每个点的最大滑行距离,在搜到这个点时,直接返回 $f$ 中储存的数即可。
无疑,这是一道经典模型的加强,让我们先为它划定状态空间。
即对于此图上的任意一点都有 三个变量,它的 $x, y$ 坐标和它上一步的方向 $k$。
这三类变量都可以用一个 $f$ 的三维数组来储存,设 $a, b, p$ 意义分别对应上面的 $x, y, k$。
若 $f[a][b][p]$ 被更新过,有知,$f[a][b][p]$ 储存的是 $a, b$ 坐标,上一步为 $p$ 的最大值,所以不用继续搜。
同时,我们还不能 重复经过一个格子,所以,需要用 $st$ 来判断格子是否已经经过,
需要注意的是,$st$ 并不是记忆化搜索,因为 到达一个格子的状态可能有很多个,不能以一概全。
所以我们还要在 延伸后回溯。
值得注意的是,以上操作都是在默认从终点出发为前提的,那么,其递归边界就是 起点。
状态转移,由于数据的特殊,我们将数据 逆时针转 90度 来看,那么三个转移过程是:
0. 向左转移
LL Left(int x, int y)
{
int a, b;
LL ans = -INF;
a = x - 1;
b = y;
if (check(a, b) && !st[a][b])
{
LL res = max(dfs(a, b, 1) + g[x][y], dfs(a, b, 2) + g[x][y]);
ans = max(ans, res);
}
return ans;
}
1. 向上转移
LL Up(int x, int y)
{
int a, b;
LL ans = -INF;
a = x;
b = y - 1;
if (check(a, b) && !st[a][b])
{
LL res = max(max(dfs(a, b, 0) + g[x][y], dfs(a, b, 2) + g[x][y]), dfs(a, b, 1) + g[x][y]);
ans = max(ans, res);
}
return ans;
}
2. 向右转移
LL Right(int x, int y)
{
int a, b;
LL ans = -INF;
a = x + 1;
b = y;
if (check(a, b) && !st[a][b])
{
LL res = max(dfs(a, b, 1) + g[x][y], dfs(a, b, 0) + g[x][y]);
ans = max(ans, res);
}
return ans;
}
递归代码:
inline bool check(int x, int y)
{
return x >= 1 && x <= n && y >= 1 && y <= m;
}
inline LL dfs(int x, int y, int k)
{
LL &ans = f[x][y][k];
if (ans != -INF)
{
return ans;
}
st[x][y] = true;
if (k == 0) ans = max(ans, Right(x, y));
if (k == 1) ans = max(ans, Up(x, y));
if (k == 2) ans = max(ans, Left(x, y));
st[x][y] = false;
return ans;
}
* DFS 解决棋盘类问题
我们在研究深搜算法时经常能碰到这一类问题:
在某个棋盘上有一种棋子,问最多放下几个棋子,使得剩下来的棋子两两不攻击。
这就是 棋盘类问题。
或者,也可以广义的理解为,在一张图上放上一些满足一定规律的点,让你输出其中的 放点方案 或者是 方案数。
常考题型有 八皇后问题、数独问题、多米诺骨牌(块状覆盖问题)。
下面我会教大家解决这些问题的变种,难度按递增顺序排列。
这是一道经典问题的变形,同样也是方案数类问题的基础题,看似简单,却往往能将你折磨得怀疑人生。
让我们从头分析吧!
首先,确定搜索方式,显然是一个排列型枚举。
但如果这样,它的时间复杂度会飙升到 $64!$, 不能接受,所以,我们需要根据题意进行简化。
通常,可以用两个数组来记录 这一行或者这一列 是否有了棋子。
或者,也可以直接 按行枚举,提升效率。
然后,就要确定搜索边界,通常有两个:越出边界 和 枚举完所有数字。
其实,还是挺简单的,那就稍微加深点难度吧!
非常经典的问题,也是一道用来练习码力的入门题,在做完猪国杀之前,一度是我调试代码的噩梦。
这道问题涉及的内容很多,如果你不知道怎么剪枝来提升效率,可以先学习一下我之后分享的内容。
话不多说,让我们先来看一下搜索方式,显然,每个位置都有很多种填数的方案,是 排列型枚举
在想一下有哪些需维护的信息,例如,枚举的空格数便是其中之一,注意只有没有数字的格子才能去填。
数独问题是一道典型的 $NPC$ 问题,我们需要进行回溯,通常使用二进制 $hash$表的方式来储存数独问题的状态。
边界就很显然了,在它的所有空格都正确填完之后,返回输出即可,一般是保证了唯一解的。
如果你觉得简单的话,也可以试一下这道题,无疑是对自己程序设计的一个挑战。
让我们来看一道算法竞赛题真正的难度吧!
即使是身经百战的老手也很难快速解决这种问题,但也是你迈向更高道路上必经之路。
$2.2$ DFS 搜索最优解
这一类问题需要你在搜索的过程中,保留局部最优方案,排除大于局部最优的方案,进而得出全局最优解。
下面会介绍解决这一类问题的两种方案。
1. 贪心法
将答案进行比对,保留自己需要的哪个答案,就是贪心法。
由于车和每辆缆车中装载的小猫状态并未固定,也就是说,我们需要用两个状态来表示。
状态转移途径有两条,一、装这个小猫到这个车,二、增加或不增加车
此状态边界无疑就是装完所有小猫的时候,但装完小猫的情况有很多,我们要取的就是用车数最小的一种。
2. 迭代法 / 二分法
适用于答案可能性较少或边界模糊的题目,可以规定边界,转化为满足性问题。
这道题要求的是木棒的可能最小长度。
由于木棒的总长度固定,所以可以转换为枚举目标木棍长度(显然是整除总长度的)。
由于已拼好的木棒不用重拼,所以可以将边界设为已拼好木棒总长度 = 木棒总长度,
由于木棒的拼接是有序的,也可以说是一个 $DFS$ 的基本拼凑类题目。
由此推出木棒数量和当前所拼木棒长度可以设为变量。
这道题的剪枝就不设为本章讲解内容了。
$2.3$ DFS 搜索最优方案路径
这是一个适用性很广的算法,体现了路径追踪的思想。
当然,你必须要保留之前递归时状态转移的过程。
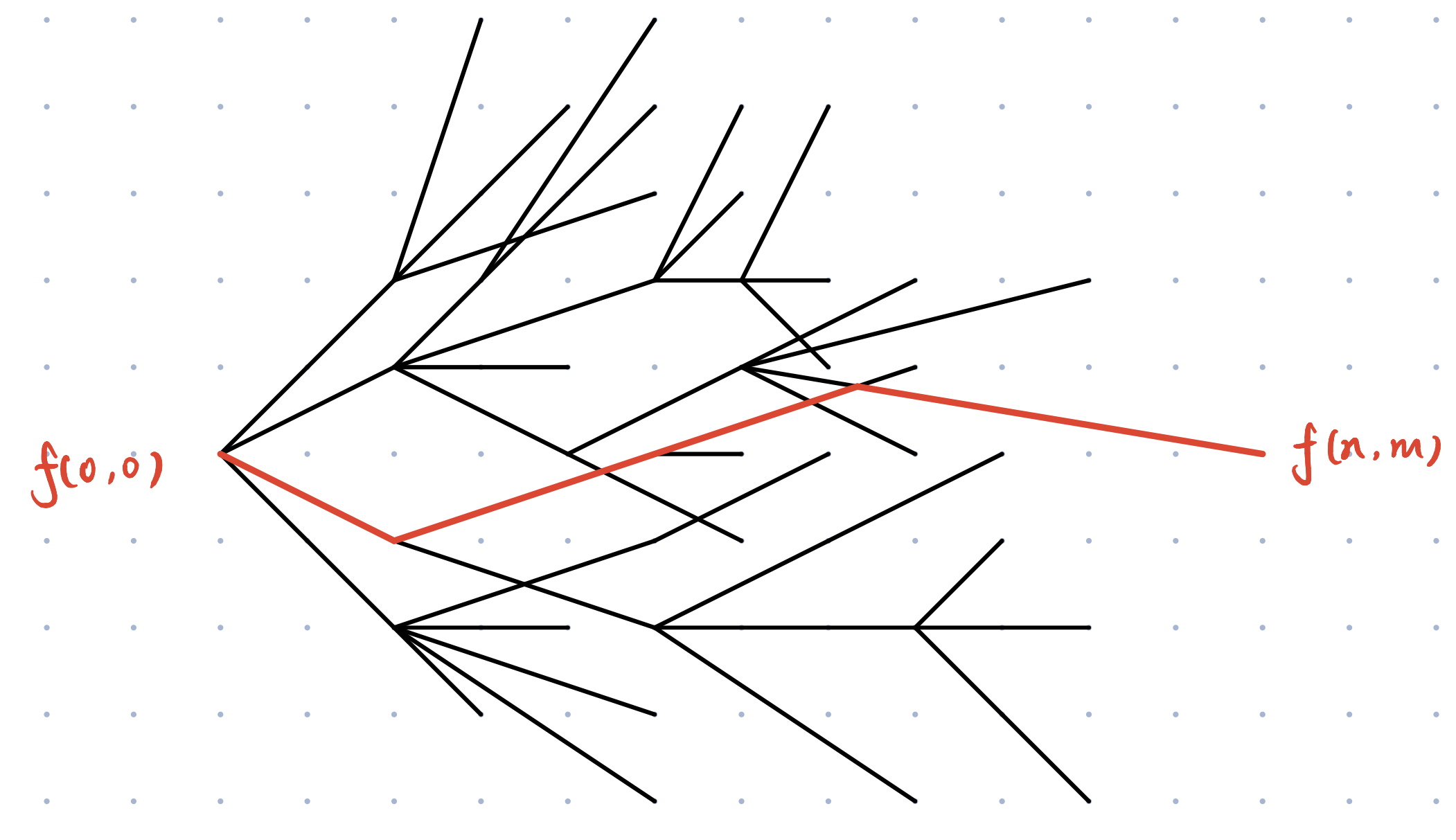
上面这个图是彩铅的。
其解决方式为,由答案逆推,枚举上一层可到达答案的状态,继续逆推至起点。
$2.4$ DFS 搜索方案数
乍一看,这是一个很令人难受的问题QAQ,但事实并非如此,
若将初始状态看成起点,答案看成终点,本问可以转化为,从起点可以到达终点的路径有多少条。
在每一次递归到答案时统计就可以了。

