1、二进制矩阵

原题

变化过程

通过三次变化后，只把1变为0，其他位置的数不改变

#include <iostream>
using namespace std;
const int N = 110;

int n, m;
char g[N][N];

void print() {
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            cout << g[i][j] << ' ';
        }
        cout << endl;
    }
    cout << endl;
}

void printL(int i, int j, int k) {
    // k 顺时针
    if (k == 0) {
        printf("%d %d %d %d %d %d\n", i, j, i + 1, j, i, j + 1);
    } else if (k == 1) {
        printf("%d %d %d %d %d %d\n", i, j - 1, i, j, i + 1, j);
    } else if (k == 2) {
        printf("%d %d %d %d %d %d\n", i - 1, j, i, j, i, j - 1);
    } else {
        printf("%d %d %d %d %d %d\n", i - 1, j, i, j, i, j + 1);
    }
}

int main() {
    int T;
    cin >> T;
    while (T--) {
        cin >> n >> m;
        int res = 0;
        for (int i = 1; i <= n; i++) {
            cin >> g[i] + 1;
            for (int j = 1; j <= m; j++) {
                if (g[i][j] == '1') {
                    res += 3;
                }
            }
        }
        print();
        cout << res << endl;
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                if (g[i][j] == '1') {
                    if (i < n && j < m) {
                        // 0
                        printL(i, j, 0);
                        printL(i, j + 1, 1);
                        printL(i + 1, j, 3);
                    } else if (i == n && j == m) {
                        // 2
                        printL(i, j, 2);
                        printL(i - 1, j, 1);
                        printL(i, j - 1, 3);
                    } else if (i == n) {
                        // 3
                        printL(i, j, 3);
                        printL(i - 1, j, 0);
                        printL(i, j + 1, 2);
                    } else {
                        // 1
                        printL(i, j, 1);
                        printL(i, j - 1, 0);
                        printL(i + 1, j, 2);
                    }
                }
            }
        }
    }
    return 0;
}


/*

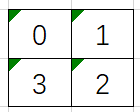
k:
0 1
3 2

*/

2、数字矩阵

原题

思路

依据：通过操作，矩阵中任意位置两个元素能同时变号
统计矩阵中，负数的个数：
1.负数个数为奇数，能变成只有一个负数，选择这个数是绝对值最小的即可
2.负数个数为偶数，能同时都变成正数

#include <iostream>
using namespace std;

int n, m, T, a;
int abs(int x) {
    return x >= 0 ? x : -x;
}

int main() {
    cin >> T;
    while (T--) {
        cin >> n >> m;
        int oddNum = 0, sum = 0, x = 1e9;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                cin >> a;
                if (a < 0) {
                    oddNum++;
                }
                if (abs(a) < x) {
                    x = abs(a);
                }
                sum += abs(a);
            }
        }
        if (oddNum % 2 == 1) {
            sum = sum - 2 * x;
        }
        cout << sum << endl;
    }
    return 0;
}