2.11 哈希表

• 存储方式
• 开放寻址法
• 拉链法
• 字符串哈希方式

哈希函数

• 直接取模(取模时一般要取质数，要离2的整数次幂尽可能地远，这样取冲突概率最小)
• 解决冲突两种方式

拉链法

//找质数
#include<iostream>

using namespace std;

int main(){
    int i;
    for(i = 100000;; i ++ ){
        bool flag = true;
        for(int j = 2; j * j <= i; j ++ ){
            if(i % j == 0){
                flag = false;
                break;
            }
        }
        if(flag) {
            cout << i << endl;
            break;
        }
    }

}

const int N = 100003;

int h[N], e[N], ne[N], idx;

void insert(int x){
    int k = (x % N + N) % N;
    e[idx] = x;
    ne[idx] = h[k];
    h[k] = idx ++;
}

bool find(int x){
    int k = (x % N + N) % N;
    for(int i = h[k]; i != -1; i = ne[i])
        if(e[i] == x)
            return true;
    return false;   
}

开放寻址法

• 如何处理冲突 ：找坑位，如果该坑位有人则去下一个坑位找。

• 只开一个数组，防止坑位满一般要开原大小的2~3倍

• 如果操作数量N = 100000,先找一个大于二十万的最小的质数

• 核心操作： 如果x再哈希表中，k就是x的下标，如果不在哈希表中，k就是x应该存储的位置

代码

const int N = 200003, null = 0x3f3f3f3f;
/*
我们常采用0x3f3f3f3f来作为无穷大。0x3f3f3f3f主要有如下好处：
0x3f3f3f3f的十进制为1061109567，和INT_MAX一个数量级，即10^9数量级，而一般场合下的数据都是小于10^9的。
0x3f3f3f3f * 2 = 2122219134，无穷大相加依然不会溢出。
可以使用memset(array, 0x3f, sizeof(array))来为数组设初值为0x3f3f3f3f，因为这个数的每个字节都是0x3f。-----来源于评论
*/

int h[N];

int find(int x){
    int k = (x % N + N) % N;

    while(h[k] != null && h[k] != x){
        k ++;
        if(k == N) k = 0;
    }

    return k;//如果x在哈希表中，k就是x的下标，如果不在哈希表中，k就是x应在存储的位置
}

int main(){
    int n;
    scanf("%d", &n);

    memset(h, 0x3f, sizeof h);//按字节来的，h是int型，四个字节，每个字节3f

    while(n --){
        char op[2];
        int x;
        scanf("%s%d", op, &x);

        int k = find(x);
        if(*op == 'I') h[k] = x;
        else{
            if(h[k] != null) puts("Yes");
            else puts("No");
        }
    }
}

字符串哈希

好处：算出任意一个子串的hash

已知

• 一个字符串”ABCABCDEYXCACwing“
• 问某两个区间所包含的字符串是否完全相同

字符串前缀哈希法基本步骤

1. 用h[i]数组表示前i个字符串的hash值

2. h[0] = 0, h[1] = “A”的hash， h[2] = “AB”的hash......h[n]=前n个字符的hash

3. 比较这个字符串的某两个字串就是比较这两个字串的hash值。

4. 怎么将前缀字符串的hash值映射出来呢

5. 我们知道每个字符都有不同的ASCII码，我们把每个字符串看成P进制的数,那样的话不同的字符串就对应不同的hash值

6. $X1X2X3⋯Xn−1Xn$ 的字符串映射公式$ (X1×P^n−1+X2×P^n−2+⋯+Xn−1×P^1+Xn×P^0)modQ$

7. 我们就能求出任意字符串的hash值——
   

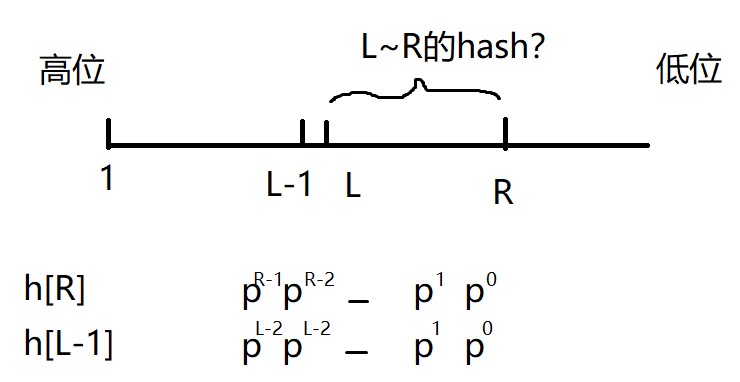
$h[L,R] = h[R] - h[L-1]×P^{R-L+1}$(让h[L-1]左移，使得h[R]和h[L-1]对齐)

注意

1. $P$, $Q$均为经验值，$P$一般取131或13331， $Q$一般取$2^{64}$
2. 每个字符都不能映射成0，否则有相同字符的的字符串就都是0，会产生冲突
3. 每个字符串类似于二进制，左边是高位，右边是低位

#include<iostream>

using namespace std;

const int N = 100010, P = 131;
typedef unsigned long long ULL;
ULL h[N], p[N];

ULL query(int l, int r){
    return h[r] - h[l - 1] * p[r - l + 1];
}

int main(){
    string s;
    int n, m;
    scanf("%d%d%s", &n, &m, s.c_str());
    p[0] = 1, h[0] = 0;
    for(int i = 0; i < n; i ++ ){
        p[i + 1] = p[i] * P;
        h[i + 1] = h[i] * P + s[i]; 
    }

    while(m --){
        int l1, r1, l2, r2;
        scanf("%d%d%d%d", &l1, &r1, &l2, &r2);
        if(query(l1, r1) == query(l2, r2)) puts("Yes");
        else puts("No");
    }

    return 0;
}