多边形283 yz视频清清楚楚

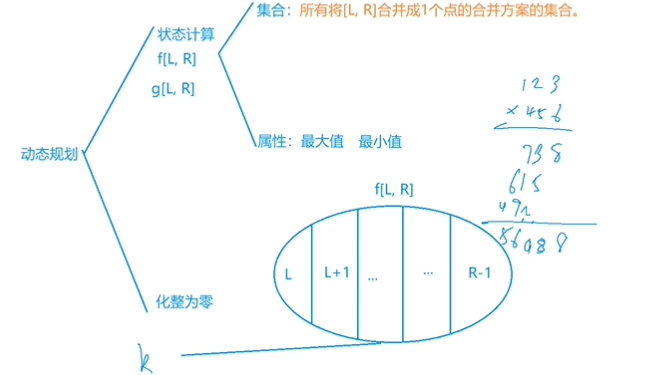
//要求环上的最优解时，先断开转化成链上的问题 从环上断开总共n种方式 长度总是为n的区间
//给定2n区间，把其中连续的n个数合并成一个数，所有这样的合并方式里面最大值是多少
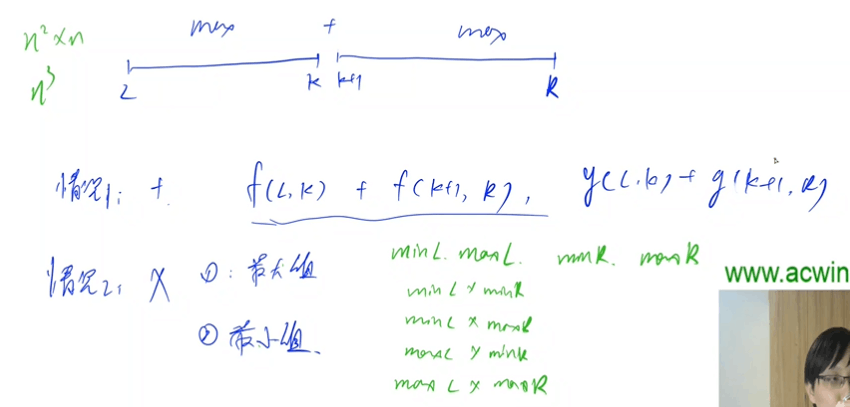
//破坏成链 最后是把两部分合并 左边部分最大是R-1
//情况1 +:f[l,k]+f[k+1,r]
//情况2 *:记录最大值同时记录最小值 总共九种情况四种结果 对于maxL,minL,maxR,maxR四种直接相乘无脑求最大和最小
#include<bits/stdc++.h>
using namespace std;
int n;
const int N=110,INF=32768;//环是两倍长
char c[N]; 
int w[N];
int f[N][N],g[N][N];

int main(){
    cin>>n;
    for(int i=1;i<=n;i++){//输入 把环变链
        cin>>c[i]>>w[i];
        c[i+n]=c[i];
        w[i+n]=w[i];
    }
    //以长度为大循环  枚举每个切断点   长度总是为n的区间
    for(int len=1;len<=n;len++)
    {
        for(int l=1;l+len-1<=2*n;l++)
        {
            int r=l+len-1;
            if(len==1) f[l][r]=g[l][r]=w[l];//l，r这里相等
            else
            {
                f[l][r]=-INF,g[l][r]=INF;//最大值正无穷，最小值负无穷
                for(int k=l;k<r;k++)
                {//枚举左边最后一个数
                    char op=c[k+1];   //编号从1开始
                    int minl=g[l][k],maxl=f[l][k],minr=g[k+1][r],maxr=f[k+1][r];
                    if(op=='t')
                    {
                        f[l][r]=max(f[l][r],maxl+maxr);
                        g[l][r]=min(g[l][r],minl+minr);
                    }
                    else
                    {
                        int x1=minl*minr,x2=maxl*minr,x3=maxl*maxr,x4=minl*maxr;
                        f[l][r]=max(f[l][r],max(max(x1,x2),max(x3,x4)));
                        g[l][r]=min(g[l][r],min(min(x1,x2),min(x3,x4)));
                    }
                }
            }
        }
    }
    int res=-INF;
    for(int i=1;i<=n;i++)res=max(res,f[i][i+n-1]);
    cout<<res<<endl;

    for(int i=1;i<=n;i++){
        if(res==f[i][i+n-1])cout<<i<<' ';
    }
    return 0;
}