A-Duplicate Strings

签到题，注意注意k也要开ll

#include<bits/stdc++.h>

using namespace std;
typedef long long ll;
int n,q;
string a;
ll sum[30];
const int mod=1e9+7;

int main()
{
    cin>>n>>q;
    cin>>a;
    for(int i=0;i<n;i++)
    {
        int d=a[i]-'a';
        sum[d]++;
    }
    ll res=1;
    while(q--)
    {
        int t;
        cin>>t;
        if(t==1)
        {
            ll k;
            cin>>k;
            res=res*(k+1)%mod;
        }
        else
        {
            char x;
            cin>>x;
            int b=x-'a';
            cout<<(sum[b]*res)%mod<<endl;
        }
    }
    return 0;
}

B-Non-interger Area

题意：给出n个点，任选三个点，使这三个点围成的三角形面积不是整数的方案数

每个点的坐标都可以分成奇奇 偶偶 奇偶 偶奇 四种 、
根据三角形面积公式 S==(x1(y2-y3)+x2(y3-y1)+x3*(y1-y2))/2 可得两种思路

思路1（范老师想到的）

对于四种坐标任选三种都是可以的，因此我们记录每种坐标的数量，直接输出即可

#include<bits/stdc++.h>

using namespace std;
#define x first
#define y second

typedef long long ll;

int main()
{
    int n;
    cin>>n;
    ll sum1=0,sum2=0,sum3=0,sum4=0;
    for(int i=0;i<n;i++)
    {
        ll x,y;
        cin>>x>>y;
        if(x%2&&y%2)
        sum3++;
        else if(x%2==0&&y%2==0)
        sum4++;
        else if(x&1)
        sum1++;
        else 
        sum2++;
    }
    cout<<sum1*sum2*sum3+sum1*sum3*sum4+sum2*sum3*sum4+sum1*sum2*sum4<<endl;
    //   123             134             234          124

    return 0;
}

思路2

根据面积公式，枚举三个点坐标的奇偶，若面积是奇数，答案++
最后算出的结果一定是重复的，根据样例2可知重复了6倍(菜鸡不清楚为啥)

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll ans=0,cnt[2][2];
int n;
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        ll x,y;
        cin>>x>>y;
        cnt[(x%2+2)%2][(y%2+2)%2]++;
    }
    for(int i=0;i<2;i++)
    {
        for(int j=0;j<2;j++)
        {
            for(int k=0;k<2;k++)
            {
                for(int l=0;l<2;l++)
                {
                    for(int p=0;p<2;p++)
                    {
                        for(int q=0;q<2;q++)
                        {
                            int u=(k-i)*(q-j)-(l-j)*(p-i);
                            if(u%2)
                            {
                                ans+=cnt[i][j]*cnt[k][l]*cnt[p][q];
                            }
                        }
                    }
                }
            }
        }
    }
    cout<<ans/6;
}

C-Division

题意：给定一个长度为n的数组以及k 每次选择一个长度>=k的区间，让区间内每个数/2.问是否能把数组全变成1

思路：我们对数组每个元素取log原问题就变成能否把数组都变成0，区间操作很容易想到差分，构造出差分数组，问题变成能否把差分数组全变成0
我们从前往后便利差分数组，用一个栈存差分数组元素>0且与现在位置距离>=k的下标，若遍历到差分数组元素<0且栈为空时无解，否则进行一次操作。
注意需要遍历到n+m，若只遍历到n，数组n-m+1----n位置的差分数组元素>0的地方无法入栈

#include<bits/stdc++.h>

using namespace std;
#define x first
#define y second

typedef long long ll;
typedef pair<int,int> pii;

const int N = 2e4+5;

int b[20005];
struct node{
    int l,r;
}ans[1000005];

int n,k;
stack<int> s;

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    int _;
    cin>>_;
    while(_--)
    {
        while(s.size())
        s.pop();
        int cnt=0;
        memset(b,0,sizeof b);

        cin>>n>>k;
        for(int i=1;i<=n;i++)
        {
            ll x;
            cin>>x;
          // while(x>1)x>>=1,b[i]++;
             while(x>1)
             b[i]++,x/=2;
        }
        //把原数组都变成1 相当于把b数组变为0
        //构造b的差分数组
        //对b 1--n操作相当于对c  1--n+1操作
        for(int i=n+1;i>=1;i--)
        {
            b[i]=b[i]-b[i-1];
        }

        int flag=1;
        for(int i=1;i<=n+k;i++)//要循环到n+m，因为要把后半段>0的部分入栈
        {
            if(i-k>=1)
            {
                 //assert(b[i-k]>=0);
                while(b[i-k]) s.push(i-k),b[i-k]--;
            }
            if(b[i]<0)
            {
                while(b[i])
                {
                        if(!s.size())
                    {
                        flag=0;
                        break;
                    }
                    b[i]++;
                    //cout<<"---"<<s.top()<<' '<<i-1<<endl;
                    ans[++cnt]={s.top(),i-1};
                    s.pop();
                }
            }
            if(!flag) break;
        }
        if(s.size()) flag=0;
        if(!flag)
        cout<<-1<<endl;
        else{
            cout<<cnt<<endl;
            for(int i=1;i<=cnt;i++)
            {

                cout<<ans[i].l<<' '<<ans[i].r<<endl;

            }

        }
    }

    return 0;
}

D-gcd

题意：一个长为n的数组，给出a[i]位于l[i]–r[i]之间，对于a[i]的所有情况gcd(a1,a2—an)的约数个数和

整除分块： https://www.cnblogs.com/peng-ym/p/8661118.html

思路：已知区间1-y中 x的倍数有y/x个，
对于本题枚举约数那问题就变成了
其中i是枚举的gcd的约束，但这样复杂度是3e5*1e5会t
已知整除分块是sqrt（n）的,某一个区间内的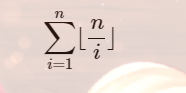相等那么本题的（r/i-(l-1)/i）也会存在某一个区间相等 ,那我们就可以进行一个差分
另val=（r/i-(l-1)/i）
对一个初始为1的差分数组（代表约数）每次进行区间乘法（val相等）的区间，若val为0可在用一个差分数组标记
答案就是差分数组的原数组的和

#include<bits/stdc++.h>

using namespace std;

#define x first
#define y second

const long long mod=998244353;
const int N = 1e5+10,M=3e5+20;;
typedef pair<int,int> pii;
typedef long long ll;

ll qmi(ll a,ll b)
{
    ll res=1;
    while(b)
    {
        if(b&1)
        res=res*a%mod;
        a=a*a%mod;
        b>>=1;
    }
    return res;
}

int n;
ll c[M];//区间乘法的差分数组
ll  b[M];//判断有无区间乘0操作
ll inv[M];//逆元数组

int main()
{
    for(int i=0;i<=300001;i++)
    c[i]=1;
    inv[1]=1;
    for(int i=2;i<=300001;i++)
    inv[i]=qmi(i,mod-2);
    cin>>n;
    int x,y;
    for(int i=1;i<=n;i++)
    {
        cin>>x>>y;
        x--;
        int l,r;
        for(int l=1;l<=y;l=r+1)//枚举约束
        {
            r=y / (y / l);//最后一个点
            if(l <= x)
            r=min(r,x / (x / l));
            int val=y/l-x/l;
            if(val)
            c[l]=c[l]*val%mod,c[r+1]=c[r+1]*inv[val]%mod;
            else
            b[l]++,b[r+1]--;
        }
        //约束应小于y
        b[y+1]++;
    }
    ll ans=0;

    for( int i = 1; i <= 300000; ++i )
    c[ i ] = c[ i ] * c[ i - 1 ] % mod;
    for( int i = 1; i <= 300000; ++i ) {

        b[ i ] += b[ i - 1 ];
        if( b[ i ] ) c[ i ] = 0;
    }

    for(int i=1;i<=300000;i++)
    {
       // if(!b[i])
        ans=(ans+c[i])%mod;
    }
    cout<<ans;
    return 0;
}