传纸条275 yzvideoyyds
四种状态转移过来见 官方题解

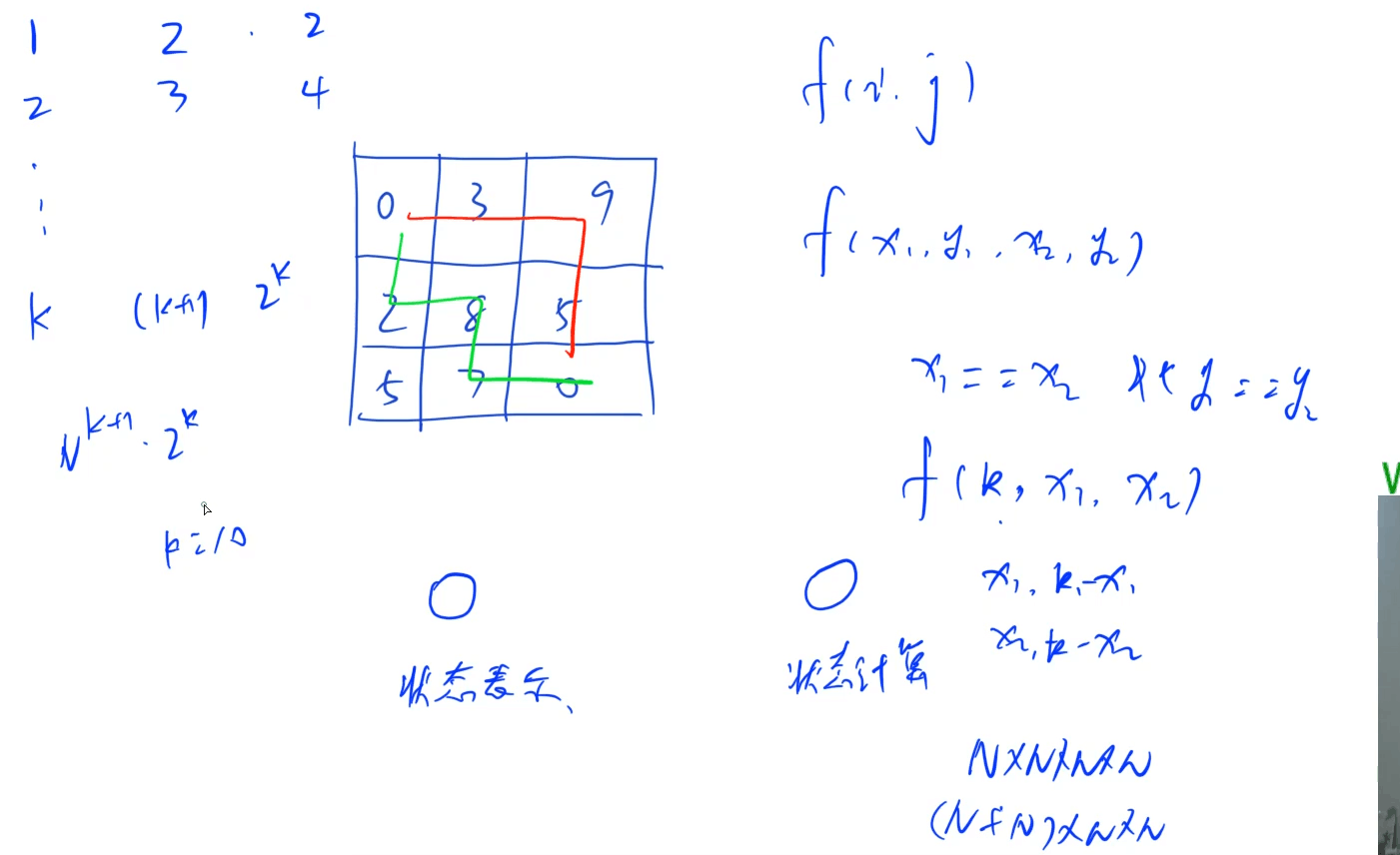
/*只走一次 所有从左上走到当前格子i，j的方案f(i,j)
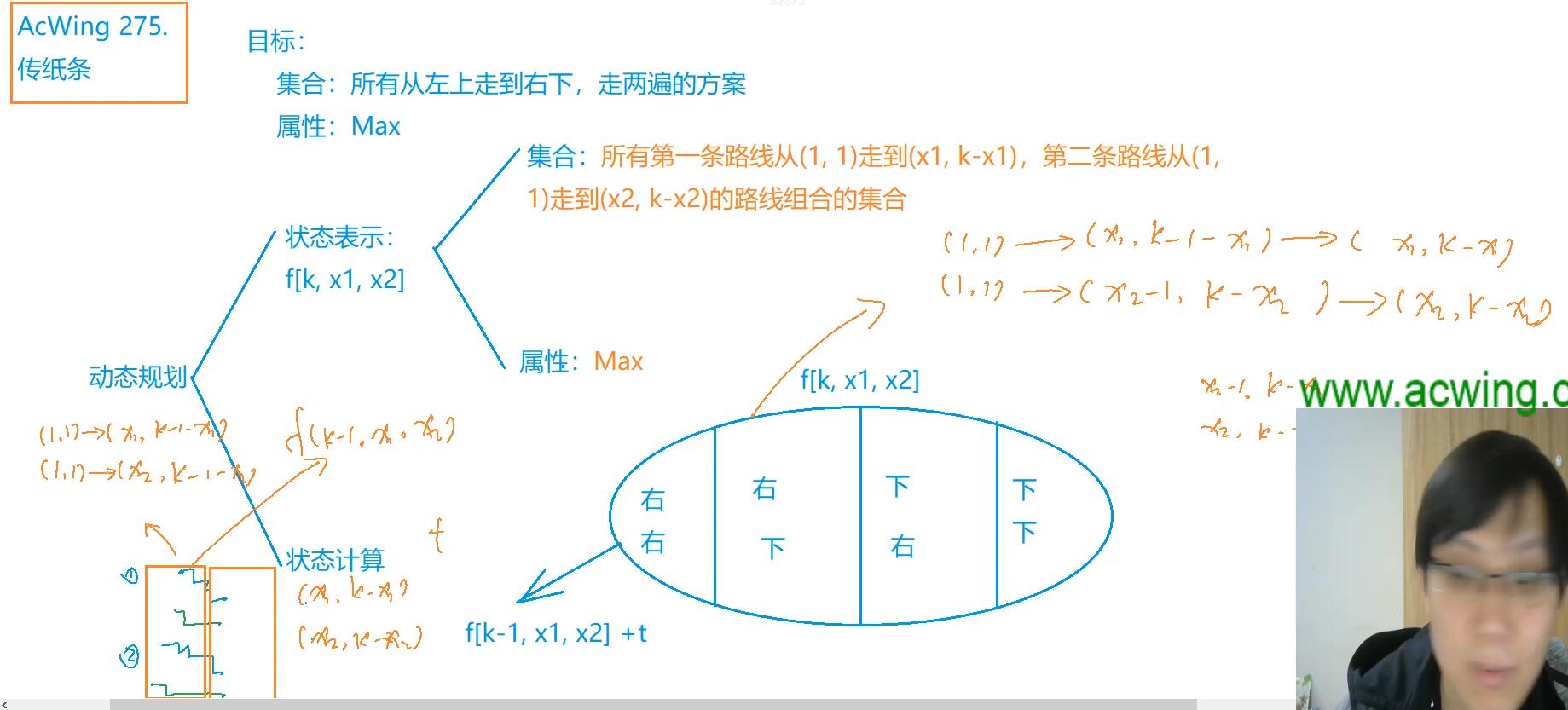
f(x1,y1,x2,y2)所有从左上，第一条走到x1,y1,第二条走到x2,y2的方案  
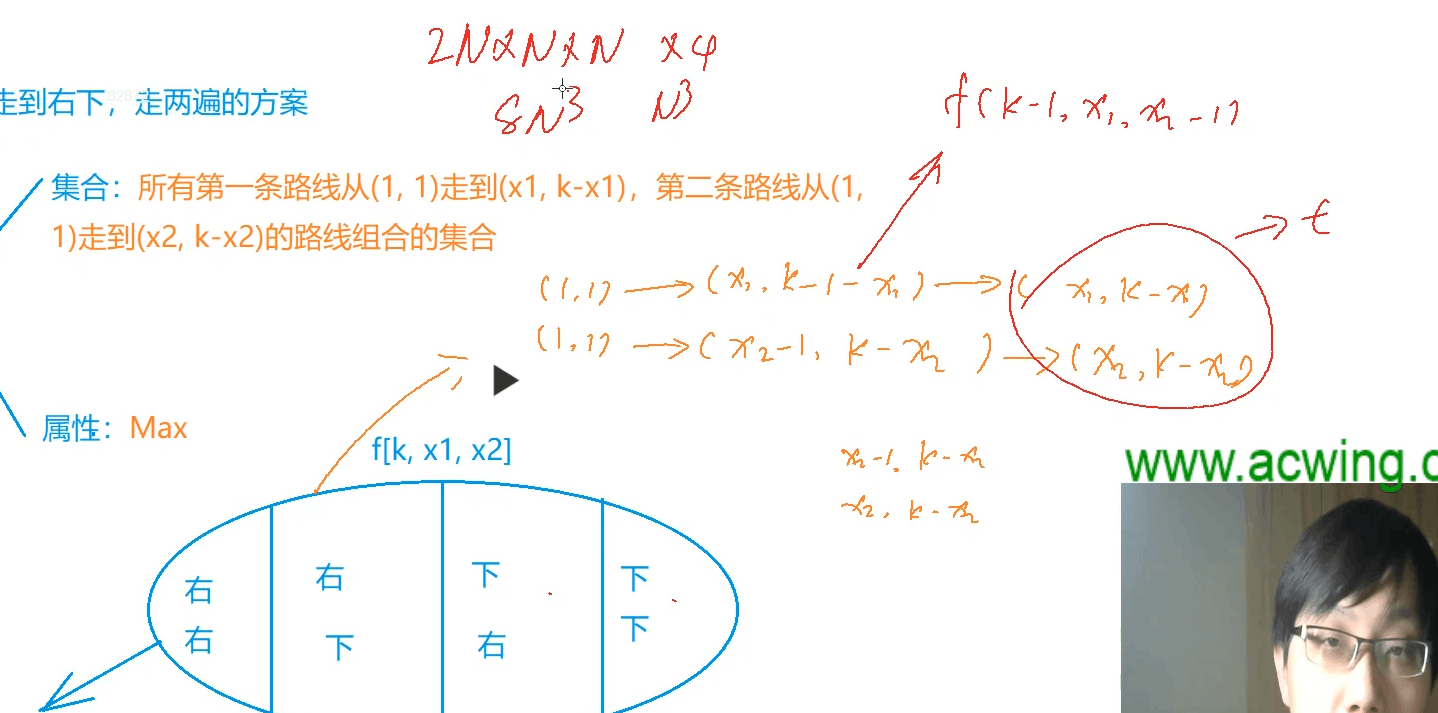
f(k,x1,x2)k表示两条路线的横纵坐标之和 坐标就是(x1,k-x1) (x2,k-x2) 只要能重合横坐标一样 
原来N^4 现在(N+N)*N*N  用x1==x2&&y1==y2来判断两种方案是否重合  
1路径用两维决策两个状态（2个路径取最大值） k=2三维四个状态取最大值  
k条路径（k+1）维2^k条路线的组合取最大值  N^(K+1)*2^K
K>=10这题用最小费用流来做
*/
#include <bits/stdc++.h>
using namespace std;

const int N = 55;

int n, m;
int g[N][N];
int f[N * 2][N][N];

int main()
{
    cin>>n>>m;
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            cin>>g[i][j];

    //1<=x1<=n&&1<=k-x1<=m    ==>  max(1,k-m)<=x1,x2<=min(k-1,n)
    for (int k = 2; k <= n + m; k ++ )
        for (int i = max(1, k - m); i <= n && i < k; i ++ )
            for (int j = max(1, k - m); j <= n && j < k; j ++ )
                for (int a = 0; a <= 1; a ++ )//可能存在有i-a == j-b的情况，这种情况f一定为0，所以不会是max
                    for (int b = 0; b <= 1; b ++ )
                    {
                        int t = g[i][k - i];
                        if (i != j || k == 2 || k == n + m)
                        {
                            t += g[j][k - j];   //两种路线没有重复
                            f[k][i][j] = max(f[k][i][j], f[k - 1][i - a][j - b] + t);
                            //当前状态可以从四种状态转移过来，同时那四种状态的i+j一定小于k，所以一定被遍历过
                        }
                    }

    cout<<f[n + m][n][n]<<endl;

    return 0;
}