题号68：查找漏的元素//

if(r<0)return 0;
while(l<r)
{
int mid=(l+r)>>1;
if(nums[mid]>mid)r=mid;//nums[mid]不可能小于mid,所以另一种情况就是nums[mid]==mid
else l=mid+1;          //所以这题二分的条件还可以是nums[mid]!=mid;
}
if(nums[r]==r)return r+1;
return r;

题目：14   不改变数组查找重复的元素要o（1）的空间（即不用hash表）那用二分

int cnt=0；
int mid=(l+r)>>1;
int i=0;
for(auto x:nums)cnt+=x<=mid&&x>=l;
if(cnt>mid-l+1)r=mid;
else l=mid+1;
return r;

而最佳牛围栏那道题二分的是这个数（mid）作为最优解可不可以，而不是对数组二分，二分的实质是分界性。

double l=1;
double r=1e5
while(r-l>1e-5)//因为要取到答案要求保留的位数的再后两位
{double mid=(l+r)/2;//因为不是int型所以不能用>>1;
if(check(mid))r=mid;
else l=mid+1;
}
//然后就是写最重要的check函数了
double check(double mid)
{for(int i=1;i<=n;i++)
{
    sum[i]=sum[i-1]+(cow[i]-mid);
}
double minnum=0;
for(int i=0,j=k;j<=n;i++,j++)//这样就满足了j与minnum代表的长度的差值一定大于等于k
    {minnum={minnum,sum[i]};
    if(sum[j]-minum>=0)return true;
    }
    return false ;
}

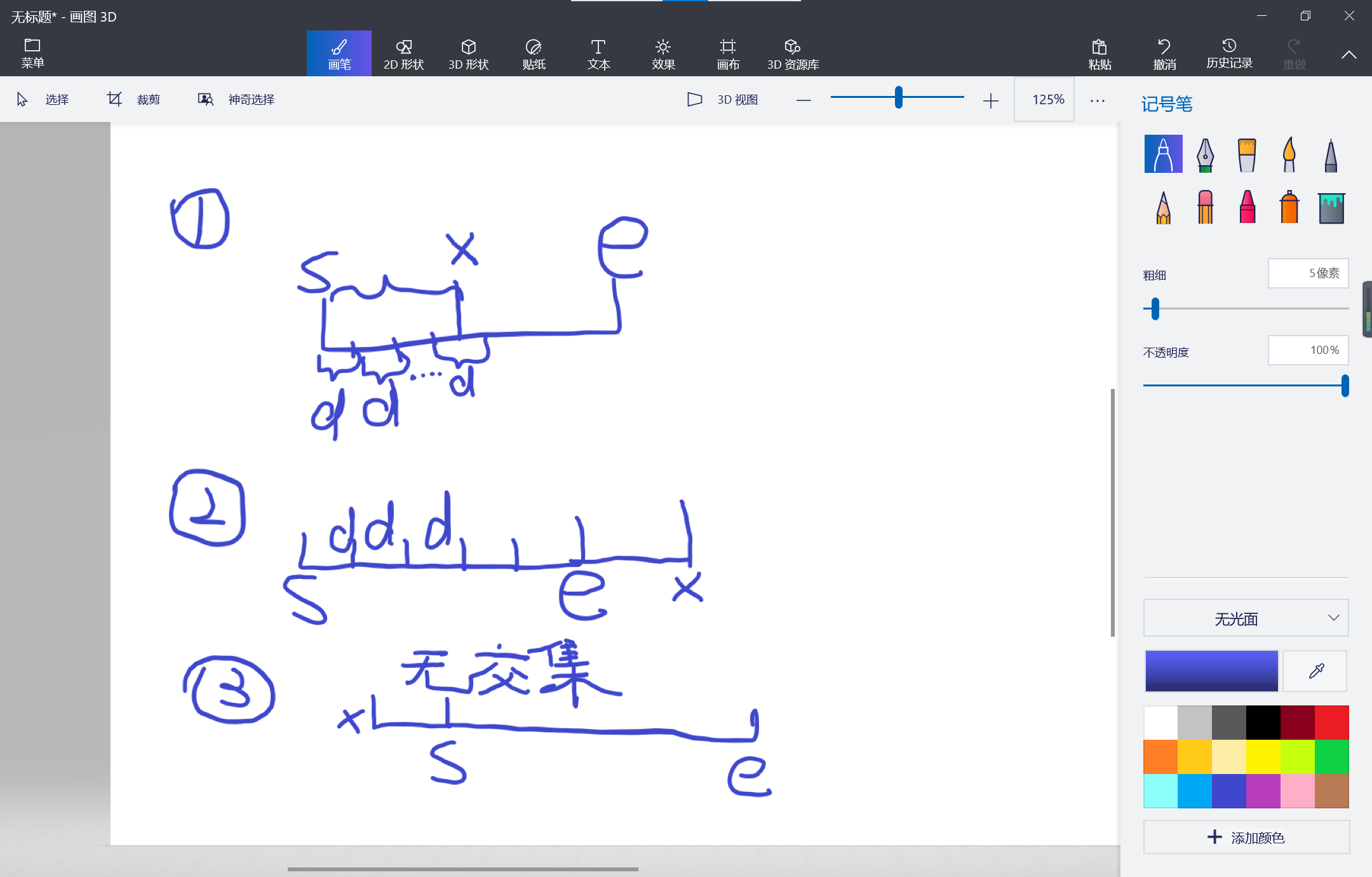
//而防线这道题用的分界性是在只有一个奇数的情况下其他都是偶数那必有一段的总和为偶数一段的总和为奇数

struct defe
{
    int s,e,d;
}a[N];
int n,t;



int getsum(int x)//因为开不了那么大的数组所以可以用一个变量多次计算
{int sum=0;
    for(int i=0;i<n;i++)
    {if(x>=a[i].s)//判断条件别少
        sum+=(min(a[i].e,x)-a[i].s)/a[i].d+1;//加一是加上s这个数
    }
    return sum;
}



bool check(int l,int mid)
{
    return (getsum(mid)-getsum(l-1))&1;
}

int maxe=0;
for(int i=0;i<n;i++)
{
    cin>>a[i].s>>a[i].e>>a[i].d;
    maxe=max(maxe,a[i].e);//找到最大的e作为r的初始值


}
int l=0;
int r=maxe;
if(!(getsum(maxe)&1))cout<<"There's no weakness."<<endl;
 else 
{ while(l<r)
{
int mid=r+l>>1;
if(check(l,mid))r=mid;
else l=mid+1;
}
cout<<r<<" "<<getsum(r)-getsum(r-1)<<endl;
}
}
}