在看题之前,先想一个问题。
如果有 100个物品,背包容量为1e8。并且这100个物品的体积和价值都是1
在这种情况下,直接使用01背包的标准解法是会超时的。
问题的解决
在标准的01背包中
f[i][j] 代表着:在前i个物品中选择,体积**不超过**j的情况下的**最大价值**
它与g[i][j] 在前i个物品中选择,价值**至少**为j的情况下的**最小体积**。是不是有一定的关联
在求出g[i][j] 后,我对总价值进行**逆向**遍历,当出现g[i][j]**小于或者等于**题目给定的体积时
所对应的价值j,是不是就是我们要找的**最大价值**
注:这里的总价值题目一般不会给出,需要根据数据输入的价值进行累加之后得到。
题目
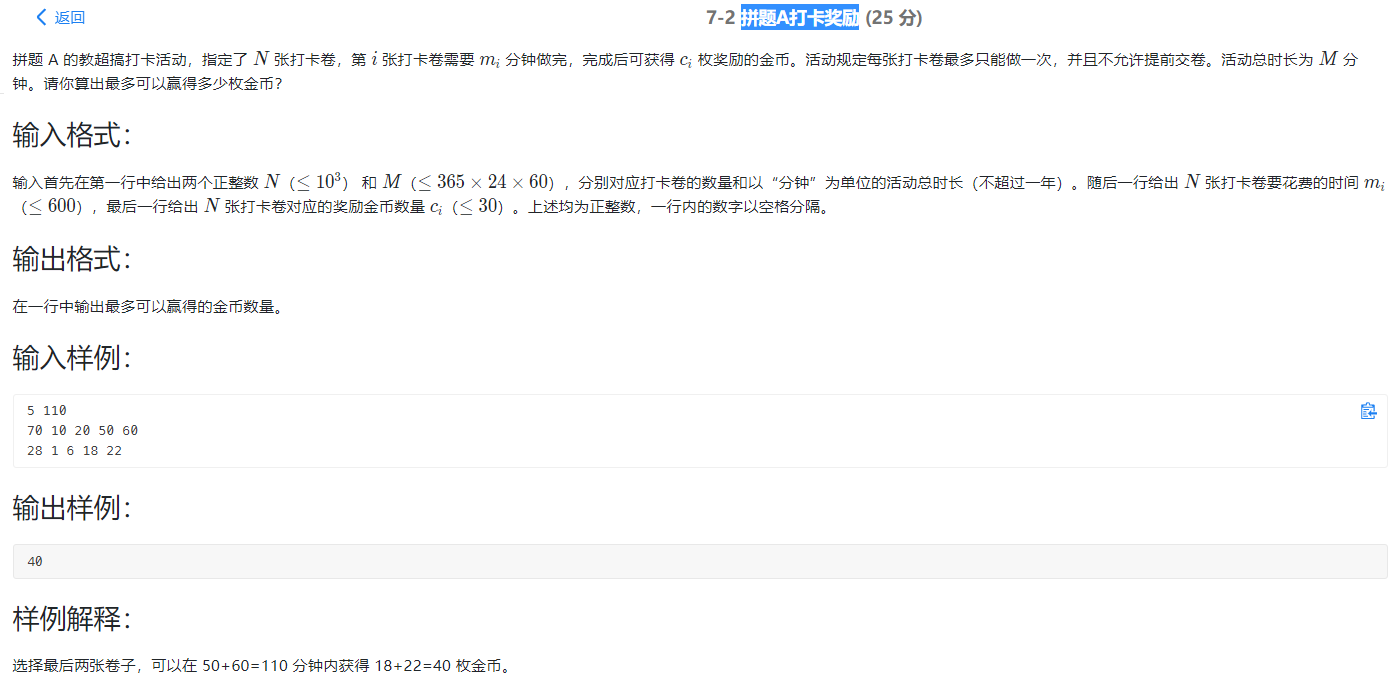
分析
这道题直接看时间复杂度 1000*365*24*60 是1e9级别的 会超时
但是来看总价值 1000*30 和100张卡片 是1e6级别的可以过
所以就得把价值当作花费,体积当作价值,进行逆向求解
f[i][j] 代表着 在前i个物品中选,花费(价值)至少为j的最小体积
算出来之后还需要逆序遍历一遍价值,来寻找体积小于等于要求的最大价值。
代码
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 30010;
int w[N], v[N], f[N];
int n, m, sum;
int main()
{
scanf("%d %d", &n, &m);
for (int i = 0; i < n; i++)
scanf("%d", &v[i]);
for (int i = 0; i < n; i++)
{
scanf("%d", &w[i]);
sum += w[i];
}
memset(f, 0x3f, sizeof f);
f[0] = 0;
for (int i = 0; i <= n; i++)
for (int j = sum; j >= 0; j--)
f[j] = min(f[j], f[max(0, j - w[i])] + v[i]);
//这里的核心代码参考了 潜水员问题(提高课里面的)
//也可以把j的循环条件改为 j>=w[i]
int ans = 0;
for (int j = sum; j >= 0; j--)
{
if (f[j] <= m)
{
printf("%d", ans);
break;
}
}
}