口诀：相同为 $0$，不同为 $1$

异或的性质：

• 位运算，不同位之间不影响
• $x \oplus 0 = x$
• $0 \oplus x = x$

最大异或

给定 $n$ 个数，要求你从中选出两个数，使得它们异或最大

分析：

暴力：枚举第一个数，然后在其左边找出与其异或值最大的那个数，复杂度为 $O(n^2)$
加速：在确定了第一个数的位置时，快速计算第二个数的最优选择
考虑固定一个数 $x$，然后把它左边的所有数建 Trie树 （字典树）

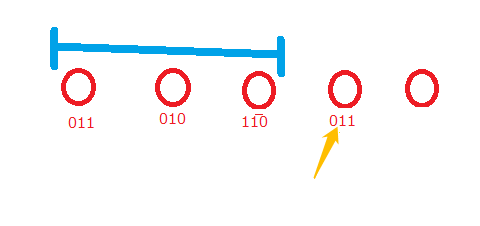
从高位到低位贪心：尽可能取与 $x$ 的二进制表示中相应位相反的数，把它与 $x$ 异或一下更新答案

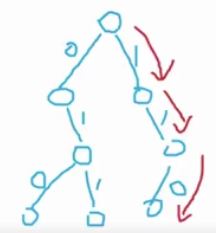
再把 $x$ 加入到 Trie树 中，黄色箭头向后移动，然后做之前类似的操作

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using std::cin;
using std::cout;

const int M = 3000005;

int son[M][2], idx;

void insert(int x) {
    int p = 0;
    for (int i = 30; i >= 0; --i) {
        int &s = son[p][x>>i&1];
        if (!s) s = ++idx; // 创建新节点 
        p = s;
    }
}

int query(int x) {
    int res = 0, p = 0;
    for (int i = 30; i >= 0; --i) {
        int s = x>>i&1;
        if (son[p][!s]) {
            res += 1<<i;
            p = son[p][!s];
        }
        else p = son[p][s];
    }
    return res;
}

inline void chmax(int& x, int y) { if (x < y) x = y; }

int main() {
    int n;
    cin >> n;

    int ans = 0;
    rep(i, n) {
        int a;
        cin >> a;
        chmax(ans, query(a));
        insert(a);
    }

    cout << ans << '\n';

    return 0;
}

异或第 $k$ 大

给定 $n$ 个数，求他们随意异或（任意多数）所能够得到所有数中第 $k$ 大是多少？

结论1：

将 $n$ 个数中任意数替换成它与其他若干数的异或，生成集合不变

$[x, y, z]$ 生成 $[x, y, z, x \oplus y, y \oplus z, x \oplus z, x \oplus y \oplus z]$
$[x, y, z \oplus x]$ 生成 $[x, y, z \oplus x, x \oplus y, x \oplus z \oplus x, y \oplus z \oplus x, x \oplus y \oplus z \oplus x] = [x, y, z \oplus x, x \oplus y, z, y \oplus z \oplus x, y \oplus z]$

结论2：

如果 $n$ 个数中某个数可以由其他数异或得到，那么这个数没用

$[010, 110, 100]$ 生成 $[010, 110, 100, 100, 110, 010, 000]$
去重后得到 $[010, 110, 100, 000]$
由 $010 \oplus 110 = 100$，所以可以把 $100$ 去掉
$[010, 110] \to [010, 110, 100]$

数列之异或

结论：

当 $n \% 4 == 1$ 时，$\oplus_{k=1}^n \ k = 1$
当 $n \% 4 == 2$ 时，$\oplus_{k=1}^n \ k = n+1$
当 $n \% 4 == 3$ 时，$\oplus_{k=1}^n \ k = 0$
当 $n \% 4 == 0$ 时，$\oplus_{k=1}^n \ k = n$

Code：

#include <bits/stdc++.h>

using std::cin;
using std::cout;
using ll = long long;

int main() {
    ll n;
    cin >> n;

    if (n % 4 == 1) cout << "1\n";
    else if (n % 4 == 2) cout << n+1 << '\n';
    else if (n % 4 == 3) cout << "0\n";
    else cout << n << '\n'; 

    return 0;
}

异或序列

可以按位考虑

我们可以先预处理出前缀异或和 $S_i$，对于区间 $[l, r]$ 的异或值就是 $S_{l-1} \oplus S_r$，而这等价于 该位上有多少个区间的异或值等于 $1$，我们可以统计出 $S[0 \cdots N]$ 在该位上有多少个 $1$ 以及多少个 $0$，二者的乘积就是这一位对答案的贡献

Code：

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using std::cin;
using std::cout;
using std::vector;
using ll = long long;

int main() {
    int n;
    cin >> n;

    vector<int> a(n);
    rep(i, n) cin >> a[i];
    vector<int> s(n+1);
    rep(i, n) s[i+1] = s[i] ^ a[i];

    ll ans = 0;
    rep(b, 30) {
        int odd = 0;
        rep(i, n+1) odd += s[i]>>b&1;
        ans += (ll)odd * (n+1 - odd) << b;
    }

    cout << ans << '\n';

    return 0;
}