目录
1. $dfs$与$bfs$
2. 树与图的遍历; 拓扑排序
- 树与图的存储
- 树和图的遍历
- 拓扑排序
3. 最短路问题
3.1 单源最短路问题
3.1.1 所有边都是正数
- 朴素版$dijkstra$ : 适用于稠密图 $O(n ^ 2)$
- 堆优化的$dijkstra$ : 适用于稀疏图 $O(m log n)$
3.1.2 边中存在负权
- bellman-ford算法 $O(mn)$
- $spfa$算法 一般是线性的,最坏$O(mn)$,容易被卡
A. $spfa$求最短路
B. $spfa$判断负环
3.2 多源汇最短路问题——$floyd$ $O(n ^ 3)$
4. 最小生成树
- $prim$算法 $O(n ^ 2 + m)$ 适合稠密图
- $kruskal$算法 $O(mlogm)$,适合稀疏图
5. 二分图
- 二分图的判断——染色法
- 二分图的匹配——匈牙利算法
正文
1. $dfs$与$bfs$
深度优先遍历就是一条路走到黑的遍历方式,可以想想对解的空间树从根节点到叶子结点的dfs,它的进行需要栈,一般采用递归实现,不过也可以自己手写栈(基本不会出现这种情况)
宽度优先遍历是遍历搜索解的空间树,一层一层遍历。它的进行需要队列,这里手写队列和用$stl$的队列都是可以的
宽搜相比深搜的一个优点就是它具有最短路的性质
思考搜索问题可以像$dp$那么思考,状态表示与状态转移(包含剪枝),不过还要额外思考什么时候停止搜索,尤其是$dfs$的递归终止条件一定要仔细思考,防止陷入死循环。宽搜的结束条件只需要思考结束状态是什么就可以,队列不无线增长是比较容易控制的
思考状态的表示,也就是解的空间树的每一个叶子的具体含义。$dfs$可以放在函数参数里面保存状态,$bfs$可以放到队列里面保存。不过对于比较大的数据,如大的数组,我们一般采用回溯法处理,也就是放在全局变量,用完要恢复现场
因为枚举的工作是指数级别的,所以我们需要考虑剪枝,就是对明显错误的答案进行舍弃,这样可以减少我们许多计算量
$dfs$大致框架
void dfs (state u)
{
st[u] = 1; // 剪枝,一般是状态数组,不过也可能是别的思路
for ( ; ; ) // 拓展结点
{
不重复,就拓展
dfs (state t);
}
}
$bfs$大致框架
int bfs()
{
q.push(start);
st[start] = 1;
while (q.size())
{
auto t = q.front(); q.pop();
if (t == end ) return ; // 找到答案,返回
for ( ; ; ) 拓展结点
{
不重复就入队
}
}
return ___ // 没有答案,返回
}
2. 树与图的遍历; 拓扑排序
2.1 树与图的存储
树是无环图,无向图是特殊的有向图。所以我们只需要知道有向图怎么存就可以了
(1) 邻接表
$g[a][b] = x$,表示$a$到$b$有一条边权为$x$的边
(2) 邻接表
下面列举的情况还考虑到了边的权重。其实我拿$acwing$的测试跑出来,$vector$存链表效率比手工模拟差距很小,有时候能五五开,甚至快一点。$vector$如果要存边的权重,那么里面存$pair$<$int, int$>$就行
// 对于每个点k,开一个单链表,存储k所有可以走到的点。h[k]存储这个单链表的头结点
int h[N], e[N], w[i], ne[N], idx;
// 添加一条边a->b
void add(int a, int b, int w)
{
e[idx] = b, w[idx] = w, ne[idx] = h[a], h[a] = idx ++ ;
}
// 初始化
idx = 0; // 定义在全局变量不用管
memset(h, -1, sizeof h);
2.2 树和图的遍历
时间复杂度 $O(n+m)$, $n$ 表示点数, $m$ 表示边数
这里是$dfs$和$bfs$思想在图里的一个简单应用
$dfs$
int dfs(int u)
{
st[u] = true; // st[u] 表示点u已经被遍历过
for (int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];
if (!st[j]) dfs(j);
}
}
$bfs$
queue<int> q;
st[1] = true; // 表示1号点已经被遍历过
q.push(1);
while (q.size())
{
int t = q.front();
q.pop();
for (int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if (!st[j])
{
st[j] = true; // 表示点j已经被遍历过
q.push(j);
}
}
}
2.3 拓扑排序
- 读入边的时候同时记录每个点的入度
- topsort()函数内,先将所有入度为0的点入队
- 取出队头元素,将队头元素的临边入度减1,如果为0,就入队。这么做知道队列为空
- 这样,出队的元素,按照顺序就是拓扑排序的结果,如果出队元素数量小于结点总数,那么拓扑序列不存在。注意,拓扑序列是不唯一的
为了省事,我们采用模拟队列,因为模拟队列的删除是懒惰删除,所以其实拓扑序列是保存在数组的,最后存在直接输出就好了
bool topsort()
{
int hh = 0, tt = -1;
// d[i] 存储点i的入度
for (int i = 1; i <= n; i ++ )
if (!d[i])
q[ ++ tt] = i;
while (hh <= tt)
{
int t = q[hh ++ ];
for (int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if (-- d[j] == 0)
q[ ++ tt] = j;
}
}
// 如果所有点都入队了,说明存在拓扑序列;否则不存在拓扑序列。
return tt == n - 1;
}
3. 最短路问题
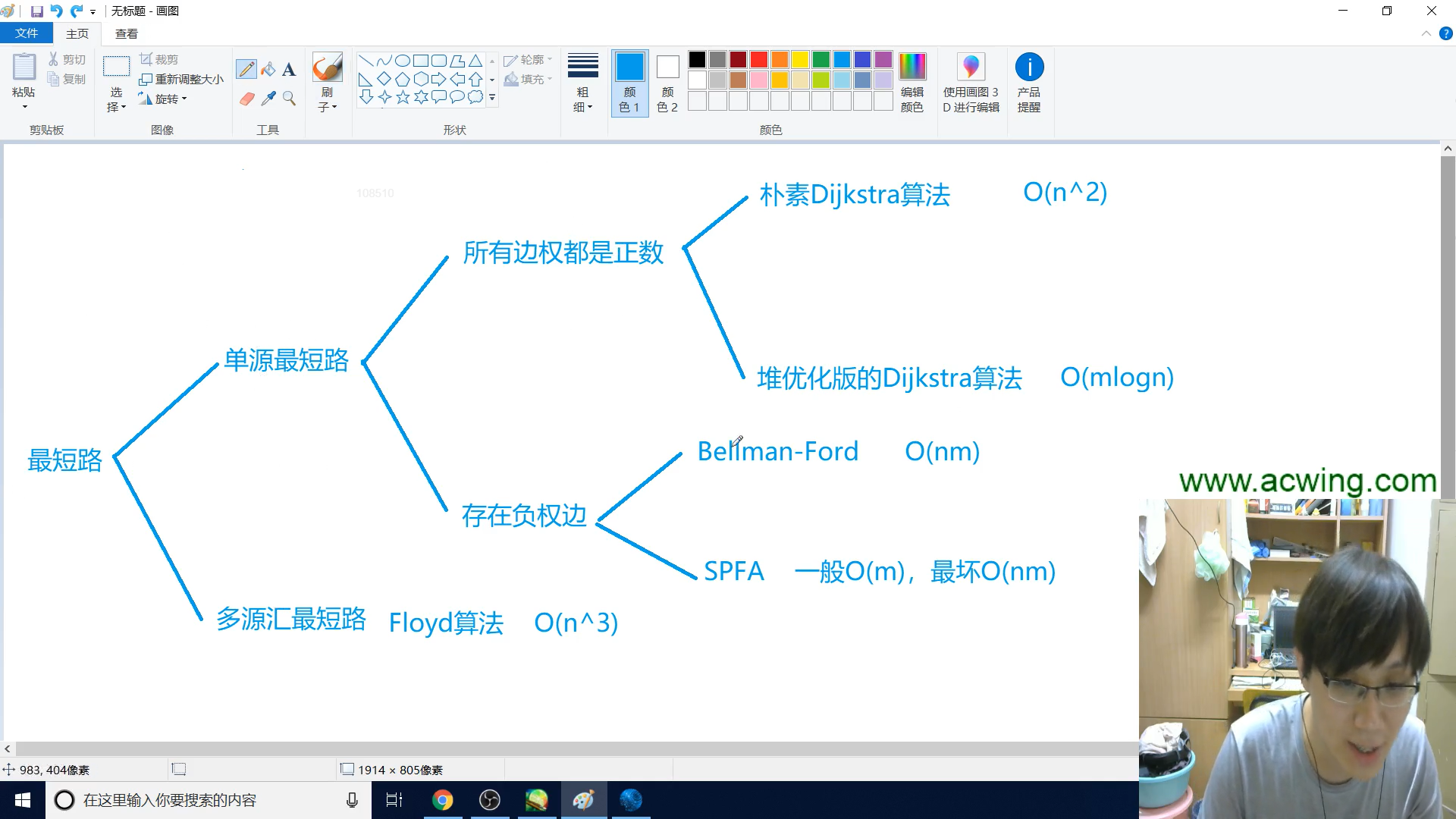
3.1 单元最短路
3.1.1 所有边都是正数
朴素版$dijkstra$ : 适用于稠密图 $O(n ^ 2)$
图的存储:邻接矩阵
- 将$dist$[ ]初始化为正无穷,起点的$dist$设置为0
- 迭代$n$次,首先找出当前没有确定最短距离点中距离起点最近的点
- 随后,将它纳入集合,用它来更新别的点到起点的最短距离。
这么操作$n$次,所有的点就被纳入集合了(由于最后一次不会有距离更新,所以y总写的是$n - 1$)
int g[N][N]; // 存储每条边
int dist[N]; // 存储1号点到每个点的最短距离
bool st[N]; // 存储每个点的最短路是否已经确定
// 求1号点到n号点的最短路,如果不存在则返回-1
int dijkstra()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
for (int i = 0; i < n - 1; i ++ )
{
int t = -1; // 在还未确定最短路的点中,寻找距离最小的点
for (int j = 1; j <= n; j ++ )
if (!st[j] && (t == -1 || dist[t] > dist[j]))
t = j;
// 用t更新其他点的距离
for (int j = 1; j <= n; j ++ )
dist[j] = min(dist[j], dist[t] + g[t][j]);
st[t] = true;
}
if (dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
堆优化的$dijkstra$ : 适用于稀疏图 $O(m log n)$
整体思路与朴素版一样,唯一区别是找最短距离的时候,我们是取得堆顶而不是遍历数组查找
图的存储:邻接表
typedef pair<int, int> PII;
int n; // 点的数量
int h[N], w[N], e[N], ne[N], idx; // 邻接表存储所有边
int dist[N]; // 存储所有点到1号点的距离
bool st[N]; // 存储每个点的最短距离是否已确定
// 求1号点到n号点的最短距离,如果不存在,则返回-1
int dijkstra()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
priority_queue<PII, vector<PII>, greater<PII>> heap;
heap.push({0, 1}); // first存储距离,second存储节点编号
while (heap.size())
{
auto t = heap.top();
heap.pop();
int ver = t.second, distance = t.first;
if (st[ver]) continue;
st[ver] = true;
for (int i = h[ver]; i != -1; i = ne[i])
{
int j = e[i];
if (dist[j] > distance + w[i])
{
dist[j] = distance + w[i];
heap.push({dist[j], j});
}
}
}
if (dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
3.1.2 边中存在负权
bellman-ford算法 $O(mn)$
边的存储:结构体
我们对每一个边都要进行一次松弛操作,迭代n次代表中间经过不超过n条边的最短路,迭代是有实际意义的
因为这里会更新不可达的点而且边存在负权,所以判断能否到达的条件是大于一个很大的数
int n, m; // n表示点数,m表示边数
int dist[N]; // dist[x]存储1到x的最短路距离
struct Edge // 边,a表示出点,b表示入点,w表示边的权重
{
int a, b, w;
}edges[M];
// 求1到n的最短路距离,如果无法从1走到n,则返回-1。
int bellman_ford()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
// 如果第n次迭代仍然会松弛三角不等式,就说明存在一条长度是n+1的最短路径,由抽屉原理,路径中至少存在两个相同的点,说明图中存在负权回路。
for (int i = 0; i < n; i ++ )
{
for (int j = 0; j < m; j ++ )
{
int a = edges[j].a, b = edges[j].b, w = edges[j].w;
if (dist[b] > dist[a] + w)
dist[b] = dist[a] + w;
}
}
if (dist[n] > 0x3f3f3f3f / 2) return -1;
return dist[n];
}
$spfa$算法 一般是线性的,最坏$O(mn)$,容易被卡
图的存储:邻接表(要遍历出边)
松弛操作中,只有起点的$dist$[ ]变化才能引起终点$dist$变化,所以不会更新不可达的点,最后判断是是否等于$0x3f3f3f3f$
- 起点的$dist$[ ] 为0, 并将起点入队
- 取出队头结点(它不在队列里面了),遍历它的临点,如果最短距离更新,并且它还不在队列中(剪枝)就入队
- 队列为空后,就求出起点到其它个点的最短距离了
int n; // 总点数
int h[N], w[N], e[N], ne[N], idx; // 邻接表存储所有边
int dist[N]; // 存储每个点到1号点的最短距离
bool st[N]; // 存储每个点是否在队列中
// 求1号点到n号点的最短路距离,如果从1号点无法走到n号点则返回-1
int spfa()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
queue<int> q;
q.push(1);
st[1] = true;
while (q.size())
{
auto t = q.front();
q.pop();
st[t] = false;
for (int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if (dist[j] > dist[t] + w[i])
{
dist[j] = dist[t] + w[i];
if (!st[j]) // 如果队列中已存在j,则不需要将j重复插入
{
q.push(j);
st[j] = true;
}
}
}
}
if (dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
$spfa$判负环
这是spfa的一个常见应用,基于容斥原理,如果最短路经过的边条数为$n$,那么经过的点是$n + 1$,则必然存在负环
这只需要在$spfa$算法上维护一个$cnt$[ ]数组,记录每一点最短值经过的边数即可,大于$n$则表示有最短路
int n; // 总点数
int h[N], w[N], e[N], ne[N], idx; // 邻接表存储所有边
int dist[N], cnt[N]; // dist[x]存储1号点到x的最短距离,cnt[x]存储1到x的最短路中经过的点数
bool st[N]; // 存储每个点是否在队列中
// 如果存在负环,则返回true,否则返回false。
bool spfa()
{
/* 不需要初始化dist数组
原理:如果某条最短路径上有n个点(除了自己), 那么加上自己之后一共有n+1个点,由抽屉原理一定有两个点相同,所以存在环*/
queue<int> q;
for (int i = 1; i <= n; i ++ )
{
q.push(i);
st[i] = true;
}
while (q.size())
{
auto t = q.front();
q.pop();
st[t] = false;
for (int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if (dist[j] > dist[t] + w[i])
{
dist[j] = dist[t] + w[i];
cnt[j] = cnt[t] + 1;
if (cnt[j] >= n) return true;
// 如果从1号点到x的最短路中包含至少n个点(不包括自己),则说明存在环
if (!st[j])
{
q.push(j);
st[j] = true;
}
}
}
}
return false;
}
3.2 多源汇最短路问题
$floyd$算法 $O(n ^ 3)$
三重循环很好记,这里是动态规划的思想
$f[i, j, k]$表示从$i$走到$j$的路径上除$i$和$j$点外只经过$1$到$k$的点的所有路径的最短距离。那么$f[i, j, k] = min(f[i, j, k - 1), f[i, k, k - 1] + f[k, j, k - 1]$,所以$k$必须要从小到大循环,内部循环顺序也是如此
初始化:
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= n; j ++ )
if (i == j) d[i][j] = 0;
else d[i][j] = INF;
// 算法结束后,d[a][b]表示a到b的最短距离
void floyd()
{
for (int k = 1; k <= n; k ++ )
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= n; j ++ )
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
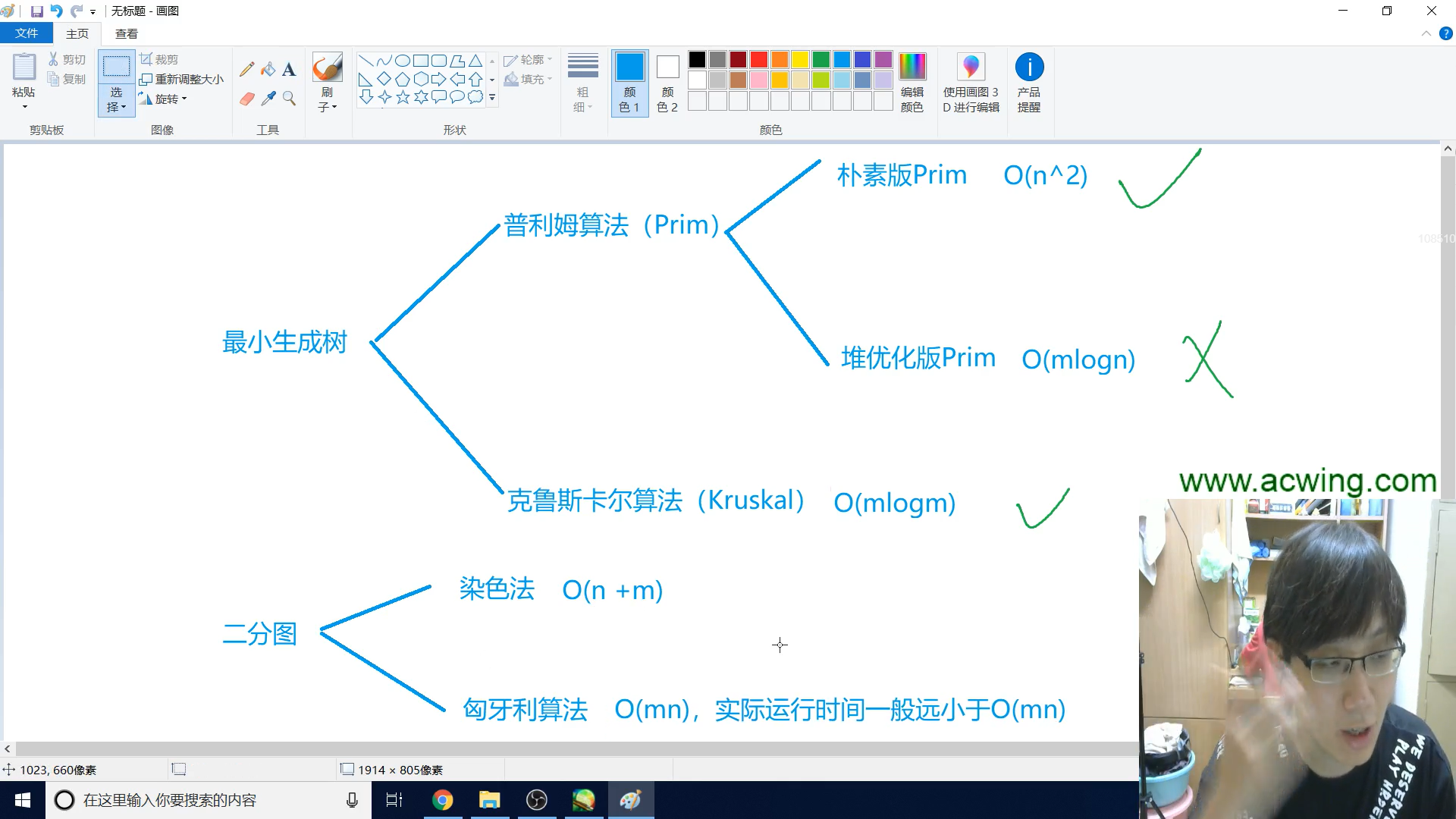
4. 最小生成树
4.1 $prim$算法 $O(n ^ 2 + m)$ 适合稠密图
图的存储:邻接矩阵
集合S:当前构成最小生成树的所有点
我们每次从集合外选出一个距离集合距离最近的点,将它纳入集合(最短距离对应的边就是构成最小生成树的边),并以此点去更新其他集合外的点到集合的最短距离,直到找完当前连通块内的所有点
如果不存在最小生成树,就是(非第一个点)集合外距离集合最近的点到集合距离为正无穷
每次迭代,确定一个点,所以迭代$n$次
int n; // n表示点数
int g[N][N]; // 邻接矩阵,存储所有边
int dist[N]; // 存储其他点到当前最小生成树的距离
bool st[N]; // 存储每个点是否已经在生成树中
// 如果图不连通,则返回INF(值是0x3f3f3f3f), 否则返回最小生成树的树边权重之和
int prim()
{
memset(dist, 0x3f, sizeof dist); // dist初始化为正无穷
int res = 0;
for (int i = 0; i < n; i ++ )
/* dijkstra是n - 1,是因为找到剩一个点时候,它不需要在计算了。而这里的n,
最后剩一个点的时候,答案还是要加入边的,所以最后一个点必须实实在在的计算
一遍所以迭代n次*/
{
int t = -1;
for (int j = 1; j <= n; j ++ )
if (!st[j] && (t == -1 || dist[t] > dist[j]))
t = j;
if (i && dist[t] == INF) return INF; // 如果是第一次,那么肯定是无穷,此时不应该返回无穷
if (i) res += dist[t]; // 不是第一次,就把这条边加进去。第一次是不存在边的,不应该计算
st[t] = true; // 标记下该点已经到达
for (int j = 1; j <= n; j ++ ) dist[j] = min(dist[j], g[t][j]); // 更新其他点到集合的最短距离
}
return res; // 返回最小生成树的边权重之和
}
4.2 $kruskal$算法 $O(mlogm)$,适合稀疏图
图的存储:结构体,由于要对边排序,需要重载小于号
先对边按边权值排序,从小到大选边,如果这个边的两个点不全在当前生成树的集合,那么就把他们加入到当前生成树的集合内,对应的边构成最小生成树
由于需要查询集合,所以要使用并查集
int n, m; // n是点数,m是边数
int p[N]; // 并查集的父节点数组
struct Edge // 存储边
{
int a, b, w;
bool operator< (const Edge &W)const // 运算符重载
{
return w < W.w;
}
}edges[M];
int find(int x) // 查询祖宗结点 + 路径压缩
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
int kruskal()
{
sort(edges, edges + m);
for (int i = 1; i <= n; i ++ ) p[i] = i; // 初始化并查集
int res = 0, cnt = 0;
for (int i = 0; i < m; i ++ )
{
int a = edges[i].a, b = edges[i].b, w = edges[i].w;
a = find(a), b = find(b);
if (a != b) // 如果两个连通块不连通,则将这两个连通块合并
{
p[a] = b; // 合并集合
res += w;
cnt ++ ; // 记录边数
}
}
if (cnt < n - 1) return INF; // 边数小于 n - 1,不存在最小生成树
return res;
}
5. 二分图
5.1 二分图的判断:染色法
二分图存在当且仅当不存在奇数环
算法流程
我们用$color$[ ]数组记录每一个点它染得颜色,对于任意一个连通块来说,只要其中一个点的颜色确认了,那么其他点的颜色都可以确认。
我们染色时(遍历),如果该点没被染色,那我们就去染色。如果染色了,就看是不是存在冲突,如果冲突了,染色失败,不存在二分图,反之存在二分图。
因为给的图不一定是一个连通块,所以我们要对每个点都要遍历一遍(遍历过的进行标记,防止二次遍历)
int n; // n表示点数
int h[N], e[M], ne[M], idx; // 邻接表存储图
int color[N]; // 表示每个点的颜色,-1表示未染色,0表示白色,1表示黑色
// 参数:u表示当前节点,c表示当前点的颜色
bool dfs(int u, int c)
{
color[u] = c;
for (int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];
if (color[j] == -1)
{
if (!dfs(j, !c)) return false;
}
else if (color[j] == c) return false;
}
return true;
}
bool check()
{
memset(color, -1, sizeof color);
bool flag = true;
for (int i = 1; i <= n; i ++ )
if (color[i] == -1)
if (!dfs(i, 0))
{
flag = false;
break;
}
return flag;
}
4.2 二分图的匹配:匈牙利算法
算法流程
$1.$ 对于任何一个男孩(对于每一个左半部的点执行$find$操作)
$2.$ 依次看看和他相互有好感值的女生(遍历它的临边), 如果在当前这个男生还没有考虑过这个女生(没有判断是否可以配对),
$(1)$ 如果女生还没有找到配对的男生($match$[ ]为0),那么好,他们可以凑成一对
$(2)$ 如果女生找到了配对的男生($match$[ ]不为0),那么我们看看那个男生可不可以换一个女生配对,给当前这个男生一个机会,如果原来配对的男生可以换一个下家(递归尝试原来配对的男生),那么当前这个女生就和当前的男生进行配对
通过以上步骤,我们就可以让这么多男生女生里面获得最多的人成双成对(也就是达到二分图的最大匹配)
int n1, n2; // n1表示第一个集合中的点数,n2表示第二个集合中的点数
int h[N], e[M], ne[M], idx;
/*邻接表存储所有边,匈牙利算法中只会用到
从第一个集合指向第二个集合的边,所以这里只用存一个方向的边*/
int match[N]; // 存储第二个集合中的每个点当前匹配的第一个集合中的点是哪个
bool st[N]; // 表示第二个集合中的每个点是否已经被遍历过
bool find(int x)
{
for (int i = h[x]; i != -1; i = ne[i])
{
int j = e[i];
if (!st[j])
{
st[j] = true;
if (match[j] == 0 || find(match[j]))
{
match[j] = x;
return true;
}
}
}
return false;
}
// 求最大匹配数,依次枚举第一个集合中的每个点能否匹配第二个集合中的点
int res = 0;
for (int i = 1; i <= n1; i ++ )
{
memset(st, false, sizeof st);
if (find(i)) res ++ ;
}

