求解方程组

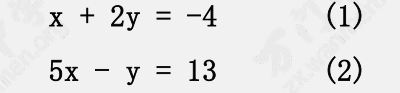
$(2) - (1) \times 5$ 得到 $-11y = 33$
于是 $y = -3$
代入 $(1)$ 得到 $x = 2$

方程组可以写成矩阵的形式：

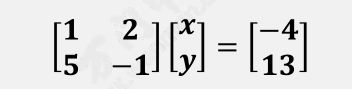
然后通过转换得到了：

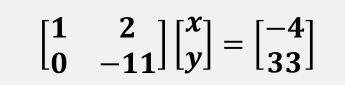
这个时候左边是上三角矩阵，可以轻松的从下往上推出每个未知数的解。

高斯消元法

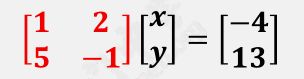
左边的这个矩阵就是系数矩阵。
高斯消元法就是通过一系列操作把系数矩阵转化成上三角矩阵，然后依次算出未知数的过程，非常的直观。

一般化的形式：
一开始有 $n$ 个方程和 $n$ 个未知数。

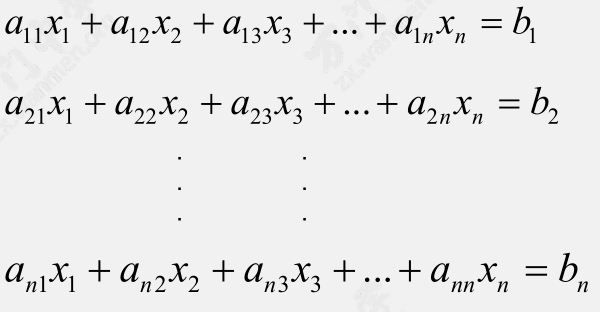
对于第 $1$ 个方程，乘上 $a_{21}$ 除以 $a_{11}$

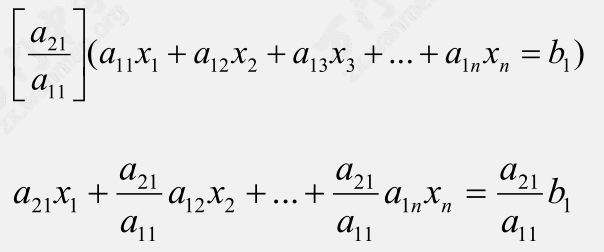
然后用第二个方程减去上一个结果

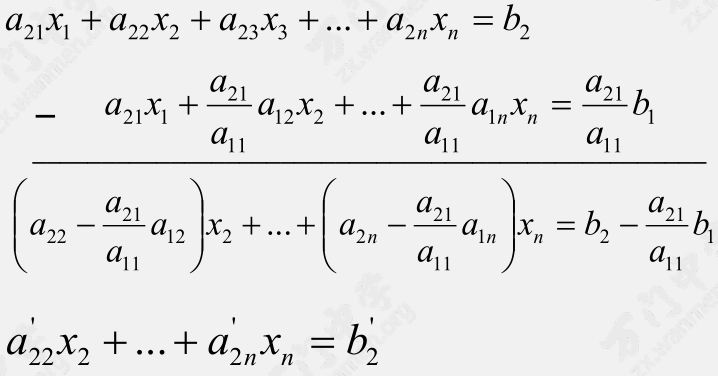
重复以上两步，对第 $3 \sim n$ 行都做一遍。

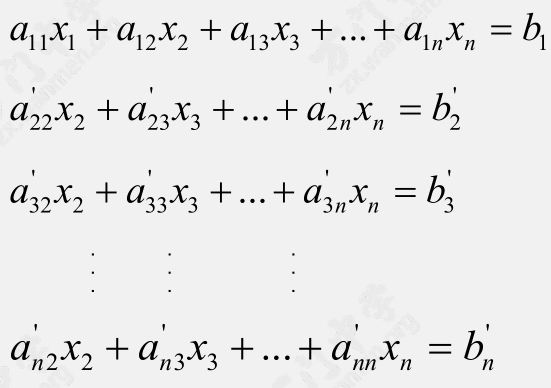
然后用第 $2$ 行去消第 $3 \sim n$ 行

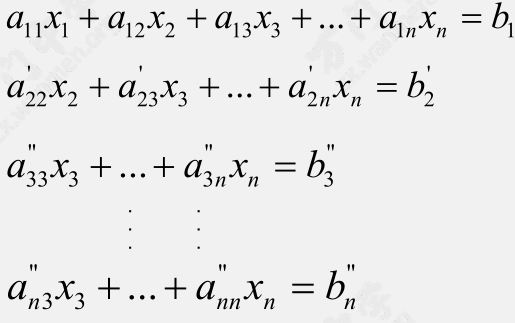
直到最后一行

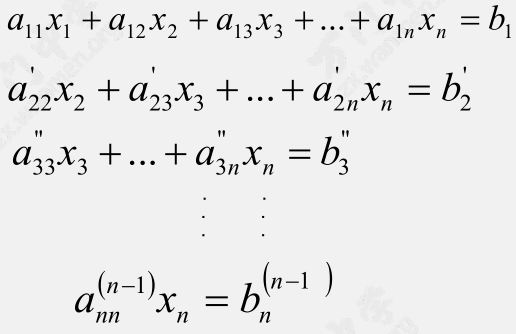
矩阵形式：

倒推出 $x_n, x_{n-1}, \cdots, x_1$

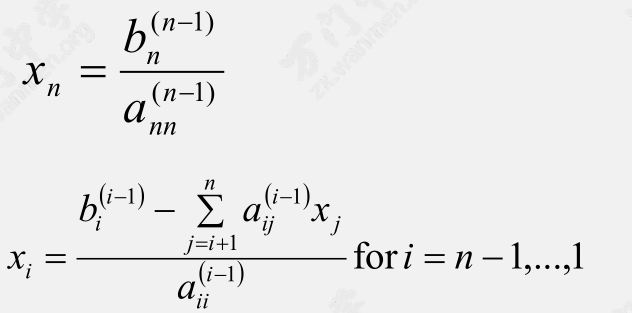
代码实现

我们用 $n \times (n+1)$ 的矩阵来存系数和等号右边的数
等号右边的数存在第 $n+1$ 列

double matrix[N][N];

void gauss(int n) {
    // 把系数矩阵变上三角矩阵 
    for (int i = 1, pos; i <= n; ++i) { // pos 用来找 xi 的非零系数 
        for (pos = i; fabs(a[pos][i]) > eps; ++pos);
        for (int j = i; j <= n+1； ++j) swap(a[pos][j], a[i][j]);
        for (int j = i+1; j <= n; ++j) {
            if (fabs(a[j][i]) > eps) {
                double p = a[i][j] / a[i][i];
                for (int k = i; k <= n+1; ++k) a[j][k] = a[i][k] - a[j][k] * p;
            }
        }
    }
    for (int i = n; i >= 1; --i) {
        x[i] = a[i][n+1];
        for (int j = i+1; j <= n; ++j) x[i] -= x[j] * a[i][j];
        x[i] /= a[i][i];
    }
}

可以发现高斯消元总共有 $3$ 层循环。
时间复杂度就是 $O(n^3)$。

自由元

如果最外层枚举 $i$ 的时候，发现没有一个 $a[j][i]$ 非零，说明 $a[j][i]$ 的系数是 $0$
如果在第二步倒推 $x$ 的值的时候等式右边也消成了 $0$，即 $0 \times x[i] = 0$
也就是 $x[i]$ 取任何值都不会影响这个方程组
我们称此时的 $x[i]$ 为自由元
一旦有自由元，就说明方程有无数解。

但是如果在第二步倒推 $x$ 的值的时候等式右边也消成了非 $0$ 值，即 $0 \times x[i] = k (k \neq 0)$
也就是 $x[i]$ 取任何值都不能满足这个方程组
此时这个方程组无解。

应用

高斯消元同样可以用来解 ${\rm xor}$ 方程组
只要把加减法改成 ${\rm xor}$ 即可
每个系数/未知数的取值是 $0$ 或 $1$
此时如果方程有 $k$ 个自由元，那么就一共有 $2^k$ 组解

模意义下的方程组依然可以求解
除法那步需要改变
可以改为乘逆元
或者求出两个数的 ${\rm LCM}$，两个方程分别乘一个系数，使得两式的第一个系数均为 ${\rm LCM}$，就可以相减消掉一个了。

例1：【模板】高斯消元法

Code：

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using std::cin;
using std::cout;

const int MX = 105;
const double eps = 1e-8;

int n;
double A[MX][MX];

int gauss() {
    int c, r;
    for (c = 0, r = 0; c < n; ++c) {
        int t = c;
        for (int i = r; i < n; ++i) {
            if (fabs(A[i][c]) > fabs(A[t][c]))
                t = i;
        }

        if (fabs(A[t][c]) < eps) continue;

        for (int i = c; i <= n; ++i) std::swap(A[t][i], A[r][i]);

        for (int i = n; i >= c; --i) A[r][i] /= A[r][c];
        for (int i = r+1; i < n; ++i) {
            if (fabs(A[i][c]) > eps) {
                for (int j = n; j >= c; --j) {
                    A[i][j] -= A[r][j] * A[i][c];
                }
            }
        } 
        r++;
    }

    if (r < n) {
        for (int i = r; i < n; ++i) {
            if (fabs(A[i][n]) > eps) 
                return 2; // 无解 
        } 
        return 1; //有无穷多组解 
    }

    for (int i = n-1; i >= 0; --i) {
        for (int j = i+1; j < n; ++j) {
            A[i][n] -= A[i][j] * A[j][n];
        }
    }

    return 0; // 有唯一解 
}

int main() {
    cin >> n;
    rep(i, n)rep(j, n+1) cin >> A[i][j];

    int t = gauss();
    if (t) puts("No Solution"); 
    else {
        rep(i, n) printf("%.2lf\n", A[i][n]);
    }

    return 0;
}

例2：[SDOI2006]线性方程组

Code：

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using std::cin;
using std::cout;

const int MX = 105;
const double eps = 1e-8;

int n;
double A[MX][MX];

int gauss() {
    int c, r;
    for (c = 0, r = 0; c < n; ++c) {
        int t = c;
        for (int i = r; i < n; ++i) {
            if (fabs(A[i][c]) > fabs(A[t][c]))
                t = i;
        }

        if (fabs(A[t][c]) < eps) continue;

        for (int i = c; i <= n; ++i) std::swap(A[t][i], A[r][i]);

        for (int i = n; i >= c; --i) A[r][i] /= A[r][c];
        for (int i = r+1; i < n; ++i) {
            if (fabs(A[i][c]) > eps) {
                for (int j = n; j >= c; --j) {
                    A[i][j] -= A[r][j] * A[i][c];
                }
            }
        } 
        r++;
    }

    if (r < n) {
        for (int i = r; i < n; ++i) {
            if (fabs(A[i][n]) > eps) 
                return 2; // 无解 
        } 
        return 1; //有无穷多组解 
    }

    for (int i = n-1; i >= 0; --i) {
        for (int j = i+1; j < n; ++j) {
            A[i][n] -= A[i][j] * A[j][n];
        }
    }

    return 0; // 有唯一解 
}

int main() {
    cin >> n;
    rep(i, n)rep(j, n+1) cin >> A[i][j];

    int t = gauss();
    if (t == 0) {
        rep(i, n) printf("x%d=%.2lf\n", i+1, A[i][n]);
    }
    else if (t == 1) puts("0");
    else puts("-1");

    return 0;
}

例3： 【模板】矩阵求逆

首先只有方阵（行数和列数一样）才能讨论求逆
其次，给出 $n$ 阶方阵 $A$，求解其逆矩阵的方法如下：

• 在方阵 $A$ 的右边加一个单位矩阵构成 $n \times 2n$ 的矩阵 $(A, I_n)$
• 再用单位阵将其化简为最简行阶梯形矩阵 $(I_n, A_{-1})$，即可得到 $A$ 的逆矩阵 $A^{-1}$。若最终的行阶梯形矩阵的左半部分不是单位阵，则矩阵 $A$ 不可逆。

Code：

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using std::cin;
using std::cout;
using ll = long long;

const double eps = 1e-8;

int n;
ll A[405][805];

const int mod = 1000000007;
ll pow_mod(ll a, ll k) {
    ll res = 1;
    while (k) {
        if (k&1) res = res * a % mod;
        a = a * a % mod;
        k >>= 1;
    }
    return res;
}

void gauss() {
    int r;
    rep(i, n) {
        r = i;
        for (int j = i+1; j < n; ++j) { 
            if (A[j][i] > A[r][i])
                r = j;
        }
        if (r != i) std::swap(A[i], A[r]); // 把第 i 行到第 n-1 行的每行首个非零元最大的那一行交换上去 

        if (!A[i][i]) {
            puts("No Solution");
            return;
        }

        int x = pow_mod(A[i][i], mod-2);
        rep(k, n) {
            if (k == i) continue;
            int t = A[k][i] * x % mod;
            for (int j = i; j < 2*n; ++j) {
                A[k][j] = ((A[k][j] - t * A[i][j]) % mod + mod) % mod;
            }
        }
        rep(j, 2*n) A[i][j] = A[i][j] * x % mod;
    }

    rep(i, n) {
        for (int j = n; j < 2*n; ++j) {
            cout << A[i][j] << " ";
        }
        cout << '\n';
    }
}

int main() {
    cin >> n;
    rep(i, n) {
        rep(j, n) cin >> A[i][j];
        A[i][i+n] = 1;
    }

    gauss();

    return 0;
}

例4： 【模板】行列式求值

先利用高斯消元把该行列式对应的矩阵化成上三角矩阵，而该行列式的值就是所有对角元的乘积。

Code：

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using std::cin;
using std::cout;
using ll = long long;

const int MX = 605;
ll A[MX][MX];

int main() {
    int n, p;
    cin >> n >> p;

    rep(i, n)rep(j, n) cin >> A[i][j];

    int rev = 1;
    rep(i, n) {
        for (int j = i+1; j < n; ++j) { // 第 j 行减去(第 i行乘以  A[j][i]/A[i][i])
            while (A[i][i]) {
                ll x = A[j][i] / A[i][i];
                rep(k, n) A[j][k] = (A[j][k] - x * A[i][k] % p + p) % p;
                std::swap(A[i], A[j]);
                rev *= -1;
            }
            std::swap(A[i], A[j]);
            rev *= -1;
        }
    }

    ll ans = rev;
    rep(i, n) ans = ans * A[i][i] % p;
    cout << (ans + p) % p << '\n';

    return 0;
} 

例5：高斯消元解异或线性方程组

1. 消成上三角矩阵：
   a. 枚举列
   b. 找非零行
   c. 交换
   d. 下面清零

2. 判断：唯一解、无解、无穷解

Code：

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using std::cin;
using std::cout;

const int MX = 105;

int n;
int A[MX][MX];

int gauss() {
    int r, c;
    for (r = c = 0; c < n; ++c) {
        int t = r;
        for (int i = r; i < n; ++i) {
            if (A[i][c]) {
                t = i;
                break;
            }
        }
        if (!A[t][c]) continue;

        std::swap(A[t], A[r]);

        for (int i = r+1; i < n; ++i) {
            if (!A[i][c]) continue;
            for (int j = c; j <= n; ++j) {
                A[i][j] ^= A[r][j];
            } 
        }
        r++;
    }

    if (r < n) {
        for (int i = r; i < n; ++i) {
            if (A[i][n]) return 2;
        }
        return 1;
    }

    for (int i = n-1; i >= 0; --i) {
        for (int j = i+1; j < n; ++j) {
            A[i][n] ^= A[i][j] * A[j][n];
        }
    }

    return 0;
}

int main() {
    cin >> n;
    rep(i, n)rep(j, n+1) cin >> A[i][j];

    int t = gauss();
    if (t == 0) {
        rep(i, n) cout << A[i][n] << '\n';
    }
    else if (t == 1) puts("Multiple sets of solutions");
    else puts("No solution");

    return 0;
}