一.基础概念

所谓递归函数 就是自己调用自己的函数（无限套娃）
eg：一个偶数与2的和还是一个偶数

二.一些知识点

1、函数定义与声明：一般来说有两种写法：一种写在主函数之前，一种写在主函数之后（即先声明，再具体实现），不过无论哪种写法，都要遵循函数先声明后操作的原则。其次：对于第二种写法在声明时一定注意加分号。

2、函数类型：bool、void、int……须要注意的是返回值一定要和函数类型相对应。

3、函数的调用及实参与形参间的传递：

①、传值调用：该种调用方法较简单，注意形参与实参间一一对应即可。

②、传引用：

        例如 int &a=b，可以理解为给b起了一个别名；当再次对a操作时即对b进行操作，例如a=6，这时b==6。

③、指针传递：

        例如 int *p，即定义了一个指向整形变量的指针p；若在定义时对其赋值，int *p=？，那么给p的应当是一个地址，之后再对其操作，如*p=6；表示给p所指向的变量赋值6。

④、数组的地址：

        最后，关于数组，因为其本身的特殊性，所以注意要几个小问题：比如，a[i]所表示的是具体的数值，而a+i表示的则是第i+1的元素的地址，同理，*（a+i）表示的就是一个数值了。

三.样例展示

>Fibonacci（斐波那契）

（又称兔子数列）
定义：数列的第一项和第二项都为1，从第三项开始第n项都等于n的前两项之和
$1,1, 2, 3, 5, 8, 13……$

#include<iostream>
using namespace std;
int fibonacci(int n){
    if(n<=2) return 1;
    else return fibonacci(n-1)+fibonacci(n-2);//递归函数，即第n项=(n-1)与(n-2)项之和

}
int main() {
    int n;
    cin>>n;
    cout<<fibonacci(n);
    return 0;
} 

>阶乘（敲黑板）

在数学中，符号 n! 表示数字 n 的阶乘。整数 n 的阶乘被定义如下

$n! = 1 \times 2 \times 3 \times … \times n$; 如果 n>0
n =1; 如果 n = 0

规则规定，当 n 大于 0 时，其阶乘是从 1 到 n 的所有正整数的乘积。例如，6! 可以计算为
$1 \times 2 \times 3 \times 4 \times 5 \times 6$规则还规定了基本情况：0 的阶乘是 1。

可以使用递归定义一个数的阶乘，如下所示：

factorial(n) = n X fafactorial(n-1); 如果 n> 0
factorial(n) = 1; 如果 n = 0

这个递归定义的 C++ 实现语句如下：

int factorial(int num)
{
    if (num == 0) //基本情况返回1;
        return 1;
    else
        return num * factorial(num - 1);
}

来看一个显示 3! 的值的程序，其语句如下：

cout << factorial(3) << endl;

第一次调用该函数时，num 被设置为 3，所以 if 语句将执行以下代码行：

return num * factorial(num - 1);

虽然这是一个 return 语句，但它并不会立即返回，这是因为在确定返回值之前，必须确定 factorial(num-1) 的值。该函数被递归调用，直到第 4 次调用，其中的 num 参数将被设置为 0。图 1 中直观地说明了函数每次调用期间 num 的值和返回值。

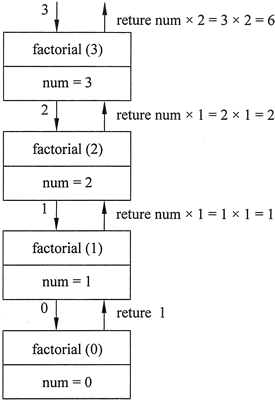
下面的程序演示了 factorial 函数的使用:

#include < iostream >
using namespace std;
// Function prototype
int factorial(int);
int main()
{
    int number;
    cin >> number;
    cout << number << ;
    cout << factorial (number) << endl;
    return 0;
}
int factorial(int num)
{
    if (num == 0) //base case
        return 1;
    else
        return num * factorial(num - 1);
} 

结束语：关于自己的生活，我和你都不是读者，而是作者。至少结局，还是能自己说了算的。————《银魂》