分析

扫描线模板题链接
- 这里将出现的所有矩形以横坐标为分割线划分成一个个竖直的长条，计算每个长条的面积，相加就可以得到答案，如下图：

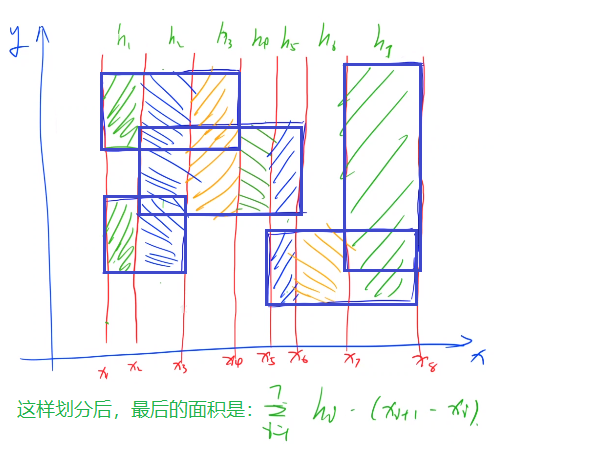
- 每个长条内部都是一堆等宽的小矩形，我们求出这些矩形在竖直方向上的长度，然后乘以宽度就是这个长条的面积。

• 如何求解每个长条竖直方向上的长度之和呢？首先遍历所有矩形，找到这个长条中所有的线段，然后使用区间合并即可。

• 关于区间合并可以参考：AcWing 803 区间合并。

• 本题的时间复杂度是：O(n2×log(n))O(n2×log(n))。

代码

#include <iostream>
#include <cstring>
#include <vector>
#include <algorithm>

#define x first
#define y second

using namespace std;

typedef long long LL;
typedef pair<int, int> PII;

const int N = 1010;

int n;
PII l[N], r[N];  // 存储矩形左下角和右上角坐标
PII q[N];  // 存储每个竖直长条中线段

// 计算一个竖直长条的面积
LL range_area(int a, int b) {

    // 求需要合并的区间
    int cnt = 0;
    for (int i = 0; i < n; i++)
        if (l[i].x <= a && r[i].x >= b)
            q[cnt++] = {l[i].y, r[i].y};
    if (!cnt) return 0;

    // 合并区间、求区间长度并
    sort(q, q + cnt);
    LL res = 0;
    int st = q[0].x, ed = q[0].y;
    for (int i = 1; i < cnt; i++)
        if (q[i].x <= ed) ed = max(ed, q[i].y);
        else {
            res += ed - st;
            st = q[i].x, ed = q[i].y;
        }
    res += ed - st;

    return res * (b - a);
}

int main() {

    scanf("%d", &n);
    vector<int> xs;
    for (int i = 0; i < n; i++) {
        scanf("%d%d%d%d", &l[i].x, &l[i].y, &r[i].x, &r[i].y);
        xs.push_back(l[i].x), xs.push_back(r[i].x);
    }

    sort(xs.begin(), xs.end());

    LL res = 0;
    for (int i = 0; i + 1 < xs.size(); i++)
        if (xs[i] != xs[i + 1])
            res += range_area(xs[i], xs[i + 1]);

    printf("%lld\n", res);

    return 0;
}