1. 子孙的个数

$\rm Ncik$ 有一颗 $N$ 个顶点的树，树的顶点编号为 $0$ 到 $N-1$，以顶点 $0$ 为根。此外，顶点 $i$ 的父节点为 $P_i(1 \leqslant i \leqslant N-1)$。
分别求出顶点 $i(i = 0, 1, \cdots, N-1)$ 的子孙个数。

• 子孙：在以顶点 $v$ 为根的子树所包含的所有点中，除点 $v$ 外都是 $v$ 的子孙

限制：

• $1 \leqslant N \leqslant 1000$
• $0 \leqslant P_i \leqslant i-1$

算法分析：

记 $S[v]$ 为以顶点 $v$ 为根的子树大小

$S[v] = 1 + \sum\limits_{u \ \text{为} \ v \ \text{的孩子}} S[u]$

也就是要求 $S[v]$，只需求出 $v$ 的所有孩子的 $S[u]$ 即可

C++ 代码：

#include <bits/stdc++.h>

using std::cin;
using std::cout;
using std::vector;

int main() {
    int n;
    cin >> n;

    vector<vector<int>> to(n);
    for (int v = 1; v < n; ++v) {
        int p;
        cin >> p;
        to[p].push_back(v);
    }

    vector<int> siz(n);
    auto dfs = [&](auto f, int v) -> void {
        for (int u : to[v]) {
            f(f, u);
        }

        siz[v] = 1;
        for (int u : to[v]) {
            siz[v] += siz[u];
        }
    };

    dfs(dfs, 0);

    for (int s : siz) cout << s-1 << '\n';

    return 0;
}

2. 树上匹配

给你一颗 $N$ 个节点的树
匹配是指一组边，其中每个点至多是一条边的端点
求在一个匹配中最多的边数（也就是匹配大小）

限制：

• $1 \leqslant n \leqslant 2 \times 10^5$
• $1 \leqslant a, b \leqslant n$

算法分析

考虑树形${\rm dp}$

记 dp[v][0/1] 表示在以顶点 $v$ 为根的子树中，$v$ 不与（与）自己孩子匹配的最大匹配数

转移方程：

记 $f[v] = \max(dp[v][0], dp[v][1])$ 表示以顶点 $v$ 为根的子树的最大匹配数

若顶点 $v$ 不与自己孩子匹配，对于其孩子节点 $u$ 而言无所谓是否选择和自己孩子匹配

$$ dp[v][0] = \sum\limits_{u \ \text{为} \ v \ \text{的孩子}} f[u] $$

若顶点 $v$ 选择与自己的某个孩子 $u$ 匹配，那么顶点 $u$ 就不能再和他的孩子匹配，至于 $v$ 的其他孩子则不关心他们的状态

$$ dp[v][1] = \max(dp[v][0] - f[u]) + dp[u][0] + 1 $$

不妨以顶点 $1$ 作为根节点
最后的答案就是 $\max(dp[1][0], dp[1][1])$

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using std::cin;
using std::cout;
using std::max;
using std::vector;

inline void chmax(int& x, int y) { if (x < y) x = y; }

int main() {
    int n;
    cin >> n;

    vector<vector<int>> to(n);
    rep(i, n-1) {
        int a, b;
        cin >> a >> b;
        --a; --b;
        to[a].push_back(b);
        to[b].push_back(a);
    }

    vector dp(n, vector<int>(2));
    auto dfs = [&](auto f, int v, int p=-1) -> void {
        for (int u : to[v]) {
            if (u == p) continue;
            f(f, u, v);
            dp[v][0] += max(dp[u][0], dp[u][1]);
        }

        for (int u : to[v]) {
            if (u == p) continue;
            chmax(dp[v][1], dp[v][0] - max(dp[u][0], dp[u][1]) + dp[u][0] + 1);
        } 
    };

    dfs(dfs, 0);

    int ans = max(dp[0][0], dp[0][1]);
    cout << ans << '\n';

    return 0;
}

3. 树的直径

给你一颗包含 $n$ 个点的树
树的直径是指两点之间的最长距离。你的任务是计算出树的直径。

限制：

• $1 \leqslant n \leqslant 2 \times 10^5$

算法分析：

做法有两种：跑两遍 dfs/bfs，或者树形dp

方法一：

在树上随便找一个点 $u$，从 $u$ 出发，找到距离它最远的点 $v$。再从 $v$ 出发，找到距离它最远的点 $w$（$w$有可能还是 $u$），则 $v$ 和 $w$ 之间的路径就是树的直径。

注意：这种做法无法处理负权边

方法二：

我们不妨枚举直径在树上转弯的点。所以我们维护出到一个节点向下的最长链和次长链，然后用二者相加和来更新答案，同时更新父亲节点的最长链和次长链。

这两种做法复杂度都为 $O(n)$

C++ 代码

// 做法1
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using std::cin;
using std::cout;
using std::vector;
using P = std::pair<int, int>;

int main() {
    int n;
    cin >> n;

    vector<vector<int>> to(n);
    rep(i, n-1) {
        int a, b;
        cin >> a >> b;
        --a; --b;
        to[a].push_back(b);
        to[b].push_back(a);
    }

    auto dfs = [&](auto f, int v, int d=0, int p=-1) -> P {
        P res(d, v); // res 维护从点 v 开始移动的距离和点 v 走到的终点 
        if (p == -1) res = P(0, -1);
        for (int u : to[v]) {
            if (u == p) continue;
            res = max(res, f(f, u, d+1, v));
        }
        return res;
    };

    int a = dfs(dfs, 0).second;
    int ans = dfs(dfs, a).first;
    cout << ans << '\n';

    return 0;
}

// 做法2：由于这里是无权边，所以只需开两个变量来维护最长链和次长链的长度即可
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using std::cin;
using std::cout;
using std::vector;

inline void chmax(int& x, int y) { if (x < y) x = y; }

int main() {
    int n;
    cin >> n;

    vector<vector<int>> to(n);
    rep(i, n-1) {
        int a, b;
        cin >> a >> b;
        --a; --b;
        to[a].push_back(b);
        to[b].push_back(a);
    }

    int ans = 0;
    auto dfs = [&](auto f, int v, int p=-1) -> int {
        int mx1 = 0, mx2 = 0;
        for (int u : to[v]) {
            if (u == p) continue;
            int t = f(f, u, v) + 1;
            if (mx1 < t) {
                mx2 = mx1;
                mx1 = t;
            }
            else if (mx2 < t) {
                mx2 = t;
            }
        }
        chmax(ans, mx1 + mx2);
        return mx1;
    };

    dfs(dfs, 0);

    cout << ans << '\n';

    return 0;
}

4. 树上距离 Ⅰ

给你一颗包含 $n$ 个点的树
你的任务是求出每个顶点到其他点的最远距离。

限制：

• $1 \leqslant n \leqslant 2 \times 10^5$
• $1 \leqslant a, b \leqslant n$

算法分析

我们可以先求出直径 $(a, b)$，对于树上每点来说，到直径两端点中其中一点可做到距离最远。

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using std::cin;
using std::cout;
using std::max;
using std::vector;
using P = std::pair<int, int>;

int main() {
    int n;
    cin >> n;

    vector<vector<int>> to(n);
    rep(i, n-1) {
        int a, b;
        cin >> a >> b;
        --a; --b;
        to[a].push_back(b);
        to[b].push_back(a);
    }

    auto dfs = [&](auto f, int v, int d=0, int p=-1) -> P {
        P res(d, v); 
        if (p == -1) res = P(0, -1);
        for (int u : to[v]) {
            if (u == p) continue;
            res = max(res, f(f, u, d+1, v));
        }
        return res;
    };

    int a = dfs(dfs, 0).second;
    int b = dfs(dfs, a).second;

    vector<int> ans(n);
    auto dfs2 = [&](auto& f, int v, int d=0, int p=-1) -> void {
        if (p != -1) ans[v] = max(ans[v], d);
        for (int u: to[v]) {
            if (u == p) continue;
            f(f, u, d+1, v);
        }
    };

    dfs2(dfs2, a);
    dfs2(dfs2, b);

    rep(i, n) cout << ans[i] << ' ';

    return 0;
}

5. 树上距离 Ⅱ

给你一颗包含 $n$ 个点的树
你的任务是求出每个顶点到其他点的距离总和。

限制：

• $1 \leqslant n \leqslant 2 \times 10^5$
• $1 \leqslant a, b \leqslant n$

算法分析

假设这颗树以顶点 $a$ 为根，顶点 $b$ 为 $a$ 的子节点，如果我们把根换成顶点 $b$ 的话，我们可以发现：

• 以顶点 $b$ 为根的子树中所有点的深度将会 -1
• 除去这颗子树以外的所有点的深度将会 +1

所以我们仅需要使用 $n$ 和以顶点 $b$ 为根的子树大小从而通过顶点 $a$ 的答案转移到顶点 $b$，即 $$ans[b] = ans[a] + (n - siz[b]) - siz[b]$$

双倍经验：树的最长路

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using std::cin;
using std::cout;
using std::vector;
using ll = long long;

int main() {
    int n;
    cin >> n;

    vector<vector<int>> to(n);
    rep(i, n-1) {
        int a, b;
        cin >> a >> b;
        --a; --b;
        to[a].push_back(b);
        to[b].push_back(a);
    }

    vector<int> siz(n);
    auto dfs = [&](auto& f, int v, int p=-1) -> ll {
        ll res = 0;
        siz[v] = 1;
        for (int u : to[v]) {
            if (u == p) continue;
            res += f(f, u, v) + siz[u];
            siz[v] += siz[u]; 
        }
        return res;
    };

    vector<ll> ans(n);
    ans[0] = dfs(dfs, 0);
    auto dfs2 = [&](auto& f, int v, int p=-1) -> void {
        for (int u : to[v]) {
            if (u == p) continue;
            ans[u] = ans[v] + (n - siz[u]) - siz[u];
            f(f, u, v);
        }
    };

    dfs2(dfs2, 0);

    rep(i, n) cout << ans[i] << ' ';

    return 0;
}

6. 公司查询 Ⅰ

一个公司有 $n$ 个员工，他们形成了一个树状层次结构，除了总经理以外，每个员工都有一个直接老板
你的任务是处理 $q$ 个询问：员工 $x$ 的第 $k$ 级老板是谁？
这里的员工 $1$ 为总经理，员工 $i$ 的直接老板为 $e_i \ (2 \leqslant n)$

限制：

• $1 \leqslant n, q \leqslant 2 \times 10^5$
• $1 \leqslant e_i \leqslant i-1$
• $1 \leqslant x \leqslant n$
• $1 \leqslant k \leqslant n$

算法分析

本题其实就是求每个点的第 $k$ 级祖先。考虑对每个点采用倍增，那么从每个点开始将以 $O(\log (n))$ 的时间跳到他的第 $k$ 级祖先

记 anc[v][i] 表示顶点 $v$ 的 $2^j$ 级祖先

$anc[v][i] = anc[anc[v][i-1]][i-1]$

从顶点 $v$ 向上跳 $2^{i-1}$ 步，然后在这个点上再往上跳 $2^{i - 1}$ 步就能到达顶点 $v$ 的第 $2^i$ 级祖先

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using std::cin;
using std::cout;

const int MX = 200005;
int anc[MX][20];

int main() {
    int n, q;
    cin >> n >> q;

    for (int v = 2; v <= n; ++v) cin >> anc[v][0];

    rep(i, 19) {
        for (int v = 1; v <= n; ++v) {
            anc[v][i+1] = anc[anc[v][i]][i];
        }
    }

    rep(qi, q) {
        int x, k;
        cin >> x >> k;
        rep(i, 20) {
            if (k>>i & 1) x = anc[x][i]; 
        }
        cout << (x == 0 ? -1 : x) << '\n';
    }

    return 0;
}

7. 公司查询 Ⅱ

一个公司有 $n$ 个员工，他们形成了一个树状层次结构，除了总经理以外，每个员工都有一个直接上司
你的任务是处理以下 $q$ 个询问：

在整个雇佣关系中，谁是员工 $a$ 和员工 $b$ 共有的级别最低的上司？

这里的员工 $1$ 为总经理，员工 $i$ 的直接上司为 $e_i \ (2 \leqslant n)$

限制：

• $1 \leqslant n, q \leqslant 2 \times 10^5$
• $1 \leqslant e_i \leqslant i-1$
• $1 \leqslant a, b \leqslant n$

算法分析

其实就是求树上任意两点的最近公共祖先
套一下 $\rm LCA$ 的板子即可

C++代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using std::cin;
using std::cout;
using std::vector;

struct LCA {
    int n, bi;
    vector<int> dep;
    vector<vector<int>> to, anc;
    LCA(int n): n(n), dep(n), to(n) {}

    void addEdge(int a, int b) {
        to[a].push_back(b);
        to[b].push_back(a);
    }

    void init(int root = 0) {
        bi = 0;
        while (1<<bi <= n) ++bi;
        anc = vector(n, vector<int>(bi, -1));
        dfs(root);
        rep(i, bi - 1)rep(j, n) anc[j][i + 1] = (anc[j][i] == -1 ? -1 : anc[anc[j][i]][i]);
    }

    void dfs(int v, int p = -1) { 
        dep[v] = dep[p] + 1;
        anc[v][0] = p;
        for (int u : to[v]) {
            if (u == p) continue;
            dfs(u, v);
        }
    }

    int lca(int x, int y) {
        if (dep[x] < dep[y]) std::swap(x, y);
        int d = dep[x] - dep[y];
        for (int i = bi - 1; i >= 0; --i) {
            if (1<<i <= d) x = anc[x][i], d -= 1<<i; 
        }
        if (x == y) return x;
        for (int i = bi - 1; i >= 0; --i) {
            if (anc[x][i] != anc[y][i]) x = anc[x][i], y = anc[y][i];
        }
        return anc[x][0];
    }

    int dist(int x, int y) {
        return dep[x] + dep[y] - 2 * dep[lca(x, y)];
    }
};

int main() {
    int n, q;
    cin >> n >> q;

    LCA g(n);
    for (int i = 1; i < n; ++i) {
        int e;
        cin >> e;
        --e;
        g.addEdge(i, e);
    }

    g.init();

    rep(qi, q) {
        int a, b;
        cin >> a >> b;
        --a; --b;
        int ans = g.lca(a, b) + 1;
        cout << ans << '\n';
    }

    return 0;
}

8. 距离查询

给你一颗包含 $n$ 个节点的树
你的任务是处理以下 $q$ 个询问：

• 点 $a$ 和 点 $b$ 之间的距离是多少？

限制：

• $1 \leqslant n, q \leqslant 2 \times 10^5$
• $1 \leqslant a, b \leqslant n$

算法分析

$dist(a, b) = dep[a] + dep[b] - 2 * dep[lca(a, b)]$

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using std::cin;
using std::cout;
using std::vector;

struct LCA {
    int n, bi;
    vector<int> dep;
    vector<vector<int>> to, anc;
    LCA(int n): n(n), dep(n), to(n) {}

    void addEdge(int a, int b) {
        to[a].push_back(b);
        to[b].push_back(a);
    }

    void init(int root = 0) {
        bi = 0;
        while (1<<bi <= n) ++bi;
        anc = vector(n, vector<int>(bi, -1));
        dfs(root);
        rep(i, bi - 1)rep(j, n) anc[j][i + 1] = (anc[j][i] == -1 ? -1 : anc[anc[j][i]][i]);
    }

    void dfs(int v, int p = -1) { 
        dep[v] = dep[p] + 1;
        anc[v][0] = p;
        for (int u : to[v]) {
            if (u == p) continue;
            dfs(u, v);
        }
    }

    int lca(int x, int y) {
        if (dep[x] < dep[y]) std::swap(x, y);
        int d = dep[x] - dep[y];
        for (int i = bi - 1; i >= 0; --i) {
            if (1<<i <= d) x = anc[x][i], d -= 1<<i; 
        }
        if (x == y) return x;
        for (int i = bi - 1; i >= 0; --i) {
            if (anc[x][i] != anc[y][i]) x = anc[x][i], y = anc[y][i];
        }
        return anc[x][0];
    }

    int dist(int x, int y) {
        return dep[x] + dep[y] - 2 * dep[lca(x, y)];
    }
};

int main() {
    std::ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int n, q;
    cin >> n >> q;

    LCA g(n);
    rep(i, n-1) {
        int a, b;
        cin >> a >> b;
        --a; --b;
        g.addEdge(a, b);
    }

    g.init();

    rep(qi, q) {
        int a, b;
        cin >> a >> b;
        --a; --b;
        int ans = g.dist(a, b);
        cout << ans << '\n';
    }

    return 0;
}

9. 路径统计

给你一颗包含 $n$ 个顶点的树，且这颗树上有 $m$ 条路径。
你的任务是为每个顶点计算包含它的路径数。

限制：

• $1 \leqslant n, q \leqslant 2 \times 10^5$
• $1 \leqslant a, b \leqslant n$

算法分析

暴力的话，对于每条路径上最坏有 $O(n)$ 规模的点，$O(n * q)$ 显然过不去

下面考虑优化：

我们可以开一个差分数组 $d$，对于路径 $a\longleftrightarrow b$，我们可以分别在点 $a$ 处和点 $b$ 处都打一个 +1 的记号，然后在 ${\rm lca}(a, b)$ 的父节点处打一个 -1 的记号，形式上，就是 d[a] += 1, d[b] += 1, d[lca(a, b)] -= 1。
注意到在顶点 ${\rm lca}(a, b)$ 处多加了一个 +1 的记号，所以需要在这个点处加上 -1 的记号
最后把每个点的记号自底向上更新

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using std::cin;
using std::cout;
using std::vector;

const int MX = 200005;
int anc[MX][20], dep[MX], d[MX];
vector<int> to[MX];

void dfs(int v, int p=0) {
    for (int u : to[v]) {
        if (u == p) continue;
        anc[u][0] = v;
        dep[u] = dep[v] + 1;
        dfs(u, v);
    }
}

int lca(int x, int y) {
    if (dep[x] < dep[y]) std::swap(x, y);
    int d = dep[x] - dep[y];
    rep(i, 20) {
        if (d>>i & 1) x = anc[x][i];
    }
    if (x == y) return x;
    for (int i = 19; i >= 0; --i) {
        if (anc[x][i] != anc[y][i]) {
            x = anc[x][i];
            y = anc[y][i];
        }
    }
    return anc[x][0];
}

void dfs2(int v, int p=0) {
    for (int u : to[v]) {
        if (u == p) continue;
        dfs2(u, v);
        d[v] += d[u];
    }
}

int main() {
    int n, m;
    cin >> n >> m;

    rep(i, n-1) {
        int a, b;
        cin >> a >> b;
        to[a].push_back(b);
        to[b].push_back(a);
    }

    dfs(1);

    for (int i = 1; i < 20; ++i) {
        for (int j = 1; j <= n; ++j) {
            anc[j][i] = anc[anc[j][i-1]][i-1];
        }
    }

    rep(mi, m) {
        int a, b;
        cin >> a >> b;
        d[a]++;
        d[b]++;
        d[anc[lca(a, b)][0]]--;
        d[lca(a, b)]--;
    }

    dfs2(1);

    for (int i = 1; i <= n; ++i) {
        cout << d[i] << " ";
    }

    return 0;
}

10. 子树查询

给你一颗包含 $n$ 个顶点的有根树。顶点编号分别为 $1, 2, \cdots, n$，且以顶点 $1$ 为根。每个顶点都有一个点权。

你的任务是处理以下询问：

1. 把顶点 $x$ 的点权改为 $x$
2. 计算以顶点 $s$ 为根的子树上的点权之和

算法分析

由于以点 $x$ 为根的子树的 dfs序 是连续的一段，所以只需要维护一个 $\rm dfs$ 序，用树状数组实现：单点修改和区间查询

这里开两个数组 in 和 out 分别表示进入点 $v$ 的时间，以及扫描完点 $v$ 的子树后离开这点的时间

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using std::cin;
using std::cout;
using std::vector;
using ll = long long;

template<typename T>
struct BIT {
  int n;
  vector<T> d;
  BIT(int n=0):n(n),d(n+1) {}
  void add(int i, T x=1) {
    for (i++; i <= n; i += i&-i) {
      d[i] += x;
    }
  }
  T sum(int i) {
    T x = 0;
    for (i++; i; i -= i&-i) {
      x += d[i];
    }
    return x;
  }
  T sum(int l, int r) {
    return sum(r-1) - sum(l-1);
  }
};

int main() {
    int n, q;
    cin >> n >> q;

    vector<int> a(n);
    rep(i, n) cin >> a[i];

    vector<vector<int>> to(n);
    rep(i, n-1) {
        int a, b;
        cin >> a >> b;
        --a; --b;
        to[a].push_back(b);
        to[b].push_back(a);
    } 

    int idx = 0;
    vector<int> in(n), out(n);
    auto dfs = [&](auto f, int v, int p=-1) -> void {
        in[v] = idx++;
        for (int u : to[v]) {
            if (u == p) continue;
            f(f, u, v);
        }
        out[v] = idx;
    };

    dfs(dfs, 0);

    BIT<ll> t(n);
    rep(i, n) t.add(in[i], a[i]);

    rep(qi, q) {
        int type, s;
        cin >> type >> s;
        --s;
        if (type == 1) {
            int x;
            cin >> x;
            t.add(in[s], x - a[s]); // 把 in[s] 处的 d 值改为 x 
            a[s] = x;
        }
        else {
            cout << t.sum(in[s], out[s]) << '\n';
        }
    }

    return 0;
}

11. 路径查询 Ⅰ

给你一颗包含 $n$ 个顶点的有根树。顶点编号分别为 $1, 2, \cdots, n$，且以顶点 $1$ 为根。每个顶点都有一个点权。

你的任务是处理以下询问：

• 把点 $s$ 的点权改为 $x$
• 计算从根节点到点 $s$ 这条路径上的点权之和

限制：

• $1 \leqslant n, q \leqslant 2 \times 10^5$
• $1 \leqslant a, b, s \leqslant n$
• $1 \leqslant v_i, x \leqslant 10^9$

算法分析

和上题一样，只需维护一个 dfs序，依然可以用树状数组实现
注意到，把点 $s$ 的点权更新成 $x$ 之时，那么从根节点到以点 $s$ 为根的子树上的每个点的路径上的点权和会相应增加 $x - a[s]$
最后的答案只需求下标 $in[s]$ 处的前缀和即可

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 1; i <= (n); ++i)

using std::cin;
using std::cout;
using std::vector;
using ll = long long;

template<typename T>
struct BIT {
  int n;
  vector<T> d;
  BIT(int n=0):n(n),d(n+1) {}
  void add(int i, T x=1) {
    for (i++; i <= n; i += i&-i) {
      d[i] += x;
    }
  }
  T sum(int i) {
    T x = 0;
    for (i++; i; i -= i&-i) {
      x += d[i];
    }
    return x;
  }
  T sum(int l, int r) {
    return sum(r-1) - sum(l-1);
  }
};

int main() {
    int n, q;
    cin >> n >> q;

    vector<int> a(n+1);
    rep(i, n) cin >> a[i];

    vector<vector<int>> to(n+1);
    rep(i, n-1) {
        int u, v;
        cin >> u >> v;
        to[u].push_back(v);
        to[v].push_back(u);
    }

    int idx = 0;
    vector<int> in(n+1), out(n+1);
    auto dfs = [&](auto f, int v, int p=0) -> void {
        in[v] = ++idx;
        for (int u : to[v]) {
            if (u == p) continue;
            f(f, u, v);
        }
        out[v] = idx;
    };

    dfs(dfs, 1);

    BIT<ll> t(n+1);
    rep(i, n) {
        t.add(in[i], a[i]);
        t.add(out[i]+1, -a[i]); // 消除上面操作的影响 
    }

    rep(qi, q) {
        int type, s;
        cin >> type >> s;
        if (type == 1) {
            int x;
            cin >> x;
            t.add(in[s], x-a[s]);
            t.add(out[s]+1, -(x-a[s])); // 消除上面操作的影响 
            a[s] = x;
        }
        else {
            cout << t.sum(in[s]) << '\n';
        } 
    }

    return 0;
}

12. 路径查询 Ⅱ

给你一颗包含 $n$ 个顶点的有根树。顶点编号分别为 $1, 2, \cdots, n$，且以顶点 $1$ 为根。每个顶点都有一个点权。

你的任务是处理以下询问：

• 把点 $s$ 的点权改为 $x$
• 计算点 $a$ 和点 $b$ 这条路径上的点权的最大值

限制：

• $1 \leqslant n, q \leqslant 2 \times 10^5$
• $1 \leqslant a, b, s \leqslant n$
• $1 \leqslant v_i, x \leqslant 10^9$

算法分析

这里用树剖来实现会比较方便

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 1; i <= (n); ++i)

using std::cin;
using std::cout;
using std::max;
using std::vector;
using ll = long long;

const int MX = 100005;
vector<int> to[MX];
int n;
int a[MX], w[MX];
int dep[MX], fa[MX], hson[MX], siz[MX];

void dfs1(int v) {
    siz[v] = 1;

    for (int u : to[v]) {
        if (u == fa[v]) continue;
        dep[u] = dep[v] + 1;
        fa[u] = v;
        dfs1(u);
        siz[v] += siz[u];

        if (siz[u] > siz[hson[v]]) {
            hson[v] = u;
        } 
    }
}

int pre[MX], idx;
int rnk[MX];
int top[MX];

void dfs2(int v, int x) {
    pre[v] = ++idx;
    w[idx] = a[v];
    rnk[idx] = v;
    top[v] = x;

    if (!hson[v]) return;
    dfs2(hson[v], x);

    for (int u : to[v]) {
        if (u == fa[v] or u == hson[v]) continue;
        dfs2(u, u);
    }
}

int mx[MX * 4];

inline int lc(int p) { return p << 1; }

inline int rc(int p) { return p << 1 | 1; }

void pushUp(int p) {
    mx[p] = max(mx[lc(p)], mx[rc(p)]);
}


void buildTree(int p, int l, int r) {
    if (l == r) {
        mx[p] = w[l];
        return;
    }
    int mid = (l + r) >> 1;
    buildTree(lc(p), l, mid);
    buildTree(rc(p), mid + 1, r);
    pushUp(p);
}

void update(int p, int l, int r, int q, int d) {
    if (l == r) { 
        mx[p] = d;
        return;
    }

    int mid = (l + r) >> 1;
    if (q <= mid) {
        update(lc(p), l, mid, q, d);
    } 
    if (mid < q) {
        update(rc(p), mid + 1, r, q, d);
    }
    pushUp(p);
}

int query(int p, int l, int r, int ql, int qr) {
    if (ql <= l && r <= qr) return mx[p];

    int mid = (l + r) >> 1;
    int res = 0;
    if (ql <= mid) {
        res = max(res, query(lc(p), l, mid, ql, qr));
    }
    if (mid < qr) {
        res = max(res, query(rc(p), mid + 1, r, ql, qr));
    }
    return res;
}

int qPath(int u, int v) {
    int ans = 0;
    while (top[u] != top[v]) {
        if (dep[top[u]] < dep[top[v]]) std::swap(u, v);
        ans = max(ans, query(1, 1, n, pre[top[u]], pre[u]));
        u = fa[top[u]];
    }

    if (dep[u] > dep[v]) std::swap(u, v);
    ans = max(ans, query(1, 1, n, pre[u], pre[v]));
    return ans;
}

int main() {
    int m;
    cin >> n >> m;
    rep(i, n) cin >> a[i];
    rep(i, n-1) {
        int x, y;
        cin >> x >> y;
        to[x].push_back(y);
        to[y].push_back(x);
    }

    dfs1(1);
    dfs2(1, 1);

    buildTree(1, 1, n);

    while (m--) {
        int type;
        cin >> type;
        if (type == 1) {
            int s, x;
            cin >> s >> x;
            update(1, 1, n, pre[s], x);
        }
        else {
            int a, b;
            cin >> a >> b;
            cout << qPath(a, b) << '\n';
        }
    }

    return 0;
}

13. 不同的颜色

给你一颗含有 $n$ 个节点的有根树。节点的编号分别为 $1, 2, \cdots, n$，且以节点 $1$ 为根。每个点都有一个颜色 $c_i$

对于每个点 $1, 2, \cdots, n$，输出以该点为根的子树中有多少种不同的颜色。

限制：

• $1 \leqslant n \leqslant 2 \times 10^5$
• $1 \leqslant a, b \leqslant n$
• $1 \leqslant c_i \leqslant 10^9$

算法分析

对于每个点，可以用一个集合来维护这个点的颜色，我们希望将每个点的子树中的集合合并在一起，这样每个点就有一个由以这个点为根的子树中的所有颜色构成的集合

如何合并两个集合？

暴力做法：

假设集合 $a$ 的大小为 $n$，集合 $b$ 的大小为 $m$，可以按以下方式将两个集合合并：

for (int x : b) a.insert(x);

时间复杂度是 $O(m\log (n+m))$，总复杂度是 $N^2 \log N$

更好的做法：

只需在上面加一行如下的代码就能加速：

if (a.size() < b.size()) swap(a, b)

注意到 swap 可以以 $O(1)$ 的时间交换两个集合。所以，将更小的集合 $b$ 合并到更大的集合 $a$ 只需要 $O(m\log n)$ 的时间，总的时间复杂度为 $O(N \log^2 N)$

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using std::cin;
using std::cout;
using std::set;
using std::vector;

const int MX = 200005;

vector<int> to[MX];
set<int> colors[MX];
int distinct_num[MX];

void dfs(int v, int p=-1) {
    for (int u : to[v]) {
        if (u == p) continue;
        dfs(u, v);
        if (colors[v].size() < colors[u].size()) {
            swap(colors[v], colors[u]);
        }
        for (int c : colors[u]) {
            colors[v].insert(c);
        }
    }
    distinct_num[v] = colors[v].size();
}

int main() {
    cin.tie(nullptr) -> sync_with_stdio(false);

    int n;
    cin >> n;

    rep(i, n) {
        int c;
        cin >> c;
        colors[i].insert(c);
    }

    rep(i, n-1) {
        int a, b;
        cin >> a >> b;
        --a; --b;
        to[a].push_back(b);
        to[b].push_back(a);
    }

    dfs(0);

    rep(i, n) {
        cout << distinct_num[i] << '\n';
    }

    return 0;
}

14. Finding a Centroid

给你一颗含有 $n$ 个节点的树，要求找到树的重心，也就是将根节点换成这个点时，每颗子树上至多有 $\lfloor\frac{n}{2}\rfloor$ 个点

限制：

• $1 \leqslant n \leqslant 2 \times 10^5$

算法分析

从根节点开始，遍历它的每个子树，如果它的所有子树大小都不超过 $\lfloor\frac{n}{2}\rfloor$ 的话，那么这个点就是重心。否则，就将根节点换到子树大小超过 $\lfloor\frac{n}{2}\rfloor$ 的那个子节点上，并重复之前的操作，直到找到重心。

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using std::cin;
using std::cout;
using std::vector;

const int MX = 200005;

int n;
vector<int> to[MX];

int sz[MX];
void tfs(int v, int p=-1) {
    sz[v] = 1;
    for (int u : to[v]) {
        if (u == p) continue;
        tfs(u, v);
        sz[v] += sz[u]; 
    }
}

int get_centroid(int v, int p=-1) {
    for (int u : to[v]) {
        if (u == p) continue;
        if (sz[u]*2 > n) {
            return get_centroid(u, v);
        }
    }
    return v;
}

int main() {
    cin >> n;

    rep(i, n-1) {
        int a, b;
        cin >> a >> b;
        --a; --b;
        to[a].push_back(b);
        to[b].push_back(a);
    }

    tfs(0);

    int centroid = get_centroid(0) + 1;
    cout << centroid << '\n';

    return 0;
}

15. Fixed-Length Paths I

给定一颗含有 $N$ 颗节点的树，要求恰经过 $k$ 条边的不同路径数。

限制：

• $1 \leqslant k \leqslant n \leqslant 2 \times 10^5$

算法分析

点分治板题

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;
using ll = long long;

const int MX = 200005;

int n, k;
vector<int> to[MX];
bool used[MX];

int sz[MX];
int tfs(int v, int p=0) {
    sz[v] = 1;
    for (int u : to[v]) {
        if (used[u] or u == p) continue;
        sz[v] += tfs(u, v);
    }
    return sz[v];
}

int get_centroid(int desired, int v, int p=0) {
    for (int u : to[v]) {
        if (used[u] or u == p) continue;
        if (sz[u] >= desired) {
            return get_centroid(desired, u, v);
        }
    }
    return v;
}

ll ans = 0;
int cnt[MX]{1}, mx_d;
void get_cnt(int v, int p, bool filling, int d=1) {
    if (d > k) return;
    mx_d = max(mx_d, d);
    if (filling) cnt[d]++;
    else ans += cnt[k-d];
    for (int u : to[v]) {
        if (used[u] or u == p) continue;
        get_cnt(u, v, filling, d+1);
    }
}

void centroid_decomp(int v) {
    int centroid = get_centroid(tfs(v)/2, v);
    used[centroid] = true;
    mx_d = 0;
    for (int u : to[centroid]) {
        if (used[u]) continue;
        get_cnt(u, centroid, false);
        get_cnt(u, centroid, true);
    }
    fill(cnt+1, cnt+mx_d+1, 0);
    for (int u : to[centroid]) if (!used[u]) centroid_decomp(u);
}

int main() {
    cin.tie(nullptr) -> sync_with_stdio(false);

    cin >> n >> k;
    rep(i, n-1) {
        int a, b;
        cin >> a >> b;
        to[a].push_back(b);
        to[b].push_back(a);
    }

    centroid_decomp(1);

    cout << ans << '\n';

    return 0;
}

17. Tree Traversals

有三种方式遍历一颗二叉树：前序遍历、中序遍历和后序遍历

有一个 $n$ 个节点的二叉树，节点编号各不相同。给你这颗树的前序遍历和中序遍历，请确定它的后序遍历

限制：

• $1 \leqslant n \leqslant 10^5$

算法分析

板题

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using std::cin;
using std::cout;
using std::vector;

int main() {
    int n;
    cin >> n;

    vector<int> pre(n), in(n);
    rep(i, n) cin >> pre[i], pre[i]--;
    rep(i, n) cin >> in[i], in[i]--;

    vector<int> ni(n);
    rep(i, n) ni[in[i]] = i;
    vector<int> l(n), r(n);
    vector<int> post;
    auto f = [&](auto& f, int lp, int li, int n) -> void {
        if (n == 0) return;
        int root = pre[lp];
        int i = ni[root];
        int ls = i-li, rs = n-1-ls;
        f(f, lp+1, li, ls);
        f(f, lp+1+ls, li+ls+1, rs);
        post.push_back(root+1);
    };

    f(f, 0, 0, n);

    for (int x : post) {
        cout << x << ' ';
    }

    return 0;
}

19. Tree Distance（★5）

给定一个具有 $N$ 个顶点的树。树的顶点编号分别为 $1 \sim N$ 。
对于第 $i$ 条边，顶点 $a_i$ 和顶点 $b_i$ 相互连通，边权为 $1$ 。

求 $\displaystyle \sum_{u=1}^N\sum_{v=u+1}^N \operatorname{dist}(u, v)$

这里，$\operatorname{dist}(u, v)$ 为顶点 $u$ 到顶点 $v$ 的最短距离。

限制：

• $2 \leqslant N \leqslant 10^5$

算法分析

考虑每条边对答案的贡献
比如下图中，含有边 $(1, 5)$ 的顶点对有 $(1, 3), \ (1, 4), \ (1, 5), \ (2, 3), \ (2, 4), \ (2, 5)$ 这 $6$ 对

记下图中以紫色点为根的子树记作 $A$，其余点构成的图记作 $B$，那么红色边的对答案的贡献就是 $|A| \times |B| = |A| \times (N-|A|)$

接下来只需求出以每个点为根的子树大小即可

C++ 代码

#include <bits/extc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using std::cin;
using std::cout;
using std::vector;
using ll = long long;

int main() {
    int n;
    cin >> n;

    vector<vector<int>> to(n);
    rep(i, n - 1) {
        int a, b;
        cin >> a >> b;
        --a; --b;
        to[a].push_back(b);
        to[b].push_back(a);
    }

    ll ans = 0;
    vector<int> t(n);
    auto dfs = [&](auto& f, int v, int p = -1) -> void {
        t[v] = 1;
        for (int u : to[v]) {
            if (u == p) continue;
            f(f, u, v);
            ans += (ll)t[u]*(n-t[u]);
            t[v] += t[u];
        }
    };
    dfs(dfs, 0);

    cout << ans << '\n';

    return 0;
}

20. Distance Sums 2

给定一个有 $N$ 个顶点的树。这些点的编号分别为 $1, 2, \cdots, N$，第 $i$ 条边是一条连接点 $u_i$ 和 $v_i$ 的无向边。

对于每个整数 $i(1 \leqslant i \leqslant N)$，求 $\sum\limits_{j=1}^N dis(i, j)$

其中，dis(i, j) 表示从点 $i$ 遍历到点 $j$ 的最短距离。

限制：

• $2 \leqslant N \leqslant 2 \times 10^5$
• $2 \leqslant u_i < v_i \leqslant N$

算法分析

记 Ans[v] 为点 $v$ 的答案，sz[v] 表示以点 $v$ 为根的子树大小

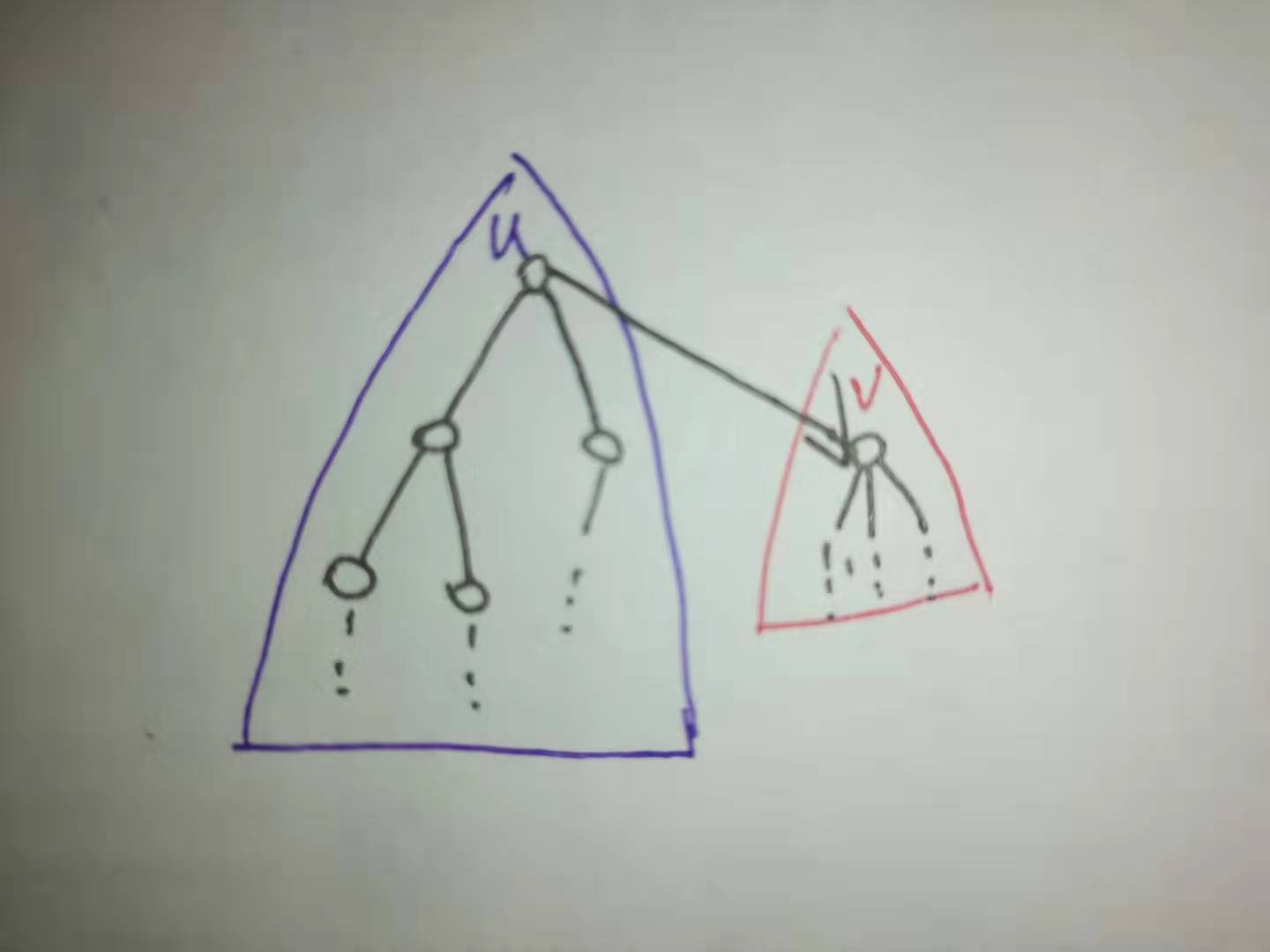
假设一开始以点 $u$ 为根，现在我们把点 $v$ 换到根的位置，$u$ 变为其孩子节点，这样此时以点 $u$ 为根的子树中的所有点对点 $v$ 的贡献将增加 $1$，而原先以点 $u$ 为根的子树中的所有点对 $u$ 的贡献将减少 $1$。于是

$$ Ans[v] = Ans[u] + (n - sz[u]) - sz[u] $$

C++ 代码

#pragma GCC target("avx2")
#pragma GCC optimize("O3")
#pragma GCC optimize("unroll-loops")
#pragma GCC optimize("Ofast")
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using std::cin;
using std::cout;
using std::vector;
using ll = long long;

int main() {
    int n;
    cin >> n;

    vector<vector<int>> to(n);
    rep(i, n - 1) {
        int a, b;
        cin >> a >> b;
        --a; --b;
        to[a].push_back(b);
        to[b].push_back(a);
    }

    vector<int> t(n);
    vector<ll> ans(n);
    auto dfs1 = [&](auto& f, int v, int p = -1) -> ll {
        ll res = 0;
        t[v] = 1;
        for (int u : to[v]) {
            if (u == p) continue;
            res += f(f, u, v) + t[u];
            t[v] += t[u];
        }
        return res;
    };
    ans[0] = dfs1(dfs1, 0);
    auto dfs2 = [&](auto& f, int v, int p = -1) -> void {
        for (int u : to[v]) {
            if (u == p) continue;
            ans[u] = ans[v] + (n - t[u]) - t[u];
            f(f, u, v);
        }
    };
    dfs2(dfs2, 0);

    rep(i, n) cout << ans[i] << '\n';

    return 0;
}

21. 小猴摘桃

给定一颗树，求树上经过偶数个节点的路径数量。

限制：

• $n \leqslant 10^5$

参考难度：

普及+/提高

算法分析

树形dp

记 dp[v][0/1] 表示以 $v$ 为根的子树中到 $v$ 距离为偶数/奇数的点的个数

转移方程：

dp[v][0] += dp[u][1]
dp[v][1] += dp[u][0]+1

最后的答案就是 $(dp[1][0]+1) \times dp[1][1]$ 。

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;
using ll = long long;

int main() {
    int n;
    cin >> n;

    vector<vector<int>> to(n);
    rep(i, n-1) {
        int a, b;
        cin >> a >> b;
        --a; --b;
        to[a].push_back(b);
        to[b].push_back(a);
    }

    vector<vector<int>> dp(n, vector<int>(2));
    auto dfs = [&](auto& f, int v, int p=-1) -> void {
        for (int u : to[v]) {
            if (u == p) continue;
            f(f, u, v);
            dp[v][0] += dp[u][1];
            dp[v][1] += dp[u][0]+1;
        }
    };
    dfs(dfs, 0);

    ll ans = (ll)(dp[0][0]+1) * dp[0][1];
    cout << ans << '\n';

    return 0;
}

22. 树上归零

给定一棵有 $n$ 个结点的树，$1$ 号点为根。树上每个点都有一个值，其中第 $i$ 个点的值为 $a_i$。小爱想通过若干步操作将树上的所有值全部变为 $0$，每步操作可以选择树上任意一个结点 $u$，然后将 $u$ 的子树上的所有值增加 $1$，或者将 $u$ 的子树上的所有值减少 $1$。

请问小爱最少需要几步操作才能将树上所有点的数值变成 $0$？

限制：

• $1 \leqslant n \leqslant 10^5$
• $|a_i| \leqslant 10^9$

算法分析

从叶子节点开始自底向上求出每个点（除根节点）的点权变成其父节点的点权所需的操作次数（若对点 $v$ 做清零操作，会令其子节点 $u$ 的点权的绝对值变为 $|A_v - A_u|$）
对于根节点，直接将该点点权的绝对值加入答案即可

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;
using ll = long long;

int main() {
    int n;
    cin >> n;

    vector<vector<int>> to(n);
    for (int i = 1; i < n; ++i) {
        int p;
        cin >> p;
        --p;
        to[p].push_back(i);
    }

    vector<int> a(n);
    rep(i, n) cin >> a[i];

    ll ans = abs(a[0]);
    auto dfs = [&](auto& f, int v, int p=-1) -> void {
        for (int u : to[v]) {
            f(f, u, v);
            ans += abs(a[u]-a[v]);
        }
    };
    dfs(dfs, 0);

    cout << ans << '\n';

    return 0;
}

23. Maximum White Subtree

给定一个 $n$ 个点的树。树是由 $n-1$ 条无向边构成的无向连通图。每个点都分配了一种颜色，如果点 $v$ 是白色，则 $a_v = 1$；如果点 $v$ 是黑色，则 $a_v = 0$。

要求遍历每个点 $v$，选出一个连通子图，令子图中白色点数为 $cnt_w$，以及黑色点数为 $cnt_b$，使得 $cnt_w - cnt_b$ 达到最大，并输出这个最大值。

限制：

• $2 \leqslant n \leqslant 2 \times 10^5$
• $0 \leqslant a_i \leqslant 1$

算法分析

不妨令点 $1$ 为根节点

记 dp[v] 表示在以点 $v$ 为根的子树中白点数和黑点数之间的最大差值

转移方程：

$ dp[v] = (a[v] == 1 ~? ~1 : -1) + \sum\limits_{u \in \operatorname{children}[v]} \max(0, dp[u]) $

然后自底向上 $\operatorname{dfs}$ 整颗树求出所有点的 $dp[v]$

记 ans[v] 表示在包含点 $v$ 的连通块中白点数和黑点数之间的最大差值

当 $v = 1$ 时，$ans[v] = dp[v]$
当 $v \neq 1$ 时，$ans[v] = dp[v] + \max(0, ans[p]-\max(0, dp[v]))$，其中 $p$ 为 $v$ 的父节点

然后自顶向下 $\operatorname{dfs}$ 整颗树求出所有点的 $ans[v]$

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;

int main() {
    cin.tie(nullptr) -> sync_with_stdio(false);

    int n;
    cin >> n;

    vector<int> a(n);
    rep(i, n) cin >> a[i];

    vector<vector<int>> to(n);
    rep(i, n-1) {
        int u, v;
        cin >> u >> v;
        --u; --v;
        to[u].push_back(v);
        to[v].push_back(u);
    }

    vector<int> dp(n);
    auto dfs1 = [&](auto& f, int v, int p=-1) -> void {
        dp[v] = a[v] == 1 ? 1 : -1;
        for (int u : to[v]) {
            if (u == p) continue;
            f(f, u, v);
            dp[v] += max(0, dp[u]);
        }
    };
    dfs1(dfs1, 0);

    vector<int> ans(n);
    auto dfs2 = [&](auto& f, int v, int p=-1) -> void {
        ans[v] = dp[v];
        if (p != -1) ans[v] += max(0, ans[p]-max(0, dp[v]));
        for (int u : to[v]) {
            if (u == p) continue;
            f(f, u, v);
        }
    };
    dfs2(dfs2, 0);

    rep(i, n) cout << ans[i] << ' ';

    return 0;
}

24. 树的独立集

给定一棵拥有 $n$ 个结点的树，$1$ 号点为这棵树的根。请统计，这棵树拥有多少种不同的独立集。

所谓独立集，是一个由树上结点构成的子集，树任意一条边的两个点不能同时在独立集里。空集也是一种独立集。

由于独立集数量可能很大，输出种类数模 $1,000,000,007$ 的余数即可。

限制：

• $1 \leqslant n \leqslant 2 \times 10^5$

算法分析

记 dp[v][0/1] 表示将点 $v$ 染成白色或黑色时以点 $v$ 为根的子树的染色方案数

转移方程：

$ \begin{cases} dp[v][0] = \prod\limits_u (dp[u][0] + dp[u][1])\\\ dp[v][1] = \prod\limits_u dp[u][0] \end{cases} $

其中 $u$ 是 $v$ 的子节点

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;
using ll = long long;

//const int mod = 998244353;
const int mod = 1000000007;
struct mint {
    ll x;
    mint(ll x=0):x((x%mod+mod)%mod) {}
    mint operator-() const {
        return mint(-x);
    }
    mint& operator+=(const mint a) {
        if ((x += a.x) >= mod) x -= mod;
        return *this;
    }
    mint& operator-=(const mint a) {
        if ((x += mod-a.x) >= mod) x -= mod;
        return *this;
    }
    mint& operator*=(const mint a) {
        (x *= a.x) %= mod;
        return *this;
    }
    mint operator+(const mint a) const {
        return mint(*this) += a;
    }
    mint operator-(const mint a) const {
        return mint(*this) -= a;
    }
    mint operator*(const mint a) const {
        return mint(*this) *= a;
    }
    mint pow(ll t) const {
        if (!t) return 1;
        mint a = pow(t>>1);
        a *= a;
        if (t&1) a *= *this;
        return a;
    }

    // for prime mod
    mint inv() const {
        return pow(mod-2);
    }
    mint& operator/=(const mint a) {
        return *this *= a.inv();
    }
    mint operator/(const mint a) const {
        return mint(*this) /= a;
    }
};
istream& operator>>(istream& is, mint& a) {
    return is >> a.x;
}
ostream& operator<<(ostream& os, const mint& a) {
    return os << a.x;
}

int main() {
    int n;
    cin >> n;

    vector<vector<int>> to(n);
    for (int i = 1; i < n; ++i) {
        int p;
        cin >> p;
        --p; 
        to[p].push_back(i);
    }

    vector dp(n, vector<mint>(2));
    auto dfs = [&](auto f, int v, int p=-1) -> void {
        mint a = 1, b = 1;
        for (int u : to[v]) {
            f(f, u, v);
            a *= dp[u][0] + dp[u][1];
            b *= dp[u][0];
        }
        dp[v][0] = a;
        dp[v][1] = b;
    };
    dfs(dfs, 0);

    mint ans = dp[0][0]+dp[0][1];
    cout << ans << '\n';

    return 0;
}

25. 树的最大和

给定一棵 $n$ 个结点的树，$1$ 号点为根。每个点都有一个权值，第 $i$ 个点的权值为 $a_i$，权值有正有负。请在这棵树里找到一个连通分量，该连通分量内结点的权值之和达到最大，输出这个最大和。

连通分量是指树上一些点的集合，如果用树上的边连接这些点不需要经过连通分量外的点。连通分量可以是空集，空集的权值之和定义为 $0$。

限制：

• $1 \leqslant n \leqslant 2 \times 10^5$
• $|a_i| \leqslant 10^9$

算法分析

见 P1122 最大子树和

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;
using ll = long long;

int main() {
    int n;
    cin >> n;

    vector<vector<int>> to(n);
    for (int i = 1; i < n; ++i) {
        int p;
        cin >> p;
        --p;
        to[p].push_back(i);
    }

    vector<int> a(n);
    rep(i, n) cin >> a[i];

    vector<ll> dp(n);
    auto dfs = [&](auto& f, int v, int p=-1) -> void {
        dp[v] = a[v];
        for (int u : to[v]) {
            f(f, u, v);
            dp[v] += max<ll>(0, dp[u]);
        }
    };
    dfs(dfs, 0);

    ll ans = numeric_limits<ll>::max() + 1;
    rep(i, n) ans = max(ans, dp[i]);

    cout << ans << '\n';

    return 0;
}

26. 树的颜色

给定一棵 $n$ 个结点的树，$1$ 号点为根。每个点都有一个颜色，不同点的颜色可能不同，也可能相同。颜色总数不超过 $n$，编号在 $1$ 到 $n$ 之间。第 $i$ 个点的颜色为 $c_i$ 。请为每个点统计，它的子孙后代中（不包括其本身）有多少点的颜色与它相同。

限制：

• $1 \leqslant n \leqslant 2 \times 10^5$
• $1 \leqslant c_i \leqslant n$

算法分析

三种做法：

• 树上启发式合并
• 树上莫队
• 可以用树上 $\operatorname{dfs}$ 来统计区间 $\bigg[\operatorname{in}[1], \operatorname{out}[v]\bigg]$ 中每个点对 点 $v$ 上颜色 $c$ 的贡献，然后将它容斥掉区间 $\bigg[\operatorname{in}[1], \operatorname{in}[v]\bigg]$ 中的点对颜色 $c$ 的贡献，就能求出点 $v$ 的答案。

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;

int main() {
    int n;
    cin >> n;

    vector<vector<int>> to(n);
    for (int i = 1; i < n; ++i) {
        int p;
        cin >> p;
        --p;
        to[p].push_back(i);
    }

    vector<int> c(n);
    rep(i, n) cin >> c[i], c[i]--;

    vector<int> cnt(n), ans(n);
    auto dfs = [&](auto& f, int v) -> void {
        ans[v] = ++cnt[c[v]];
        for (int u : to[v]) {
            f(f, u);
        }
        ans[v] = cnt[c[v]]-ans[v];
    };
    dfs(dfs, 0);

    rep(i, n) cout << ans[i] << ' ';

    return 0;
}

27. 巨大企業

给定一颗 $n$ 个点的树，对于点 $i (1 \leqslant i \leqslant n)$，唯一指向点 $p_i$，特别地，若 $p_i = -1$ 时，点 $i$ 为根节点

现在给定 $q$ 个询问：

• 对于点 $a_i$ 和点 $b_i$，能否从点 $a_i$ 走到点 $b_i$

限制：

• $2 \leqslant n \leqslant 150000$
• $1 \leqslant q \leqslant 100000$
• $1 \leqslant a_i, b_i \leqslant n$
• $a_i \neq b_i$

算法分析

最直接的做法应该是利用 $\operatorname{lca}$，若 $\operatorname{lca}(a_i, b_i) = b_i$，则满足要求
可以用倍增来求 $\operatorname{lca}$

介绍一下更好的做法：

注意到若从点 $a_i$ 能走到点 $b_i$，那么点 $a_i$ 一定在以点 $b_i$ 为根的子树中
所以，我们 可以用 $\operatorname{dfs}$ 序来解决

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;

int main() {
    int n;
    cin >> n;

    vector<vector<int>> to(n);
    int r;
    rep(i, n) {
        int p;
        cin >> p;
        if (p == -1) {
            r = i;
            continue;
        }
        to[p-1].push_back(i);
    }

    vector<int> in(n), out(n);
    int id = 0;
    auto dfs = [&](auto f, int v) -> void {
        in[v] = id++;
        for (int u : to[v]) f(f, u);
        out[v] = id;
    };
    dfs(dfs, r);

    int q;
    cin >> q;
    rep(qi, q) {
        int a, b;
        cin >> a >> b;
        --a; --b;
        if (in[b] <= in[a] and out[a] <= out[b]) puts("Yes");
        else puts("No");
    }

    return 0;
}

28. 筆塗り

给定一颗包含 $N$ 个点的树，树点编号分别为 $1 \sim N$。这颗树有 $N-1$ 条树边，编号分别为 $1 \sim N-1$，其中第 $i$ 条无向边连接点 $a_i$ 和点 $b_i$。现在要对每条树边进行染色，颜色用 $0 \sim 10^5$ 之间的一个整数来表示。一开始，每条边被染成颜色 $0$。

接下来对这颗树进行 $Q$ 个操作：

• 对于第 $i$ 个操作，将从点 $u_i$ 到点 $v_i$ 的树链上的每条树边染成颜色 $c_i$

检查在 $Q$ 次操作后每条边的颜色。

限制：

• $2 \leqslant N \leqslant 10^5$
• $1 \leqslant Q \leqslant 10^5$
• $1 \leqslant a_i, b_i, u_i, v_i \leqslant N$
• $u_i \neq v_i$
• $1 \leqslant c_i \leqslant 10^5$

算法分析

dsu on tree

C++ 代码

#include <bits/stdc++.h>
#if __has_include(<atcoder/all>)
#include <atcoder/all>
using namespace atcoder;
#endif
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;
using P = pair<int, int>;

int main() {
    int n, q;
    cin >> n >> q;

    vector<vector<P>> g(n);
    rep(i, n-1) {
        int a, b;
        cin >> a >> b;
        --a; --b;
        g[a].emplace_back(b, i);
        g[b].emplace_back(a, i);
    }

    vector<vector<P>> qs(n);
    rep(qi, q) {
        int u, v, c;
        cin >> u >> v >> c;
        --u; --v;
        qs[u].emplace_back(qi, c);
        qs[v].emplace_back(qi, c);
    }

    vector<int> ans(n-1);
    auto dfs = [&](auto f, int v, int p=-1) -> set<P> {
        set<P> s(qs[v].begin(), qs[v].end());
        for (auto [u, i] : g[v]) {
            if (u == p) continue;
            set<P> ns = f(f, u, v);
            if (ns.size()) ans[i] = ns.rbegin()->second;
            if (s.size() < ns.size()) swap(s, ns);
            for (auto p : ns) {
                auto it = s.find(p);
                if (it != s.end()) s.erase(it);
                else s.insert(p);
            }
        }
        return s;
    };
    dfs(dfs, 0);

    rep(i, n-1) cout << ans[i] << '\n';

    return 0;
}

29. Path Intersection

给定一颗 $N$ 个点的树，顶点编号分别为 $1, 2, \cdots, N$，同时给定顶点 $S$ 和 $T$。第 $i$ 条边连接点 $u_i$ 和点 $v_i$。

对于树上每个点 $j$，回答以下询问：

• 求点 $S$ 到点 $j$ 的最短路和点 $T$ 与点 $j$ 的最短路有多少个交点

算法分析

答案为 $\frac{d(S, j) + d(T, j) - d(S, T)}{2} +1$

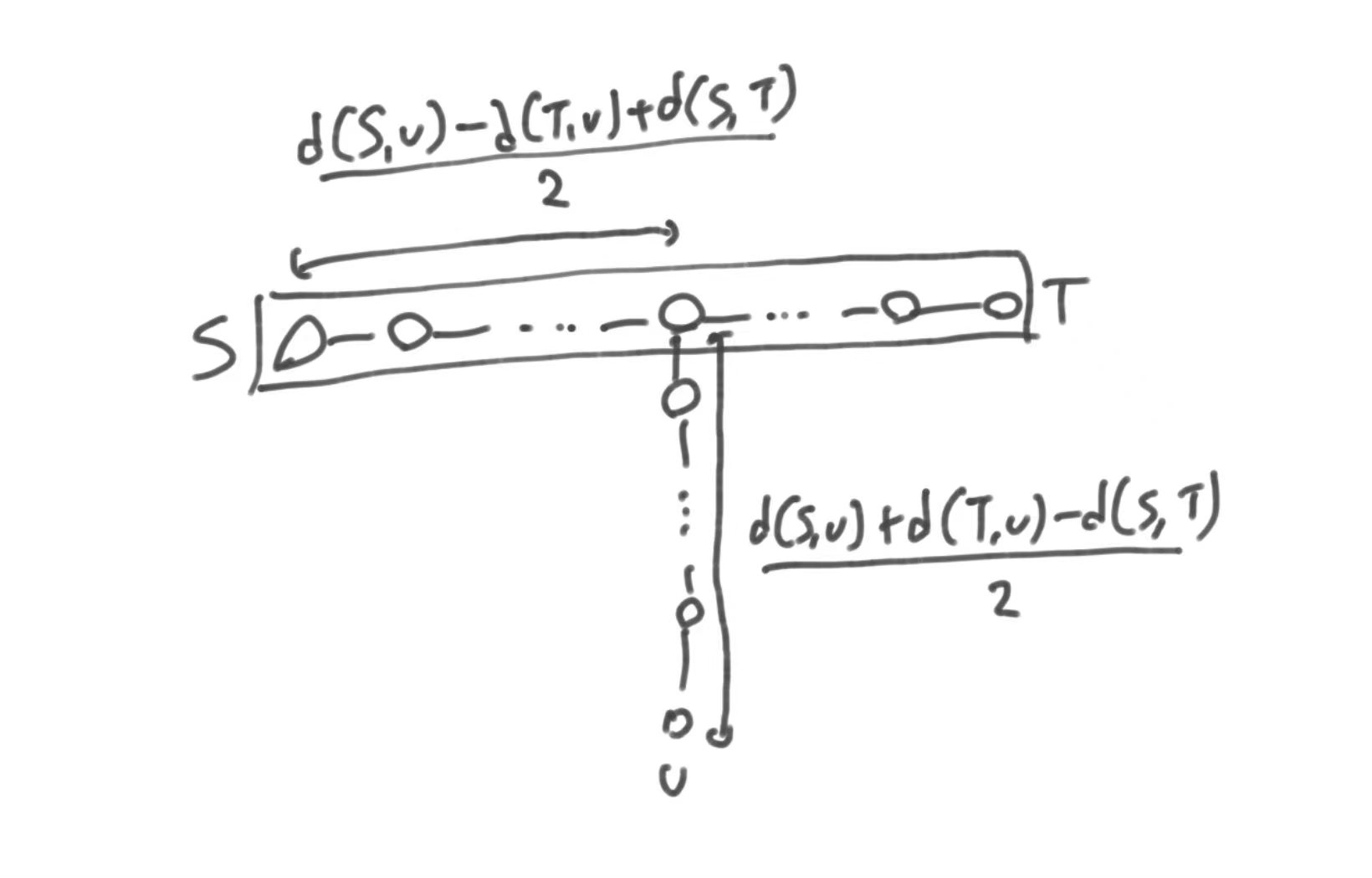
C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;

template<typename T>
struct lca {
    int n, l;
    vector<vector<int>> to;
    vector<vector<T>> co;
    vector<int> dep;
    vector<T> costs;
    vector<vector<int>> par;
    lca(int n): n(n), to(n), co(n), dep(n), costs(n) {
        l = 0;
        while (1<<l <= n) ++l;
        par = vector<vector<int>>(n, vector<int>(l, -1));
    }
    void addEdge(int a, int b, T c=1) {
        to[a].push_back(b); co[a].push_back(c);
        to[b].push_back(a); co[b].push_back(c);
    }
    void dfs(int v, int d=0, T c=0, int p=-1) {
        par[v][0] = p;
        dep[v] = d;
        costs[v] = c;
        rep(i, to[v].size()) {
            int u = to[v][i];
            if (u == p) continue;
            dfs(u, d+1, c+co[v][i], v);
        }
    }
    void init(int root=0) {
        dfs(root);
        rep(i, l-1) {
            rep(v, n) {
                par[v][i+1] = par[v][i]==-1 ? -1 : par[par[v][i]][i];
            }
        }
    }
    // LCA
    int operator()(int a, int b) {
        if (dep[a] > dep[b]) swap(a, b);
        int gap = dep[b]-dep[a];
        for (int i = l-1; i >= 0; --i) {
            int len = 1<<i;
            if (gap >= len) {
                gap -= len;
                b = par[b][i];
            }
        }
        if (a == b) return a;
        for (int i = l-1; i >= 0; --i) {
            int na = par[a][i];
            int nb = par[b][i];
            if (na != nb) a = na, b = nb;
        }
        return par[a][0];
    }
    int length(int a, int b) {
        int c = this->operator()(a, b);
        return dep[a]+dep[b]-dep[c]*2;
    }
    T dist(int a, int b) {
        int c = this->operator()(a, b);
        return costs[a]+costs[b]-costs[c]*2;
    }
};

int main() {
    int n, s, t;
    cin >> n >> s >> t;
    --s; --t;

    lca<int> g(n);
    rep(i, n-1) {
        int a, b;
        cin >> a >> b;
        --a; --b;
        g.addEdge(a, b);
    }
    g.init();

    rep(j, n) {
        int d1 = g.length(s, j);
        int d2 = g.length(t, j);
        int d3 = g.length(s, t);
        int ans = (d1+d2-d3)/2+1;
        cout << ans << '\n';
    }

    return 0;
}

30. 树节点的排序

已知一颗包含 $n$ 个节点的树，求一个 $1$ 到 $n$ 的排列 $p_1, p_2, \cdots, p_n$，使得 $\sum\limits_{i=1}^n \operatorname{dis}(i, p_i)$ 的值最大，其中 dis(i, j) 表示点 $i$ 和点 $j$ 在树上的距离。

限制：

• $2 \leqslant n \leqslant 10^6$
• $0 <$ 边权 $\leqslant 1000$

算法分析

$N \leqslant 5000$：

• 树形dp
• dp[i][j] 表示在以点 $i$ 为根的子树中，选的点深度最大为 $j$ 进行状态转移

$N \leqslant 10^6$：

• 之前那个树形dp可以用长链剖分优化
• 也可以用另一种方法
• 分别考虑每条边对答案的贡献
• 每条边两端连接的连通块大小不妨记为 $x$ 和 $y$
• 那么这条边对答案最多贡献 $2\min(x, y)$ 次
• 即其中一个连通块的 $\min(x, y)$ 个点穿过这条边跑到另一个连通块
• 实际上每条边是可以同时分别取到这个最大值的
• 那么一次 $\operatorname{dfs}$ 过程就能统计出来，只需要额外记录子树大小
• 时间复杂度：$\mathcal{O}(n)$

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;
using ll = long long;
using P = pair<int, int>;

int main() {
    freopen("tree.in", "r", stdin);
    freopen("tree.out", "w", stdout);

    int n;
    cin >> n;

    vector<vector<P>> g(n);
    rep(i, n-1) {
        int a, b, c;
        cin >> a >> b >> c;
        --a; --b;
        g[a].emplace_back(b, c);
        g[b].emplace_back(a, c);
    }

    ll ans = 0;
    vector<int> t(n, 1);
    auto dfs = [&](auto f, int v, int p=-1) -> void {
        for (auto [u, w] : g[v]) {
            if (u == p) continue;
            f(f, u, v);
            t[v] += t[u];
            ans += 2ll*min(t[u], n-t[u])*w;
        }
    };
    dfs(dfs, 0);

    cout << ans << '\n';

    return 0;
}

31. 最远点

现在给你一个 $n$ 个节点的树。你一共要做 $m$ 次操作。每次操作是下列两个操作中的一种：

• 删除树上现存的一条边。
• 查询在节点 $u$ 目前所在的连通块内，离点 $u$ 最远的点的距离。

两点之间的距离定义为两点之间简单路径的边数。

限制：

• $1 \leqslant n, m \leqslant 2 \times 10^5$

算法分析

离线所有操作，把删边换成加边，用并查集维护连通块。

求最远点等效于求直径，一个点到最远点的距离一定在直径的两个端点上。

在维护连通块时，同样可以维护直径，新的直径的两个端点一定在原先的 4 个端点之间。

32. 树的连通子图

给定一棵有 $n$ 个结点的树，$1$ 号点为这棵树的根。请计算，这棵树有多少连通子图，由于答案可能很大，输出答案模 $1,000,000,007$ 的余数即可。

所谓连通子图，是该树的点构成的集合，这些点之间任意两个点的路径上不存在不属于该集合的点。空集不算连通子图。

限制：

• $1 \leqslant n \leqslant 2 \times 10^5$

算法分析

树形dp

记 dp[v] 表示在以点 $v$ 为根的子树中包含点 $v$ 的连通子图个数

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;
using ll = long long;

//const int mod = 998244353;
const int mod = 1000000007;
struct mint {
    ll x;
    mint(ll x=0):x((x%mod+mod)%mod) {}
    mint operator-() const {
        return mint(-x);
    }
    mint& operator+=(const mint a) {
        if ((x += a.x) >= mod) x -= mod;
        return *this;
    }
    mint& operator-=(const mint a) {
        if ((x += mod-a.x) >= mod) x -= mod;
        return *this;
    }
    mint& operator*=(const mint a) {
        (x *= a.x) %= mod;
        return *this;
    }
    mint operator+(const mint a) const {
        return mint(*this) += a;
    }
    mint operator-(const mint a) const {
        return mint(*this) -= a;
    }
    mint operator*(const mint a) const {
        return mint(*this) *= a;
    }
    mint pow(ll t) const {
        if (!t) return 1;
        mint a = pow(t>>1);
        a *= a;
        if (t&1) a *= *this;
        return a;
    }

    // for prime mod
    mint inv() const {
        return pow(mod-2);
    }
    mint& operator/=(const mint a) {
        return *this *= a.inv();
    }
    mint operator/(const mint a) const {
        return mint(*this) /= a;
    }
};
istream& operator>>(istream& is, mint& a) {
    return is >> a.x;
}
ostream& operator<<(ostream& os, const mint& a) {
    return os << a.x;
}

int main() {
    int n;
    cin >> n;

    vector<vector<int>> to(n);
    for (int i = 1; i < n; ++i) {
        int p;
        cin >> p;
        --p;
        to[p].push_back(i);
    }

    mint ans;
    vector<mint> dp(n, 1);
    auto dfs = [&](auto f, int v) -> void {
        for (int u : to[v]) {
            f(f, u);
            dp[v] *= dp[u]+1;
        }
        ans += dp[v];
    };
    dfs(dfs, 0);

    cout << ans << '\n';

    return 0;
}

33. ABC207

给出一棵有 $n$ 个节点的树，每个点可能有一个警卫，每个警卫控制当前节点以及相邻节点。

对每个 $k=0,1,2,\cdots n$，求出恰好有 $k$ 个节点被控制的方案数，并对答案模 $10^9+7$。

限制：

• $1 \leqslant n \leqslant 2000$

算法分析

树上最小支配集的变种题

考虑树形dp

记 dp[v][i][j] 表示在以点 $v$ 为根的子树中满足恰好有 $i$ 个点被控制且点 $v$ 没有被控制/点 $v$ 不在支配集中但被控制/点 $v$ 在支配集中的支配集的个数

C++ 代码

#include <bits/stdc++.h>
#if __has_include(<atcoder/all>)
#include <atcoder/all>
using namespace atcoder;
#endif
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;
using mint = modint1000000007;
using vm = vector<mint>;
using vvm = vector<vm>;

int main() {
    int n;
    cin >> n;

    vector<vector<int>> to(n);
    rep(i, n-1) {
        int a, b;
        cin >> a >> b;
        --a; --b;
        to[a].push_back(b);
        to[b].push_back(a);
    }

    auto dfs = [&](auto& f, int v, int p=-1) -> vvm {
        vvm dp(2, vm(3));
        dp[0][0] = 1;
        dp[1][2] = 1;

        for (int u : to[v]) {
            if (u == p) continue;
            vvm dp_u = f(f, u, v);
            int nv = dp.size(), nu = dp_u.size();
            vvm dp_v(nv+nu-1, vm(3));
            swap(dp, dp_v);
            rep(vi, nv)rep(vj, 3) {
                rep(ui, nu)rep(uj, 3) {
                    mint now = dp_v[vi][vj]*dp_u[ui][uj];
                    if (now.val() == 0) continue;
                    int i = vi+ui, j = -1;
                    if (vj == 0 and uj != 2) {
                        j = 0;
                    }
                    else if (vj == 2) {
                        j = 2;
                    }
                    else {
                        j = 1;
                    }
                    if (vj == 0 and uj == 2) ++i;
                    if (vj == 2 and uj == 0) ++i;
                    dp[i][j] += now;
                }
            } 
        }

        return dp;
    };

    vvm dp = dfs(dfs, 0);
    vm ans(n+1);
    rep(i, n+1)rep(j, 3) ans[i] += dp[i][j];

    rep(i, n+1) cout << ans[i].val() << '\n';

    return 0;
}

34. CF766E

给定一棵 $n$ 个点的树，点 $i$ 的点权为 $a_i$。定义 $f(u, v)$ 为从树链 $u, v$ 上所有点的点权的异或和。

求 $\sum\limits_{u=1}^n\sum\limits_{v=u}^n f(u, v)$

限制：

• $1 \leqslant n \leqslant 10^5$
• $0 \leqslant a_i \leqslant 10^6$

算法分析

本题实际上是 异或和之和 的树上版本

考虑树形dp
记 dp[v][b][x] 表示在以点 $v$ 为根的子树中从点 $v$ 出发且二进制下第 $b$ 位的异或和为 $x$ 的树链个数

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;
using ll = long long;

int main() {
    cin.tie(nullptr) -> sync_with_stdio(false);

    int n;
    cin >> n;

    vector<int> a(n);
    rep(i, n) cin >> a[i];

    vector<vector<int>> to(n);
    rep(i, n-1) {
        int a, b;
        cin >> a >> b;
        --a; --b;
        to[a].push_back(b);
        to[b].push_back(a);
    }

    ll ans = 0;
    vector dp(n, vector<ll>(2));
    auto dfs = [&](auto& f, int v, int p, int b) -> void {
        int x = a[v]>>b&1;
        dp[v][0] = dp[v][1] = 0;
        dp[v][x] = 1;

        ans += dp[v][1]*(1<<b);
        for (int u : to[v]) {
            if (u == p) continue;
            f(f, u, v, b);

            ll now = 0;
            now += dp[v][0]*dp[u][1];
            now += dp[v][1]*dp[u][0];
            ans += now*(1<<b);

            dp[v][0] += dp[u][x];
            dp[v][1] += dp[u][!x];
        }
    };

    rep(i, 20) dfs(dfs, 0, -1, i);

    cout << ans << '\n';

    return 0;
}

35. ABC337G

给定一颗 $N$ 个点的树 $T$，第 $i$ 条边连接点 $u_i$ 和点 $v_i$ 。

对于 $T$ 上的点 $u$，按如下方式定义 $f(u)$：

• $f(u):=$ $T$ 上满足以下两个条件的点 $v$ 和点 $w$ 的二元组的个数
  • 点 $w$ 出现在树链 $(u, v)$ 上
  • $v < w$

其中，点 $w$ 也可以和树链 $(u, v)$ 两端点中任意一点重合。

请求出 $f(1), f(2), \cdots, f(N)$ 的值。

限制：

• $2 \leqslant N \leqslant 2 \times 10^5$

算法分析

先求出 $f(1)$，再通过换根求出其他点的 $f(u)$
如何快速求 $f(1)$？
方法之一是求出以点 $u$ 为根的子树中包含的点 $v(v < u)$ 的个数
- 这个可以通过树状数组维护 $dfs$ 序获得

当点 $A$ 是点 $B$ 的父节点时，可以通过 $f(A)$ 快速推出 $f(B)$ 吗？

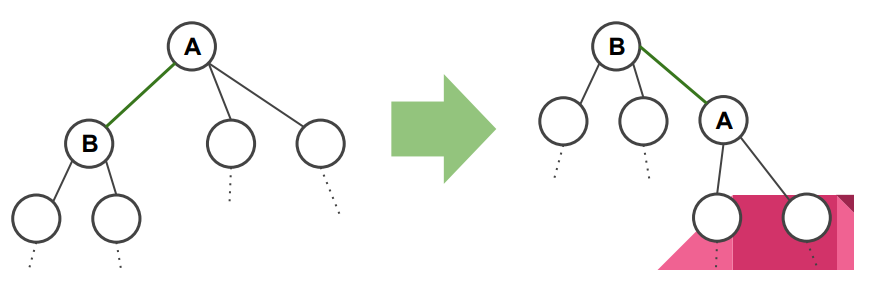
• 减去的部分
• 蓝框中小于 $A$ 的点

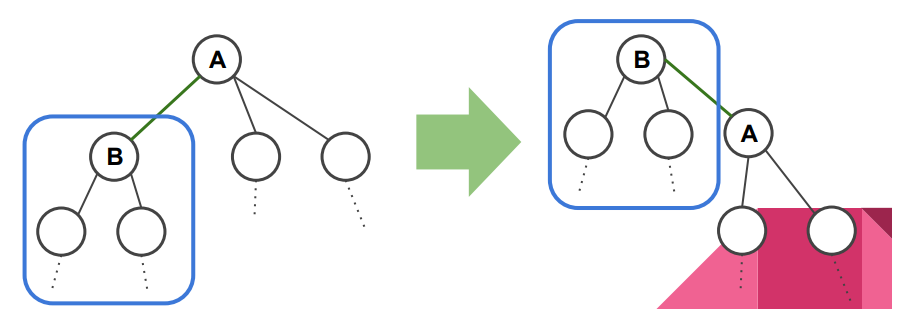
• 增加的部分
• 红框中小于 $B$ 的点

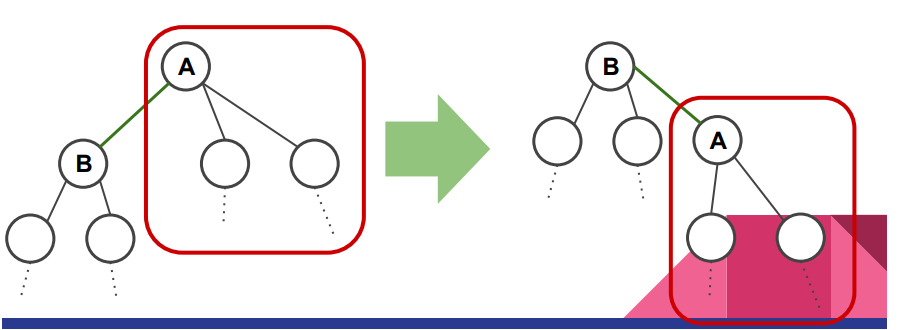
C++ 代码

#include <bits/stdc++.h>
#if __has_include(<atcoder/all>)
#include <atcoder/all>
using namespace atcoder;
#endif
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;
using ll = long long;

int main() {
    int n;
    cin >> n;

    vector<vector<int>> to(n);
    rep(i, n-1) {
        int a, b;
        cin >> a >> b;
        --a; --b;
        to[a].push_back(b);
        to[b].push_back(a);
    }

    fenwick_tree<int> t(n);
    vector<ll> ans(n);
    vector<int> d(n);
    vector<vector<int>> dc(n);
    auto dfs = [&](auto& f, int v, int p=-1) -> void {
        t.add(v, 1);
        d[v] -= t.sum(0, v);
        for (int u : to[v]) {
            dc[v].push_back(0);
            if (u == p) continue;
            dc[v].back() -= t.sum(0, v);
            f(f, u, v);
            dc[v].back() += t.sum(0, v);
        }
        d[v] += t.sum(0, v);
    };
    dfs(dfs, 0);

    ll base = 0;
    rep(v, n) base += d[v];

    auto dfs2 = [&](auto& f, int v, ll x, int p=-1) -> void {
        ans[v] = x;
        rep(i, to[v].size()) {
            int u = to[v][i];
            if (u == p) continue;
            ll nx = x;
            nx -= dc[v][i];
            nx += u-d[u];
            f(f, u, nx, v);
        }
    };
    dfs2(dfs2, 0, base);

    rep(i, n) cout << ans[i] << ' ';

    return 0;
}

36. ABC248G

给定一颗树有 $n$ 个结点，每个结点上有一个权值 $a_i$,对于每条至少包含两个点的简单路径，它的贡献为路径上点的数量(包括端点) $\times$ 路径上所有点的 $a_i$ 的最大公约数。
求所有简单路径的贡献之和，对 $998244353$ 取模。

限制：

• $2 \leqslant n \leqslant 10^5$
• $1 \leqslant a_i \leqslant 10^5$

算法分析

记 $f(x)$ 表示点权都是 $x$ 的倍数构成的树链的长度总和
记 $g(x)$ 表示点权的 $\gcd$ 等于 $x$ 的树链的长度总和
那么 $g(x) = f(x) - f(2x) - f(3x) - \cdots - f(px) - \cdots$，其中 $p$ 是指小于 $1e5$ 的素数

枚举 $x = 1, 2, \cdots, 10^5$，分别对树上点权为 $x$ 的倍数的点进行染色，我们只需求出每个连通块中的所有树链的总和即可
具体地，注意到，树链的长度可拆解为树链两端点的距离+$1$，而对于某个连通块的 $\sum$ 树链两端点的距离其实就是上面的 $19$ 题，而 $\sum 1$ 等价于在连通块中任取 $2$ 个点的方案数

C++ 代码

#include <bits/stdc++.h>
#if __has_include(<atcoder/all>)
#include <atcoder/all>
using namespace atcoder;
#endif
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;
using ll = long long;
using mint = modint998244353;

const int M = 100002;

struct Sieve {
    int n;
    vector<int> f, primes;
    Sieve(int n=1): n(n), f(n+1) {
        f[0] = f[1] = -1;
        for (ll i = 2; i <= n; ++i) {
            if (f[i]) continue;
            primes.push_back(i);
            f[i] = i;
            for (ll j = i*i; j <= n; j += i) {
                if (!f[j]) f[j] = i;
            }
        }
    }
};

int main() {
    cin.tie(nullptr) -> sync_with_stdio(false);

    vector<int> ps;
    {
        Sieve s(M);
        ps = s.primes;
    }

    int n;
    cin >> n;

    vector<int> a(n);
    rep(i, n) cin >> a[i];

    vector<vector<int>> is(M);
    rep(i, n) is[a[i]].push_back(i);
    for (int p : ps) {
        for (int i = M/p; i >= 1; --i) {
            is[i].insert(is[i].end(), is[i*p].begin(), is[i*p].end());
        }
    }

    vector<vector<int>> to(n);
    rep(i, n-1) {
        int a, b;
        cin >> a >> b;
        --a; --b;
        to[a].push_back(b);
        to[b].push_back(a);
    }

    vector<mint> f(M);
    vector<bool> live(n);
    vector<bool> used(n);
    for (int x = 1; x < M; ++x) {
        vector<int>& vs = is[x];
        for (int v : vs) live[v] = true;
        mint t1, t2;
        auto dfs = [&](auto& f, int v) -> int {
            int res = 1;
            used[v] = true;
            for (int u : to[v]) {
                if (!live[u] or used[u]) continue;
                int r = f(f, u);
                t1 += r; t2 += (ll)r*r;
                res += r;
            }
            return res;
        };
        for (int v : vs) if (!used[v]) {
            t1 = t2 = 0;
            int s = dfs(dfs, v);
            f[x] += t1*s - t2 + ll(s-1)*s/2;
        }

        for (int v : vs) live[v] = false;
        for (int v : vs) used[v] = false;
    }

    for (int p : ps) {
        for (int i = 1; i*p < M; ++i) {
            f[i] -= f[i*p];
        }
    }

    mint ans;
    for (int x = 1; x < M; ++x) ans += f[x]*x;

    cout << ans.val() << '\n';

    return 0;
}

37. 彩色树（二）

给定一棵 $n$ 个点的树，$1$ 号点为根。每个点有一个颜色，点 $i$ 的颜色为 $c_i$、父结点为 $p_i$。

除 $1$ 号点外，请你求出，对于每个点，有多少条起点和终点颜色相同路径经过了该点到他父亲的边。（只考虑路径起点和终点即可，对路径上经过的其他点的颜色不做要求）

限制：

• $2 \leqslant n \leqslant 10^5$
• $1 \leqslant c_i \leqslant n$

算法分析

问题可以看成对于每个点 $u$ 统计有多少个点对 $(x, y)$，满足 $c_x=c_y$ 且 $x$ 在 $u$ 子树内，$y$ 在 $u$ 子树外。考虑颜色 $t$ 在 $u$ 子树内出现了 $\operatorname{cnt}_t$ 次，该颜色在整棵树中出现了 $\operatorname{tot}_t$ 次，那么该颜色对点 $u$ 的贡献即为 $\operatorname{cnt}_t \times (\operatorname{tot}_t-\operatorname{cnt}_t)$，dsu on tree 的时候维护子树内每种颜色的出现次数，更新的时候更新贡献就好了。

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;
using ll = long long;

int main() {
    cin.tie(nullptr) -> sync_with_stdio(false);

    int n;
    cin >> n;

    vector<int> c(n);
    rep(i, n) cin >> c[i];
    rep(i, n) c[i]--;
    vector<int> tot(n);
    rep(i, n) tot[c[i]]++;

    vector<vector<int>> to(n);
    for (int i = 1; i < n; ++i) {
        int p;
        cin >> p;
        to[p-1].push_back(i);
    }

    vector<ll> ans(n);
    vector<map<int, int>> dc(n);
    auto dfs = [&](auto& f, int v) -> void {
        ans[v] = tot[c[v]]-1;
        dc[v][c[v]] = 1;
        for (int u : to[v]) {
            f(f, u);

            if (dc[v].size() < dc[u].size()) {
                ans[v] = ans[u];
                swap(dc[v], dc[u]);
            }
            for (auto [x, y] : dc[u]) {
                ans[v] -= dc[v][x] * (tot[x]-dc[v][x]);
                dc[v][x] += y;
                ans[v] += dc[v][x] * (tot[x]-dc[v][x]);
            }

            dc[u].clear();
        }
    };
    dfs(dfs, 0);

    for (int i = 1; i < n; ++i) cout << ans[i] << ' ';

    return 0;
}

38. Preserve Connectivity

给定 $N$ 个点的树，顶点的编号分别为 $1, 2, \cdots, N$。第 $i$ 条边连接点 $A_i$ 和点 $B_i$。
按 $j = 1, 2, \cdots, Q$ 的顺序回答以下形式的询问：

• 从 $N-1$ 条边中选几条边留下
• 当我们将没有选到的边删除时，应保证点 $V_{j,1}, V_{j,2}, \cdots, V_{j,K_j}$ 连通
• 最少要选几条边？

限制：

• $2 \leqslant N \leqslant 10^5$
• $1 \leqslant A_i < B_i \leqslant N$
• $2 \leqslant K_j \leqslant N$
• $1 \leqslant V_{j,1} < V_{j,2} < \cdots, < V_{j,K_j} \leqslant N$
• $K_1 + K_2 + \cdots + K_Q \leqslant 2 \times 10^5$

算法分析

虚树dp的板题

答案就是包含这 $K$ 个点的最小连通子图的边权总和

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;
using P = pair<int, int>;

// Lowest Common Ancestor by binary lifting
template<typename T=int> // T: type of cost
struct lca {
  int n, root, l;
  vector<vector<int>> to;
  vector<vector<T>> co;
  vector<int> dep;
  vector<T> costs;
  vector<vector<int>> par;
  lca(int n):n(n),to(n),co(n),dep(n),costs(n) {
    l = 0;
    while ((1<<l) < n) ++l;
    par = vector<vector<int>>(n+1,vector<int>(l,n));
  }
  void addEdge(int a, int b, T c=0) {
    to[a].push_back(b); co[a].push_back(c);
    to[b].push_back(a); co[b].push_back(c);
  }
  void dfs(int v, int d=0, T c=0, int p=-1) {
    if (p != -1) par[v][0] = p;
    dep[v] = d;
    costs[v] = c;
    for (int i = 0; i < to[v].size(); ++i) {
      int u = to[v][i];
      if (u == p) continue;
      dfs(u, d+1, c+co[v][i], v);
    }
  }

  void init(int _root=0) {
    root = _root;
    dfs(root);
    for (int i = 0; i < l-1; ++i) {
      for (int v = 0; v < n; ++v) {
        par[v][i+1] = par[par[v][i]][i];
      }
    }
  }
  // LCA
  int up(int v, int k) {
    for (int i = l-1; i >= 0; --i) {
      int len = 1<<i;
      if (k >= len) k -= len, v = par[v][i];
    }
    return v;
  }
  int operator()(int a, int b) {
    if (dep[a] > dep[b]) swap(a,b);
    b = up(b, dep[b]-dep[a]);
    if (a == b) return a;
    for (int i = l-1; i >= 0; --i) {
      int na = par[a][i], nb = par[b][i];
      if (na != nb) a = na, b = nb;
    }
    return par[a][0];
  }
  int length(int a, int b) {
    int c = (*this)(a,b);
    return dep[a]+dep[b]-dep[c]*2;
  }
  T dist(int a, int b) {
    int c = (*this)(a,b);
    return costs[a]+costs[b]-costs[c]*2;
  }
  int getp(int v) { return par[v][0]; }
};

int main() {
    int n;
    cin >> n;

    vector<vector<int>> to(n);
    lca g(n);
    rep(i, n-1) {
        int a, b;
        cin >> a >> b;
        --a; --b;
        g.addEdge(a, b);
        to[a].push_back(b);
        to[b].push_back(a);
    }
    g.init();

    vector<int> in(n), out(n);
    {
        int k = 0;
        auto dfs = [&](auto& f, int v, int p=-1) -> void {
            in[v] = k++;
            for (int u : to[v]) {
                if (u == p) continue;
                f(f, u, v);
            }
            out[v] = k;
        };
        dfs(dfs, 0);
    }

    int q;
    cin >> q;
    rep(qi, q) {
        int k;
        cin >> k;
        vector<int> vs;
        rep(i, k) {
            int v;
            cin >> v;
            --v;
            vs.push_back(v);
        }
        sort(vs.begin(), vs.end(), [&](int a, int b) { return in[a] < in[b]; });
        vs.push_back(vs[0]);
        int ans = 0;
        rep(i, k) {
            int a = vs[i], b = vs[i+1];
            ans += g.length(a, b);
        }
        ans /= 2;
        cout << ans << '\n';
    }

    return 0;
}

39. CF1923E

给定一颗 $n$ 个点的树，点的编号分别为 $1 \sim n$。每个点都被染上某种颜色，用 $1 \sim n$ 之间的某个整数表示。

将树上的一条简单路径称为美丽的当且仅当满足以下条件：

• 至少包含两个点
• 路径上首尾两端点的颜色相同
• 路径上没有其他点和首位两端的颜色相同

统计树上美丽的简单路径的个数。

限制：

• $2 \leqslant n \leqslant 2 \times 10^5$
• $1 \leqslant c_i \leqslant n$

算法分析

记 cnt[c] 表示假设当前点的颜色为 $c$，当不穿过颜色 $c$ 的顶点时，可以到达当前点的颜色 $c$ 的顶点个数
然后跑一遍 $\operatorname{dfs}$ 即可

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;
using ll = long long;

void solve() {
    int n;
    cin >> n;

    vector<int> c(n);
    rep(i, n) cin >> c[i];
    rep(i, n) c[i]--;

    vector<vector<int>> to(n);
    rep(i, n-1) {
        int a, b;
        cin >> a >> b;
        --a; --b;
        to[a].push_back(b);
        to[b].push_back(a);
    }

    ll ans = 0;
    vector<int> cnt(n);
    auto dfs = [&](auto& f, int v, int p=-1) -> void {
        int pre = cnt[c[v]];
        ans += pre;
        for (int u : to[v]) {
            if (u == p) continue;
            cnt[c[v]] = 1;
            f(f, u, v);
        }
        cnt[c[v]] = pre+1;
    }; 
    dfs(dfs, 0);

    cout << ans << '\n';
}

int main() {
    cin.tie(nullptr) -> sync_with_stdio(false);

    int t;
    cin >> t;

    while (t--) solve();

    return 0;
}

40. ABC259F

给定一棵 $n$ 个节点的树，每条边有一个权值 $w_i$。

现要求选择一些边，使得每个节点 $i$ 相邻的边中被选中的不超过 $d_i$ 条，请求出最大边权和。

限制：

• $2 \times n \leqslant 3 \times 10^5$
• $|w_i| \leqslant 10^9$
• $d_i$ 是不超过点 $i$ 的度数的非负整数

算法分析

首先考虑能否贪心，也就是每次尽可能选边权最大的边

反例：

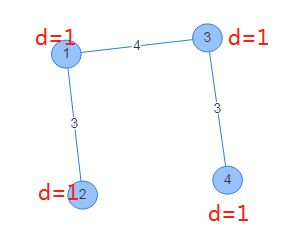
按贪心做法，我们只能取到 $4$，但更优的选法是选 $2$ 个 $3$

下面来考虑树形 $\rm{dp}$

记 dp[v][0/1] 表示在点 $v$ 的子树中不选择或选择点 $v$ 的父边时所能达到的最大价值

然后考虑贪心地转移:

先把每个 dp[v][0/1] 都初始化成不选其父边

若不选点 $v$ 的父边，则至多可以选择 $d[v]$ 条点 $v$ 的儿子边
若选点 $v$ 的父边，则至多可以选择 $d[v]-1$ 条点 $v$ 的儿子边
为了价值最大化，应该尽可能选择那些使得 dp[v][1] - dp[v][0] 比较大的点 $v$ 的儿子边

特别地，当 $d[v] = 0$ 时，需要令 $dp[v][1] = -\infty$

弱化版：保安站岗

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;
using ll = long long;

struct Edge {
    int to, cost;
    Edge() {}
    Edge(int to, int cost): to(to), cost(cost) {}
};

int main() {
    int n;
    cin >> n;

    vector<int> d(n);
    rep(i, n) cin >> d[i];

    vector<vector<Edge>> g(n); 
    rep(i, n-1) {
        int a, b, c;
        cin >> a >> b >> c;
        --a; --b;
        g[a].emplace_back(b, c);
        g[b].emplace_back(a, c);
    }

    const ll INF = 1e18;
    auto dfs = [&](auto& f, int v, int p=-1) -> vector<ll> {
        vector<ll> e(1, 0); 
        ll base = 0;
        for (auto [u, c] : g[v]) {
            if (u == p) continue;
            auto r = f(f, u, v);
            r[1] += max(0, c);
            e.push_back(max(0ll, r[1]-r[0]));
            base += r[0];
        }
        vector<ll> res(2, base);
        sort(e.rbegin(), e.rend());
        rep(i, d[v]) res[0] += e[i];
        rep(i, d[v]-1) res[1] += e[i];
        if (d[v] == 0) res[1] = -INF;
        return res;
    };

    auto dp = dfs(dfs, 0);
    cout << dp[0] << '\n';

    return 0;
}

41. 树的支配集（二）

给定一棵拥有 $n$ 个结点的树，$1$ 号点为这棵树的根，请找出这棵树的 超级支配集。

所谓超级支配集，是一个由树上结点构成的子集，树上不属于这个子集的结点，都能找到有且仅有一个邻居属于这个子集，且该支配集是所有满足条件中，包含点数最少的。

限制：

• $1 \leqslant n \leqslant 10^5$

算法分析

考虑树形dp
状态表示：

• dp[v][0]：v 在支配集中
• dp[v][1]：v 不在支配集中，但父节点在支配集中
• dp[v][2]：v 不在支配集中且父节点也不在支配集中，但有且仅有一个儿子节点在支配集中

代码实现

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;

int main() {
    int n;
    cin >> n;

    vector<vector<int>> to(n);
    for (int i = 1; i < n; ++i) {
        int p;
        cin >> p;
        --p; 
        to[p].push_back(i);
        to[i].push_back(p);
    }

    vector dp(n, vector<int>(3));
    auto dfs = [&](auto& f, int v, int p=-1) -> void {
        dp[v][0] = 1; 
        dp[v][1] = 0; 
        dp[v][2] = n; 
        for (int u : to[v]) {
            if (u == p) continue;
            f(f, u, v);
            dp[v][0] += min(dp[u][0], dp[u][1]);
            dp[v][1] += dp[u][2];
        }
        for (int u : to[v]) {
            if (u == p) continue;
            dp[v][2] = min(dp[v][2], dp[v][1]+dp[u][0]-dp[u][2]);
        }
    };
    dfs(dfs, 0);

    int ans = min(dp[0][0], dp[0][2]);
    cout << ans << '\n';

    return 0;
}

42. LCA求和

给定一颗 $n$ 个点的树，点的编号为 $1 \sim n$，其中 $1$ 号点为根
求 $\sum_{i=1}^n\sum_{j=1}^n \operatorname{lca}(i, j)$ .
其中 $\operatorname{lca}(i, j)$ 指点 $u$ 和点 $v$ 的最近公共祖先的编号.

限制：

• $1 \leqslant n \leqslant 2 \times 10^5$

算法分析

注意到如果点 $i$ 和点 $j$ 有一个点出现在点 $u$ 上，而另一个点出现在它的子孙节点上的话，那么此时 $\operatorname{lca}(i, j)$ 显然是 $u$
另外，如果点 $i$ 和点 $j$ 分别出现在点 $v$ 的不同子树上的话，此时它们的 $\operatorname{lca}$ 也是 $v$
假设以点 $v$ 为根的子树大小为 $t[v]$
那么，最后的答案就是 $\sum\limits_{v} \left(v + v \times t[u] \times (t[v] - t[u] + 1)\right)$，其中点 $u$ 是点 $v$ 的子节点。

代码实现

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;
using ll = long long;

int main() {
    int n;
    cin >> n;

    vector<vector<int>> to(n);
    rep(i, n-1) {
        int a, b;
        cin >> a >> b;
        --a; --b;
        to[a].push_back(b);
        to[b].push_back(a);
    }

    ll ans = 0;
    vector<ll> t(n, 1);
    auto dfs = [&](auto& f, int v, int p=-1) -> void {
        ans += v+1;
        for (int u : to[v]) {
            if (u == p) continue;
            f(f, u, v);
            t[v] += t[u];
        }
        for (int u : to[v]) {
            if (u == p) continue;
            ans += ll(v+1)*t[u]*(t[v]-t[u]+1);
        }
    };
    dfs(dfs, 0);

    cout << ans << '\n';

    return 0;
}

43. We Need Both a and b

给定一颗 $n$ 个点的树，点的编号为 $1 \sim n$，第 $i$ 条边连接点 $a_i$ 和点 $b_i$ 。
每个点上写有字符 a 或 b，在点 $i$ 上写的字符是 $c_i$ 。
删除至少 $0$ 条边的方案数为 $2^{n-1}$，问有多少种删边方案使得删边后的每个连通块中都包含 a 和 b 两种字符。并对答案模 $10^9 + 7$ 。

限制：

• $2 \leqslant n \leqslant 10^5$

算法分析

记 dp[v][i] 表示在以点 $v$ 为根的子树中，包含点 $v$ 的连通块中仅含有字符 a(i = 0)/仅含有字符 b(i = 1)/同时含有字符 a 和 b(i = 2) 时的合法删边方案数

代码实现

#include <bits/stdc++.h>
#if __has_include(<atcoder/all>)
#include <atcoder/all>
using namespace atcoder;
#endif
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;
using mint = modint1000000007;

int main() {
    int n;
    cin >> n;

    vector<char> c(n);
    rep(i, n) cin >> c[i];

    vector<vector<int>> to(n);
    rep(i, n-1) {
        int a, b;
        cin >> a >> b;
        --a; --b;
        to[a].push_back(b);
        to[b].push_back(a);
    }

    vector dp(n, vector<mint>(3));
    auto dfs = [&](auto& f, int v, int p=-1) -> void {
        mint val1 = 1, val2 = 1;
        for (int u : to[v]) {
            if (u == p) continue;
            f(f, u, v);
            if (c[v] == 'a') {
                val1 *= dp[u][0] + dp[u][2];
                val2 *= dp[u][0] + dp[u][1] + 2*dp[u][2];
            }  
            if (c[v] == 'b') {
                val1 *= dp[u][1] + dp[u][2];
                val2 *= dp[u][0] + dp[u][1] + 2*dp[u][2];
            }
        }

        if (c[v] == 'a') {
            dp[v][0] = val1;
            dp[v][2] = val2-val1;
        }
        if (c[v] == 'b') {
            dp[v][1] = val1;
            dp[v][2] = val2-val1;
        }
    };
    dfs(dfs, 0);

    mint ans = dp[0][2];
    cout << ans.val() << '\n';

    return 0;
}

44. 树链

现给定一棵以 $1$ 号点为根的树，第 $i$ 个点的点权为 $x_i$，父节点为 $p_i$（$1$ 号点没有父节点）。请你在树上找到两条没有交集链（一个点也可以是一条链），使得所选中的两条链上的点权之和最大，求满足条件的最大点权和。

限制：

• $2 \leqslant n \leqslant 10^5$
• $1 \leqslant x_i \leqslant 10^9$

算法分析

树形dp好题
状态定义：

• dp[v][0]：在以点 $v$ 为根的子树中选出两条不相交的链的最大值
• dp[v][1]：在以点 $v$ 为根的子树中选出一条链的最大值
• dp[v][2]：在以点 $v$ 为根的子树中从点 $v$ 到叶子节点加上一条与之不相交的链的最大值
• dp[v][3]：$\max\{dp[u][1]\}$
• dp[v][4]：在以点 $v$ 为根的子树中从点 $v$ 到叶子节点的最大值

代码实现

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;
using ll = long long;

inline void chmax(ll& x, ll y) { if (x < y) x = y; }

int main() {
    int n;
    cin >> n;

    vector<vector<int>> to(n);
    for (int i = 1; i < n; ++i) {
        int p; cin >> p;
        to[p-1].push_back(i);
    }

    vector<int> x(n);
    rep(i, n) cin >> x[i];

    vector dp(n, vector<ll>(5));
    auto dfs = [&](auto& f, int v) -> void {
        dp[v][0] = dp[v][1] = dp[v][2] = dp[v][4] = x[v];
        for (int u : to[v]) {
            f(f, u);

            chmax(dp[v][0], dp[u][0]);
            chmax(dp[v][0], dp[v][1]+dp[u][1]);
            chmax(dp[v][0], dp[v][4]+dp[u][2]);
            chmax(dp[v][0], dp[u][4]+dp[v][2]);

            chmax(dp[v][1], dp[u][1]);
            chmax(dp[v][1], dp[v][4]+dp[u][4]);

            chmax(dp[v][2], dp[u][2]+x[v]);
            chmax(dp[v][2], dp[v][4]+dp[u][1]);
            chmax(dp[v][2], dp[u][4]+dp[v][3]+x[v]);

            chmax(dp[v][3], dp[u][1]);

            chmax(dp[v][4], dp[u][4]+x[v]);
        }
    };
    dfs(dfs, 0);

    cout << dp[0][0] << '\n';

    return 0;
}

45. 树的计数

小爱想要画一棵 $n$ 个节点的有根树，节点编号分别为 $1, \cdots, n$，他告诉了你他希望每个节点在这棵树上的深度 $d_i$，其中根节点深度为 $1$。

请你根据给定信息，帮忙计算出有多少棵树满足小爱的要求？由于答案可能很大，请你输出对 $10^9+7$ 取模后的结果。

限制：

• $1 \leqslant n \leqslant 10^5$

算法分析

注意到，深度为 $2$ 的点一定是深度为 $1$ 的点的儿子节点，深度为 $3$ 的点一定是深度为 $2$ 的点的儿子节点.....那么深度为 $i$ 的点可以是深度为 $i - 1$ 的儿子节点，对于此题是一个经典的分步乘法计数原理，把深度为 $2$ 的儿子节点确定下来是第一步，深度为 $3$ 的儿子节点确定下来是第二步......

原题：Counting of Trees

代码实现

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;
using ll = long long;

//const int mod = 998244353;
const int mod = 1000000007;
struct mint {
    ll x;
    mint(ll x=0):x((x%mod+mod)%mod) {}
    mint operator-() const {
        return mint(-x);
    }
    mint& operator+=(const mint a) {
        if ((x += a.x) >= mod) x -= mod;
        return *this;
    }
    mint& operator-=(const mint a) {
        if ((x += mod-a.x) >= mod) x -= mod;
        return *this;
    }
    mint& operator*=(const mint a) {
        (x *= a.x) %= mod;
        return *this;
    }
    mint operator+(const mint a) const {
        return mint(*this) += a;
    }
    mint operator-(const mint a) const {
        return mint(*this) -= a;
    }
    mint operator*(const mint a) const {
        return mint(*this) *= a;
    }
    mint pow(ll t) const {
        if (!t) return 1;
        mint a = pow(t>>1);
        a *= a;
        if (t&1) a *= *this;
        return a;
    }

    // for prime mod
    mint inv() const {
        return pow(mod-2);
    }
    mint& operator/=(const mint a) {
        return *this *= a.inv();
    }
    mint operator/(const mint a) const {
        return mint(*this) /= a;
    }
};
istream& operator>>(istream& is, mint& a) {
    return is >> a.x;
}
ostream& operator<<(ostream& os, const mint& a) {
    return os << a.x;
}

int main() {
    int n;
    cin >> n;

    vector<int> c(n);
    rep(i, n) {
        int a;
        cin >> a;
        c[a]++;
    }

    if (c[1] != 1) {
        puts("0");
        return 0;
    }

    mint ans = 1, pre = 1;
    for (int i = 1; i <= n-1; ++i) {
        rep(j, c[i]) ans *= pre;
        pre = c[i];
    }

    cout << ans << '\n';

    return 0;
}

46. Product on Tree

给定一个长度为 $N$ 的非负整数序列以及一颗包含 $N$ 个点的树。点的编号分别为 $1, 2, \cdots, N$，第 $i$ 条边连接点 $U_i$ 和点 $V_i$ 。
对于树上不同的两个点 $i, j$ 的费用 $f(i, j)$ 定义如下：

• 点 $i$ 到点 $j$ 的最短路径上的点分别为 $p_1(=i), p_2, \cdots, p_k(=j)$，此时，$f(i, j) = A_{p_1} \times A_{p_2} \times \cdots \times A_{p_k}$ .

求 $\displaystyle \sum_{i=1}^{N-1}\sum_{j=i+1}^N f(i, j) \bmod 998244353$ .

限制：

• $2 \leqslant N \leqslant 2 \times 10^5$
• $0 \leqslant A_i < 998244353$

算法分析

记 dp[v] 表示在以点 $v$ 根的子树中，从点 $v$ 到子树中所有点构成的树链费用总和

转移方程：

$$ dp[v] = \sum dp[u] \times A_v \, , ~ \text{其中点} ~ u ~ \text{是点} ~ v ~ \text{的子节点} $$

贡献分成两部分：

• 子树根节点到子树中的每个点构成的树链
• 当前子树中的点和其他子树中的点构成的树链

代码实现

#include <bits/stdc++.h>
#if __has_include(<atcoder/all>)
#include <atcoder/all>
using namespace atcoder;
#endif
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;
using mint = modint998244353;

int main() {
    cin.tie(nullptr) -> sync_with_stdio(false);

    int n;
    cin >> n;

    vector<int> a(n);
    rep(i, n) cin >> a[i];

    vector<vector<int>> to(n);
    rep(i, n-1) {
        int u, v;
        cin >> u >> v;
        --u; --v;
        to[u].push_back(v);
        to[v].push_back(u);
    }

    mint ans;
    vector<mint> dp(n);
    auto dfs = [&](auto& f, int v, int p=-1) -> void {
        dp[v] = a[v];
        for (int u : to[v]) {
            if (u == p) continue;
            f(f, u, v);
            ans += dp[v]*dp[u];
            dp[v] += dp[u]*a[v];
        }
    };
    dfs(dfs, 0);

    cout << ans.val() << '\n';

    return 0;
}

47. Add One Edge 2

统计有多少种方法给树加一条边使得环上每个点的度数都是 $3$

限制：

• $3 \leqslant N \leqslant 2 \times 10^5$

算法分析

本质上是统计有多少个点对满足除了这两个点的度数以外位于这两个点的路径上的其他点的度数都是 $3$

记 dp[v] 表示在点 $v$ 为根的子树中从点 $v$ 开始的类似 33...32 的路径数
答案有两种情况：
一种是当点 $v$ 的度数是 $2$ 时，对答案的贡献就是 $\sum dp[u]$，其中点 $u$ 是点 $v$ 的儿子节点
另一种是当点 $v$ 的度数是 $3$ 时，对答案的贡献就是以点 $v$ 为 $lca$ 的两边都是 33...2 形式的路径数
注意第一种会将 22 统计进去，所以最后要减去这一部分的贡献才是正确答案

代码实现

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;
using ll = long long;

int main() {
    int n;
    cin >> n;

    vector<vector<int>> to(n);
    rep(i, n-1) {
        int a, b;
        cin >> a >> b;
        --a; --b;
        to[a].push_back(b);
        to[b].push_back(a);
    }

    vector<int> deg(n);
    rep(i, n) deg[i] = to[i].size();

    ll ans = 0;
    vector<ll> dp(n);
    auto dfs = [&](auto& f, int v, int p=-1) -> void {
        for (int u : to[v]) {
            if (u == p) continue;
            f(f, u, v);
            if (deg[v] == 3) {
                ans += dp[v]*dp[u];
            }
            if (deg[v] == 3) dp[v] += dp[u];
            if (deg[v] == 2) {
                ans += dp[u];
                if (deg[u] == 2) ans--;
            }
        }
        if (deg[v] == 2) dp[v]++;
    };
    dfs(dfs, 0);

    cout << ans << '\n';

    return 0;
}

48. 直径之和

图 $G$ 上有 $n$ 个点，依次从 $1$ 到 $n$ 编号，初始图上没有边，将有 $n−1$ 次操作来添加长度均为 $1$ 的边，保证图时刻是一个森林（每个连通块都分别构成树），每次加边后你需要计算森林中每棵树的直径长度之和。

直径长度定义为树中最远的两个点之间的距离，距离定义为最短路径上的边权和。一个点的树的直径长度是 $0$。

为了保证你真的在即时处理询问，而不是把它们存下来之后慢慢处理，你需要维护一个初值为 $0$ 的变量 $var$，每次加边给定 $a,b$，你需要计算 $u=a \oplus var$，$v=b \oplus var$，并在
$u,v$ 之间加边，保证 $1 \leqslant u,v \leqslant n$，加边之后记当前每棵树的直径长度之和为 $d$，令
$var=d \oplus var$。

限制：

• $1 \leqslant n \leqslant 10^5$
• $0 \leqslant a, b \leqslant 2n$
• $1 \leqslant u, v \leqslant n$

算法分析

在边权为正的树 $T$，记 $x_T, y_T$ 为一组直径端点，因为距离 $T$ 中任意一个点最远的 $T$ 中的点是 $x_T$ 或 $y_T$，那么用一条边 $(u, v)$ 连接两棵树 $T_1, T_2$，$u \in T_1, v \in T_2$，对于新树 $T_1 \cup T_2$，新的直径端点一定是 $\{ x_{T_1}, y_{T_1}, x_{T_2}, y_{T_2}\}$ 中的两个。具体地，如果新直径不经过 $(u, v)$，那么其出自原直径；否则找到 $T_1$ 中距离 $u$ 最远的点和 $T_2$ 中距离 $v$ 最远的点作为直径端点，由上述性质得到这两个端点也出自四个原端点。

由此，只要能快速计算当前每颗树中任意两点的距离，就能借助记录每棵树中的直径端点来快速回答询问。但是由于强制在线，我们不能一次性完成预处理。每颗树 $T$ 任取一个根节点，通过倍增 $\operatorname{LCA}$ 和记录每个点的深度就能计算距离。加边 $(u, v)$ 合并 $T_1, T_2$ 时，根据启发式合并的思想，暴力搜索较小的树，更新其倍增和深度信息，就能在新树里快速查询距离了。

总的时间复杂度为 $\mathcal{O}(n\log n)$

代码实现

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;
using P = pair<int, int>;

struct UnionFind {
    vector<int> d, d1, d2;
    UnionFind(int n = 0): d(n, -1), d1(n), d2(n) {
        rep(i, n) d1[i] = i;
        rep(i, n) d2[i] = i;
    }
    int find(int x) {
        if (d[x] < 0) return x;
        return d[x] = find(d[x]);
    }
    bool unite(int x, int y) {
        x = find(x); y = find(y);
        if (x == y) return false;
        if (d[x] > d[y]) swap(x, y);
        d[x] += d[y];
        d[y] = x;
        return true;
    }
    bool same(int x, int y) {
        return find(x) == find(y);
    }
    int size(int x) {
        return -d[find(x)];
    }
    P getDiam(int x) {
        x = find(x);
        return P(d1[x], d2[x]);
    }
    void setDiam(int x, P diam) {
        x = find(x);
        tie(d1[x], d2[x]) = diam;
    }
};

int main() {
    cin.tie(nullptr) -> sync_with_stdio(false);

    int n;
    cin >> n;

    int lg = log2(n)+2;
    vector anc(n, vector<int>(lg));
    rep(i, n) anc[i] = vector<int>(lg, i);

    vector<int> dep(n);
    auto jump = [&](int x, int steps) {
        rep(i, lg) {
            if (steps>>i&1) x = anc[x][i];
        }
        return x;
    };
    auto lca = [&](int a, int b) {
        if (dep[a] < dep[b]) swap(a, b);
        a = jump(a, dep[a]-dep[b]);
        if (a == b) return a;
        for (int i = lg; i--;) {
            if (anc[a][i] != anc[b][i]) {
                a = anc[a][i];
                b = anc[b][i];
            }
        }
        return anc[a][0];
    };
    auto dist = [&](int a, int b) {
        int c = lca(a, b);
        return dep[a]+dep[b]-2*dep[c];
    };

    vector<vector<int>> to(n);
    auto dfs = [&](auto& f, int v, int p=-1) -> void {
        anc[v][0] = p;
        dep[v] = dep[p]+1;
        for (int i = 1; i < lg; ++i) {
            anc[v][i] = anc[anc[v][i-1]][i-1];
        }
        for (int u : to[v]) {
            if (u == p) continue;
            f(f, u, v);
        }
    };

    int ans = 0, now = 0;
    UnionFind uf(n);
    rep(i, n-1) {
        int a, b;
        cin >> a >> b;
        a ^= ans;
        b ^= ans;
        --a; --b;

        if (uf.size(a) < uf.size(b)) swap(a, b);

        to[a].push_back(b);
        to[b].push_back(a);

        P dv1 = uf.getDiam(a);
        P dv2 = uf.getDiam(b);
        vector<int> vs = {dv1.first, dv1.second, dv2.first, dv2.second};

        dfs(dfs, b, a);
        uf.unite(a, b);

        now -= dist(dv1.first, dv1.second);
        now -= dist(dv2.first, dv2.second);

        P diam;
        int d = 0;
        rep(i, vs.size())rep(j, i) {
            int nd = dist(vs[i], vs[j]);
            if (nd > d) {
                d = nd;
                diam = P(vs[i], vs[j]);
            }
        }
        uf.setDiam(a, diam);
        now += d;
        ans ^= now;
    }

    cout << ans << '\n';

    return 0;
}