1.前言

你是一枚486，无意间进入了动态规划的异世界……

从今天起，我们真是来是学习逢考必有的动态规划（dP)

那么，我们就先聊聊动态规划的基础和基本解题思路吧（顺带水一篇分享）

说了这么多，到底什么是动态规划呢？

动态规划（Dynamic Programming，DP），是求解决策过程最优化的过程。动态规划的应用极其广泛，包括工程技术、经济、工业生产、军事以及自动化控制等领域，并在背包问题、生产经营问题、资金管理问题、资源分配问题、最短路径问题和复杂系统可靠性问题等中取得了显著的效果 — —度娘

相信聪明小伙伴们看懂了这 $\overset{晦涩难懂}{通俗易懂}$的定义，那么——

动态规划，实际上就是“动态的规划”（我瞎下的定义），还不理解的话，继续往下看吧~

2.思想引入

咱们以例题来引入正题，以便读者食用
eg:斐波那契和他的不死兔子

wp1.已正常的思路，就会想到递归，之前络合物写过递归的总结（这里->传送门）这里不再阐述

wp2.一点优化

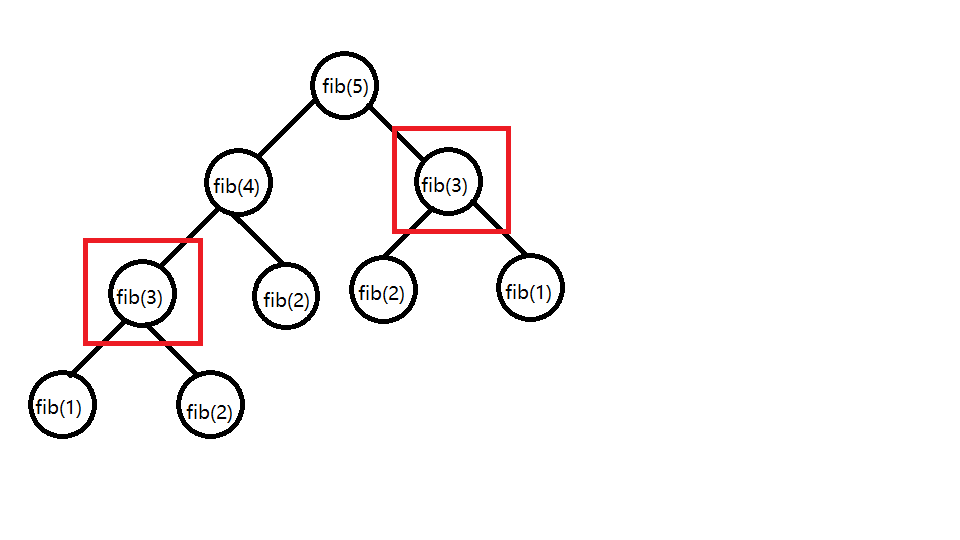
如图，我们可以看到，用递归的方法计算fib(5)，实际上重复计算了fib(3)的部分。这看起来并无大碍，但如果计算fib(10),fib(50),甚至是fib(100)呢？重复计算会倍增，时间复杂度也会倍增。
那么该怎么办呢？

$\color{#FF0000}{把已算过的fib存起来直接用呗！}$

代码如下：

#include<iostream>
using namespace std;
long long memo[100001]= {0};//存储空间
long long fibo(int n,long long* memo) {//递归进阶
    if(n==1||n==2) {
        return 1;
    }
    if(memo[n]!=0) return memo[n];
    else {
        memo[n]=fibo(n-1,memo)+fibo(n-2,memo);
        return memo[n];
    }
}

int main(){
    cout<<fibo(150,memo);//计算fib(150)的值
}

wp3.亿点优化（切入正题）

经过前两个例子，大家也可以清楚地体会到，要想计算$fib(n)$的值，计算$fib(n-1)+fib(n-2)$即可
所以$fibonacci$（放洋屁）的方程就出来了$fib(n)=fib(n-1)+fib(n-2)$
代码实现：

#include<iostream>
using namespace std;
int memo[101]={0};
int main(){
    memo[1]=1;
    memo[2]=1;//定义fib(1)和fib(2)为1
    int n;
    cin>>n;
    for(int i=3;i<=n;i++){
        memo[i]=memo[i-1]+memo[i-2];
    }
    cout<<memo[n];
}

有些小朋友可能会问了，这不就是递推吗？
没错，他就是递推

3.总结

以上呢就是动态规划的基本思路啦，总结一下呢就是：

1. 寻找规律（一定会有的啊喂）
2. 列出线性方程
3. 写出代码，然后AC

这听起来很简单，但是每一道动态规划的题规律，线性方程大几率不同，所以很令人头秃

那么以上就是今天的内容啦，Day1动态规划至此结束
感谢@[染染]的大力支持和帮助
拜拜啦(´▽`ʃ♡ƪ)