无符号整数、二进制补码
数字表示的底层逻辑:
计算机内部可以看成一个带子,带子被分成了好几段,每一段上都存放着不同的东西。
如下图所示:
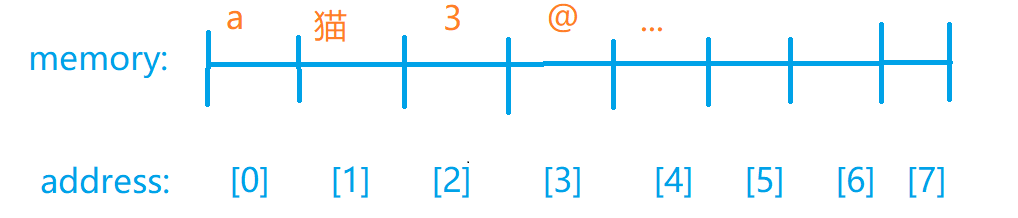
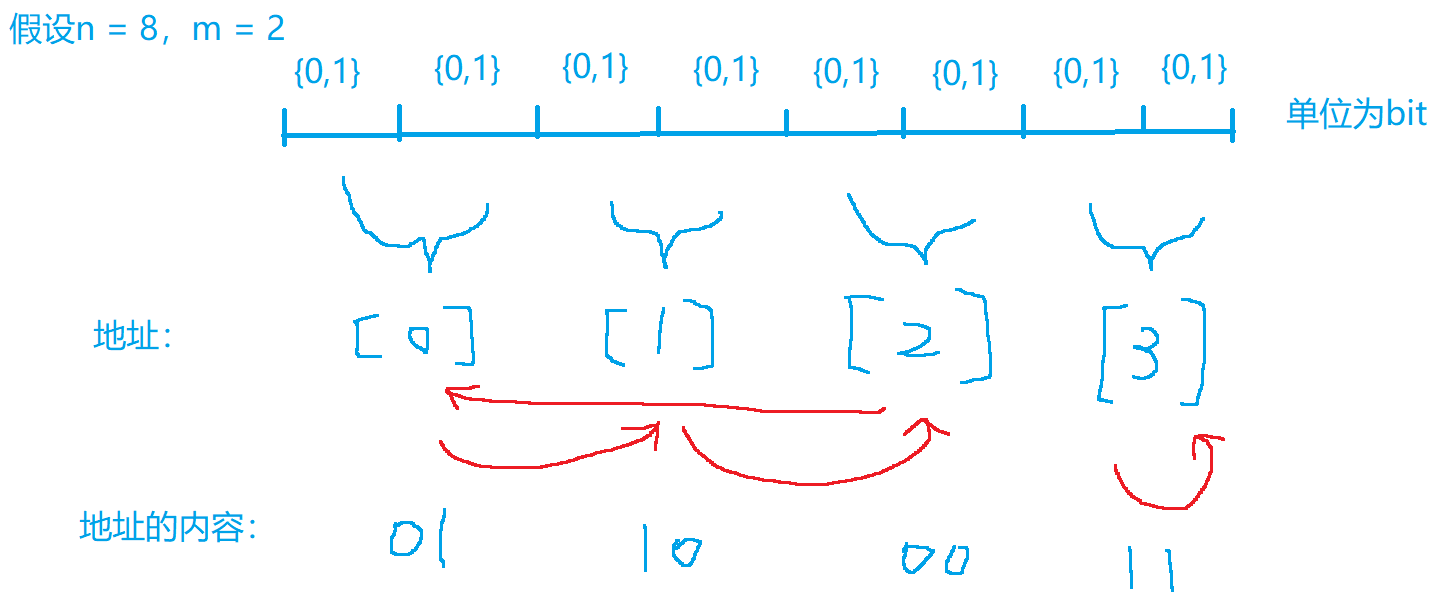
假设计算机内部一共有$n$个bit$\in{0,1}$,但是1bit只能表示${0,1}$。为了能一个地址指向的内存单元能表示更多东西同时提高检索能力,我们通常将m个bit作为一个块,每个块共同表示一个内容。
其中,有个重要结论:块数不能大于块的寻址能力,即$n/m <= 2^m$
下图是刚好$n/m=2^m$的情况,若n = 9,此时第9个bit无法被块寻找到。
十进制数、二进制数的本质
首先确定一个观念,我们日常使用的数字不是真正的数,而是一个符号序列。真正的数通过一层抽象才形成了我们常用的符号序列。
接下来看看这个抽象是怎么样的:
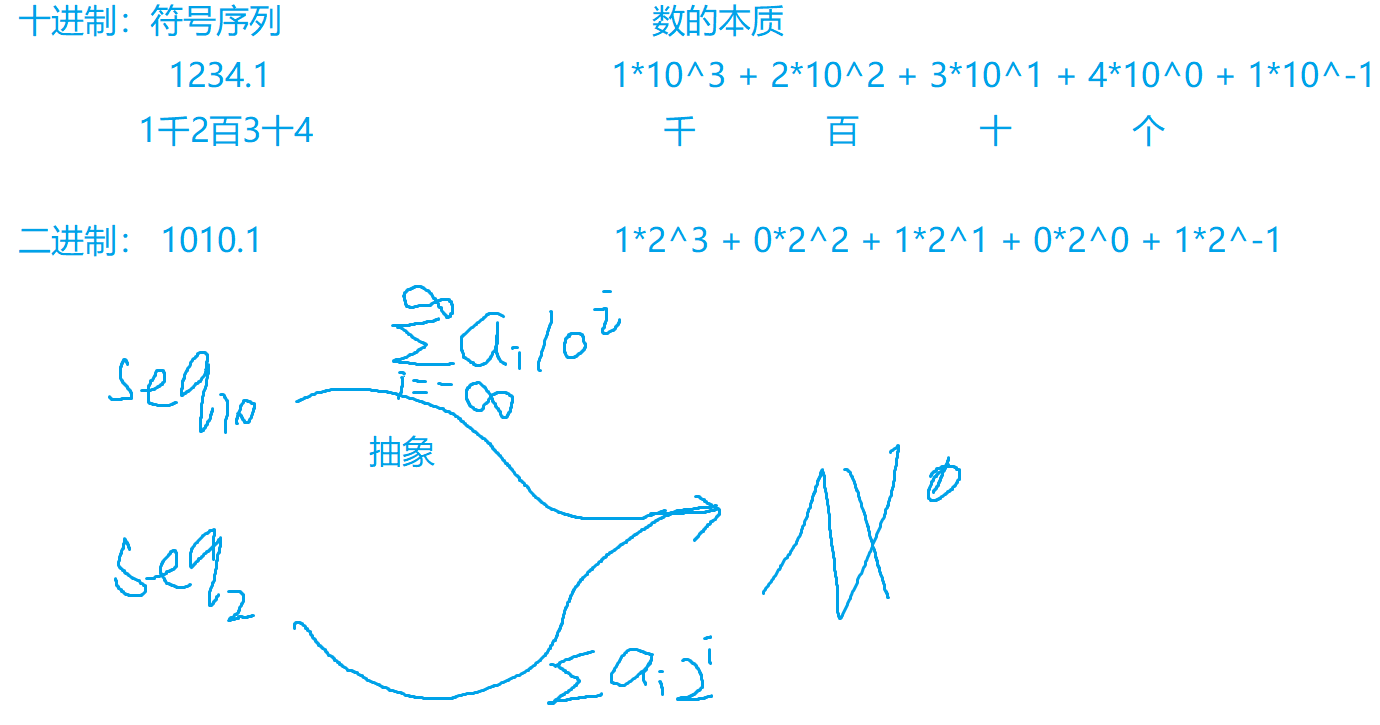
另外,我们可以惊奇的发现,二进制数和十进制数是一一对应的,并且二进制运算和十进制运算也是对应的,看如下举例:
$123 + 1 = 124 => 0001 0010 0011 + 0001 = 0001 0010 0100$
无符号整数、二进制补码
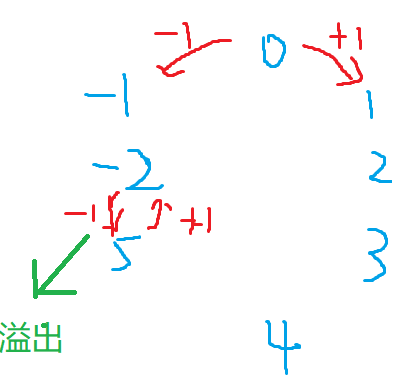
上面探讨的运算都是基于无穷位时得到的一些规律。在计算机底层往往是有限位。还是假设每个块一共m位。
具体区别看下图:
- 当$m=+\infty$时,此时代数结构为线性的
- 当$m < +\infty$时,此时代数结构为环形的,在数学上表现为取模运算。
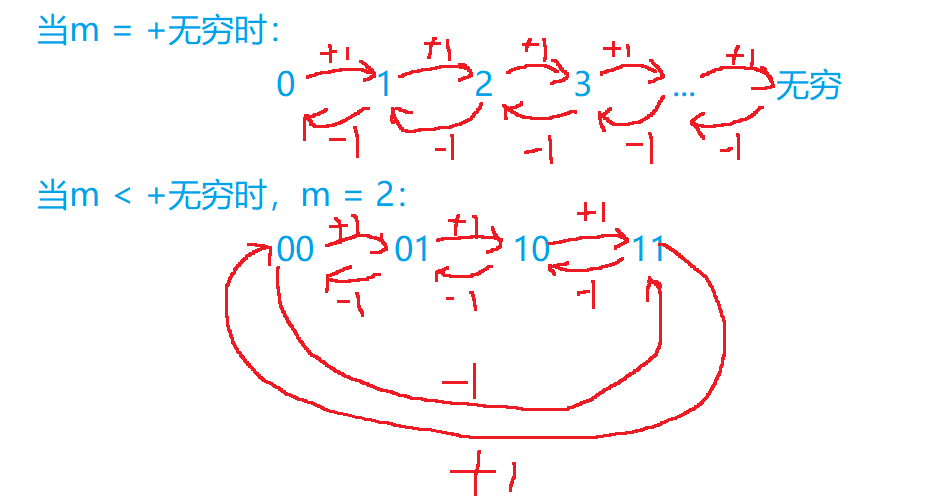
由此我们推出无符号数在计算机底层的存储逻辑本质上是个环形代数结构。而二进制补码是将可表示数的数量的一半拿来表示非负数,另一半拿来表示负数,为了实现这个目的,具体操作就是将溢出的位置旋转$Π$。补码表示范围是$-2^{m-1} < x < 2^{m-1} - 1$
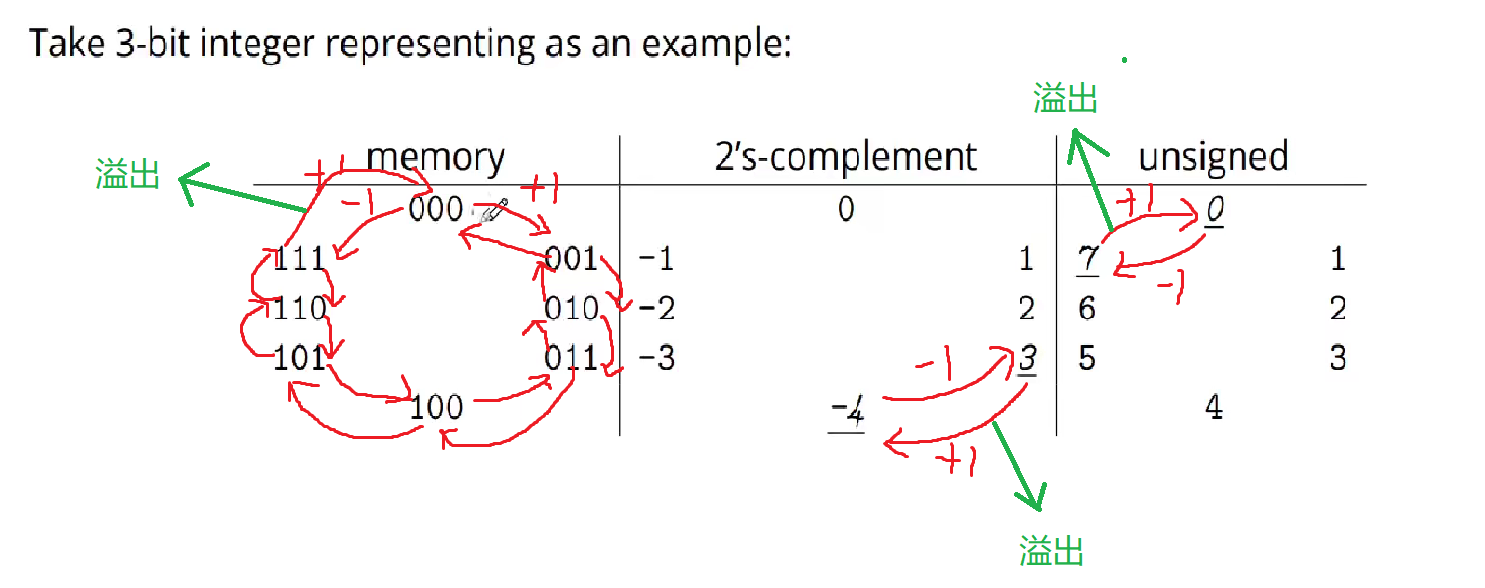
补充:
-
32位表示范围:-2147483648 ~ 2147483647
-
也可以将溢出位置旋转$3/2Π$,如图。但是负数个数比非负数少的多,这么表示意义不大。