一、什么时候考虑数位dp

当题目有以下特征时：

1.在某个区间
2.求满足一定条件下某些数的数量
3.这些条件可以转化为与数位有关的方法

二、思考方法

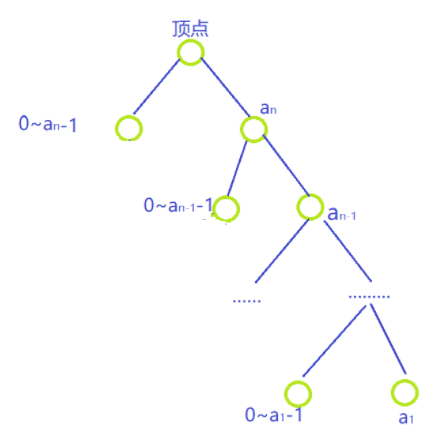
如图对于每一位，可分为两个集合
例如对第n位，可分为0~an-1,an（这样可以保证符合条件的数都在x范围内）.对于0~an-1可以预处理出来（init()函数），init()一般用dp。

1.求某个区间可用前缀和思想

例如：求在l~r的所有数. 可先求出0~r和0~l-1所有数，再用0~r的总数减去0~l-1即可。
现在就将问题转化为求0~x之间的数，即符合条件的数都小于x

2.大体思路：
例如：求符合条件的在0~x所有的数

1.先抠出x的每一位：
 vector<int> num;
    while(t) num.push_back(t % b), t /= b;
2.从高到低枚举x的每位，符合条件的数对应的位数一定满足 小于等于 x相对应的位数
for(int i = num.size() - 1; i >= 0; i --)
    {
        for(int j = last; j < num[i]; j ++)     //这里求的是上一位为x抠出的数
        res += f[i + 1][j];                 

        if(last > x) break;
        last = x;                       //存上一位的最大的数
        if(!i) res ++;                  //如果到底了，即x本身也算一种情况
    }

三、部分细节

1.实质是一种低复杂度的枚举
2.init()一般需用dp知识
3.用图理解每个节点的分类很重要
4.对于每一位（图的每个节点）分两种情况，当取0~an-1时，无论后面数怎么选，都满足小于x
当取an时，只能进入下一位，以此类推。