往期目录-> 传送门
————————————
1.本节导入
动态规划入门后,相信小伙伴们已经对动态规划有了一定的了解
那么,让我们来看看动态规有哪些的模板题型吧
动态规划一般可分为
线性动规,区域动规,树形动规,背包动规四类
那么我们就从比较简单的背包问题(我觉得)入手吧,毕竟不需要 树 等相关知识的说
2.背包问题
背包问题又分为01背包,完全背包,部分背包,多重背包
我们先来看看01背包和完全背包(因为比较水)
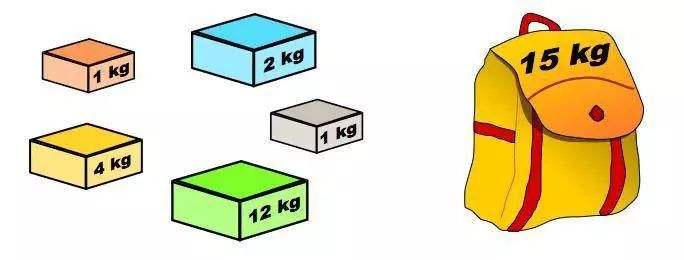
3. 01背包问题
问题概述:有 n 个物体,重量分别为 wi,价值为 vi,在总重量不超过容量 C 的情况下让总价值最高,
但不允许只取走部分物体,要拿走只能整个拿走。
这类问题有着比较固定的解法
像往常一样,我们还是以一道例题引入
01背包 (看完题回来啊喂——卑微作者的呐喊)
Day1时我们说到,动态规划的核心就是列方程,那么这类问题的方程是什么呢?先来看第一步
我们设置一个二维数组$a[101][101],横行用来存储空间,纵行用来存储价值,
当背包容量小于物品体积时,那么就无法存下这个物品,此时填0,如果能存下,填入价格
当背包储存空间为1时,此物品可以装下,那么就在格中填入它的价值,如图
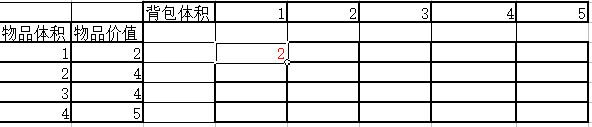
那么第一行就可以用这种方法填完,如图
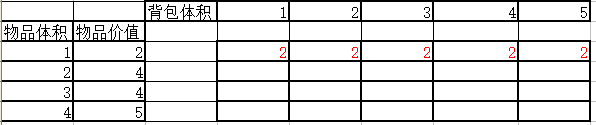
$\color{#FF0000}{那么,恭喜你完成了第一步}$
第二行,第三行到第n行的内容是较核心内容
来思考下,要放置第二个物品时,如何能保证物品能放入并且价值最大呢?
$\color{#FF0000}{做个比较呗!}$
来看,如果要放下第二个物品,那需要的空间就是$2+4=6$个空间,及$a[i-1][j-w[i]]$,i为含,j为列
再与$a[i-1][j]$和$a[i-1][j-w[i]+V[i]$(v[i]为此物品价格)做对比
如果$a[i-1][j-w[i]+V[i]>a[i-1][j]$,填入$a[i-1][j-w[i]+V[i]$,否则把$a[i-1][j]$的值托下来,如图
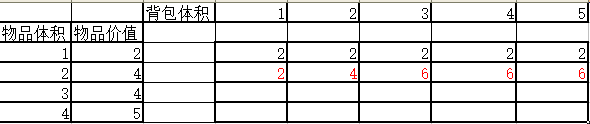
以此类推,最终结果为
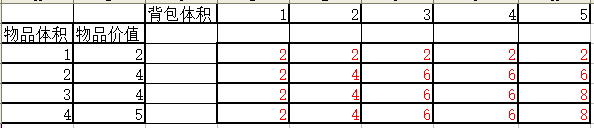
此时,最终结果就为最右下角的结果:8,直接输出$a[5][4]$即可
代码实现
#include<iostream>
using namespace std;
int w[101],v[101],a[101][101];//定义w[i],v[i]和二维数组
int n,c;
int main(){
cin>>c>>n;
for(int i=1;i<=c;i++){
cin>>w[i]>>v[i];
}
for(int i=1;i<=c;i++){
for(int j=1;j<=n;j++){
if(w[i]<=j){//如果能装下
a[i][j]=max(a[i-1][j],a[i-1][j-w[i]]+v[i]);//比较大小
}
else{
a[i][j]=a[i-1][j];
}
}
}
cout<<a[c][n];//输出右下角的数
}
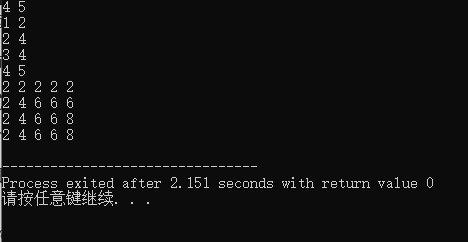
如果直接输出数组,可以看到与上述图片结果相同
4.01背包问题一维数组优化
上面介绍了二维数组的01背包,但有些苛刻的题目(没遇到过…)给你卡的死死的,那么这时就需要一点优化
这里举个简单的例子说明为什么他能优化空间
考试要考数学、语文、英语、物理、化学、生物六科
每考完一科,就扔掉一科的书
这样背包里的空间不就省出来了吗?
对于我们的一维数组也是一样
算完一组,扔掉一组,所以空间就生出来了。
大家想想,如何才能把一个二维数组简化为一维数组,或者说删去二维数组的行还是列呢?
显而易见,答案是行
但是,这又涉及到了一个问题,数据被篡改
在使用二位背包的时候可以注意到,后面的结果是根据前面计算出的结果所来,所以在计算时后面的数据就被篡改了,那怎么办?
$\color{#FF0000}{倒序输出呗!}$
代码如下:
#include<iostream>
using namespace std;
int w[1005],v[1001],a[1001],n,c;
int main(){
cin>>c>>n;
for(int i=1;i<=c;i++){
cin>>w[i]>>v[i];
}
for(int i=1;i<=c;i++){
for(int j=n;j>=1;j--){//倒序输出
if(w[i]<=j){
a[j]=max(a[j],a[j-w[i]]+v[i]);
}
}
}
cout<<a[n];
}
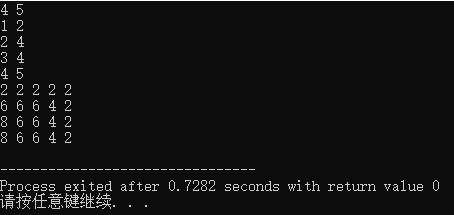
直接打表的话可以看到就是倒序输出的结果
5.完全背包
同样,先来看例题
刚才我们在讲一维01背包时说到,后面的数据由前面的数据所来,所以数据会被篡改
而这所谓的数据篡改,实际上就是……
$\color{#FF0000}{可以无限次取一样东西的另一种说法}$
所以说正序输出就是答案
代码如下:
#include<iostream>
using namespace std;
int w[1005],v[1001],a[1001],n,c;
int main(){
cin>>c>>n;
for(int i=1;i<=c;i++){
cin>>w[i]>>v[i];
}
for(int i=1;i<=c;i++){
for(int j=1;j<=n;j++){//正序输出
if(w[i]<=j){
a[j]=max(a[j],a[j-w[i]]+v[i]);
}
}
}
cout<<a[n];
}
读者一定要区分倒序输出和正序输出导致的结果的不同,分别对应01背包和完全背包
6.后记
欸……终于肝完了……三个小时就这点东西……(不过还挺有成就感的说)
总之下周本络合物就要期末考试,所以部分背包和多重背包等寒假再更吧(也不一定哈哈)
那么这期就到这里了,我们下期再见,拜拜ヾ(•ω•`)o


