1.求解一个数的约数

试除法：
时间复杂度为O(sqrt(n))

//试除法求约数
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
vector<int>get_yueshu(int x){
    vector<int>res;
    for(int i=1;i<=x/i;i++){
        if(x%i==0){           //只枚举小的那个约数
            res.push_back(i);
            if(i!=x/i){       //如果大的约数和小的约数不一样，就存入数组中，否则不存入
                res.push_back(x/i);
            }
        }
    }
    sort(res.begin(),res.end());
    return res;
}
int main(){
    int n;

    cin>>n;
    int x;
    while(n--){
        cin>>x;
        vector<int>T=get_yueshu(x);
        for(auto t:T){
            cout<<t<<' ';
        }
        cout<<endl;
    }
    return 0;
}

2.求解约数的个数
X=p1^a1p2^a2…………pk^ak;
对于每一个pi^ai都有：
pi^0、pi^1…………pi^ai个质因子，所以质因子的个数ans=(0+1+2……+ai)=ai+1
所以X的约数有(a1+1)(a2+1)…………(ak+1)个
其实就是排列组合，看这些质因子有多少中排列情况
举例：
218=36，2=2^1, 18=2^13^2
所以36=2^23^2;
36的约数为 (2+1)*(2+1)=9,即 1 2 3 4 6 9 12 18 36

代码：

对于该题使用了没有使用过的map，详情： [map函数使用方法](https://blog.csdn.net/weixin_43828245/article/details/90214494) 
函数中不能有重复的键，但是可以有相同的键值，并且在该题目的插入中，因为质因子i不确定
所以选择primes[i]++的方式，每存入一个键为i，键值就++

#include<iostream>
#include<map>
using namespace std;
long long res=1;
const int N=1e9+7;
map<int,int>primes;

int main(){

    int n;
    cin>>n;
    while(n--){
        int x;
        cin>>x;
        for(int i=2;i<=x/i;i++){
            if(x%i==0){
                int k=0;
                while(x%i==0){
                    x=x/i;
                    primes[i]++;
                //primes.insert(pair<int,int>(i,++k));
                    }
            }
        }
        if(x>1)
        primes[x]++;
    }
    for(map<int,int>::iterator t=primes.begin();t!=primes.end();t++){
        res=res*(t->second+1)%N;
    }
    cout<<res;
    return 0;
}

3.求解一个数的约数和
在这里学到了用 auto去遍历map函数十分的简便
另外一个就是秦九韶算法，真的绝了
关于这个算法在22年寒假每一一题的笨拙的手指中听y总讲过，那会就感觉很精妙
但是没有深入去研究，今天在听约数和的时候再次惊讶秦九韶算法的精妙
这里：借用大佬的讲解
如果 N=p1^c1∗p2^c2∗…∗pk^ckN=p1^c1∗p2^c2∗…∗pk^ck
约数个数：(c1+1)∗(c2+1)∗…∗(ck+1)(c1+1)∗(c2+1)∗…∗(ck+1)
约数之和： (p1^0+p1^1+…+p1^c1)∗…∗(pk^0+pk^1+…+pk^ck)

算约数和的话需要求解出每一个质因子从其指数为0一直到他在x中出现的最大次数的和
然后各个相乘。
我的思路是利用pow()函数，代码如下：

 /*for(map<int,int>::iterator t=primes.begin();t!=primes.end();t++){
        int f=t->first;
        long long res=0;
        for(int i=0;i<=t->second;i++){
            res+=pow(f,i)%N;     //N=1e9+7

        }
        sum=sum*res%N;
    }
    cout<<sum;
    */

然后数小的时候结果正确，但是当数大的时候就会出现问题，原因在于
1.pow()函数的返回值是double类型而非int类型
2.他这个mod 1e9+10这里在式子中会出现问题所以不管怎样变化他就是有问题
通过看别的伙伴的思路，他们提出使用等比数列求和的方法也出现了问题
因为不知道是先mod 1e9+10还是先加再mod,这样精度啥的会出现问题，
然后看视频讲解时，y总用了秦九韶算法解决这个问题，简直目瞪口呆
t=t∗p+1
t=1
t=p+1
t=p2+p+1
……
t=pb+pb−1+…+1
太神奇了

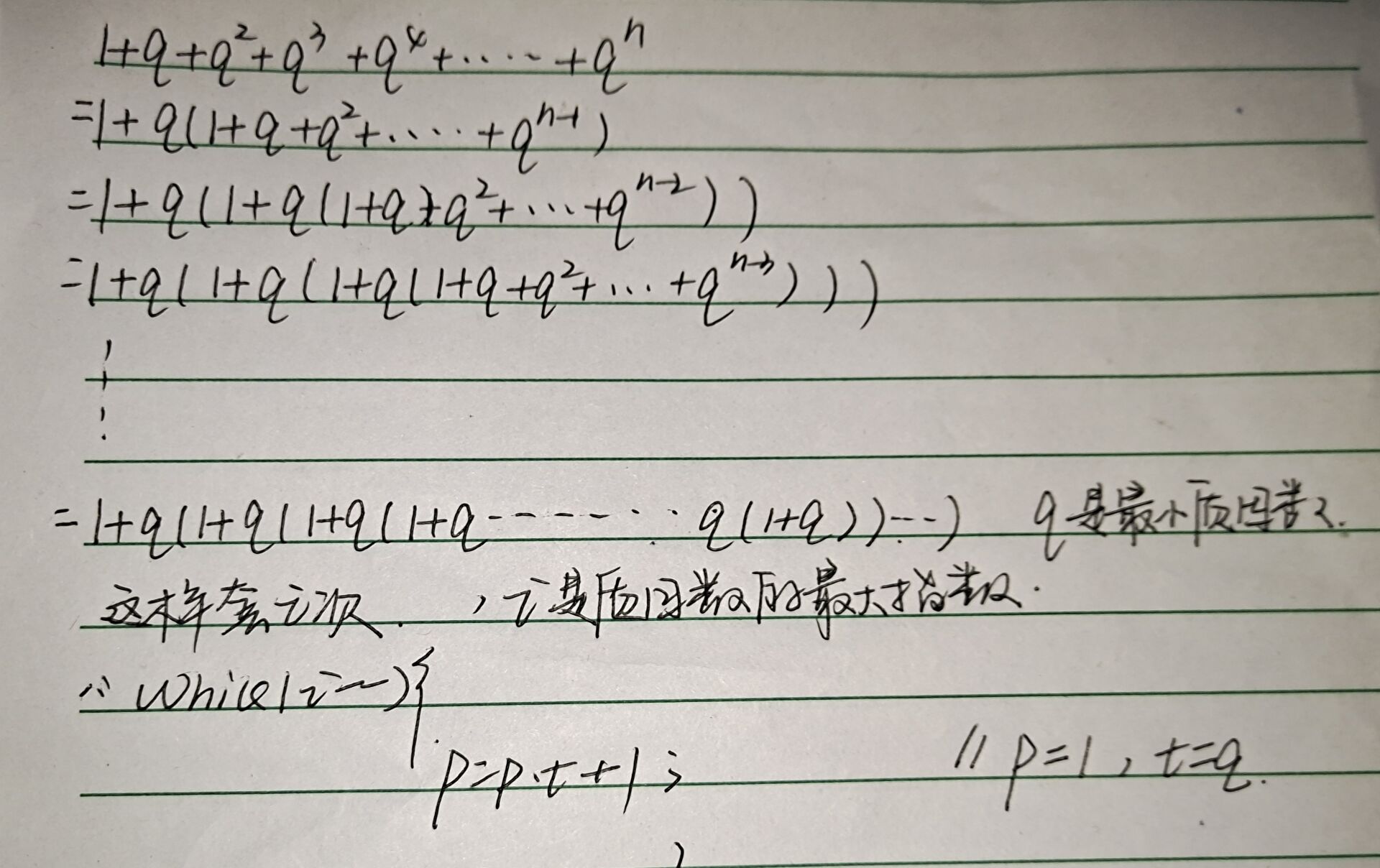
还有b进制转化为十进制的题目
代码：

int get(string s,int b){
//b进制函数转化为十进制
    int x=0;
    int i=0;
   /* for(auto c: s){
         x=x*b+c-'0';
    }*/
    while(i<s.size()){
        x=x*b+s[i]-'0';
        i++;

    }
    return x;
}

就是一串式子进行化简成这个样子，找规律确定各个值
好了上代码吧！

#include<iostream>
#include<map>
#include<vector>
#include<cmath>
using namespace std;
const int N=1e9+7;
map<int,int>primes;
int main(){

    int n;
    cin>>n;
    while(n--){
        int x;
        cin>>x;
        for(int i=2;i<=x/i;i++){
            while(x%i==0){
                x=x/i;
                primes[i]++;
            }
        }
        if(x>1){
            primes[x]++;
        }
    }

    long long res=1;
    for(auto t:primes){        //用auto遍历，convenience
        int p=t.first;
        int d=t.second;
        long long sum=1;
        while(d--){
            sum=(sum*p+1)%N;

        }
        res=res*sum%N;
    }
    cout<<res;
    return 0;
}

4.欧几里得求最大公约数

直呼精辟啊！
证明如下：
有数字a,b;那么a、b的最大公约数等价于(b,a mod b)，注意顺序，就是大的那一方在第一个数的位置
小的那一方在第二个数的位置，如此循环往复直至第二个数为0，此时结束，第一个数也就是两者的最大公约数
为什么上边两个式子是等价的呢，因为
假设d是a,b的最大公约数，d|a, d|b ,那么d|ax+by
a mod b=a-kb,k是a/b下取整，成立
从左往右推：因为d|a, d|b，所以d|a-kb
从右往左推：因为d|a-kb ，d|b 现证明：d|a :
d|a-kb +k*b = d|a 成立

代码：

#include<iostream>
using namespace std;
int gcd(int a,int b){
    if(b!=0){
        return gcd(b,a%b);
    }
    else{
        return a;
    }
}
int main(){

    int n;
    cin>>n;
    int a,b;
    while(n--){
        cin>>b>>a;
        cout<<gcd(a,b)<<endl;
    }
    return 0;
}