0216 算法基础课背包问题思考
动态规划问题总体从两个方面进行思考:
- 状态表示
- 状态计算
01背包问题
题目描述
有 $N$ 件物品和一个容量是 $V$ 的背包。每件物品只能使用一次。
第 $i$ 件物品的体积是 $v_i$,价值是 $w_i$。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行两个整数,$N$,$V$,用空格隔开,分别表示物品数量和背包容积。
接下来有 $N$ 行,每行两个整数 $v_i$,$w_i$,用空格隔开,分别表示第 $i$ 件物品的体积和价值。
样例
输入
4 5
1 2
2 4
3 4
4 5
输出
8
分析
算法1——二维
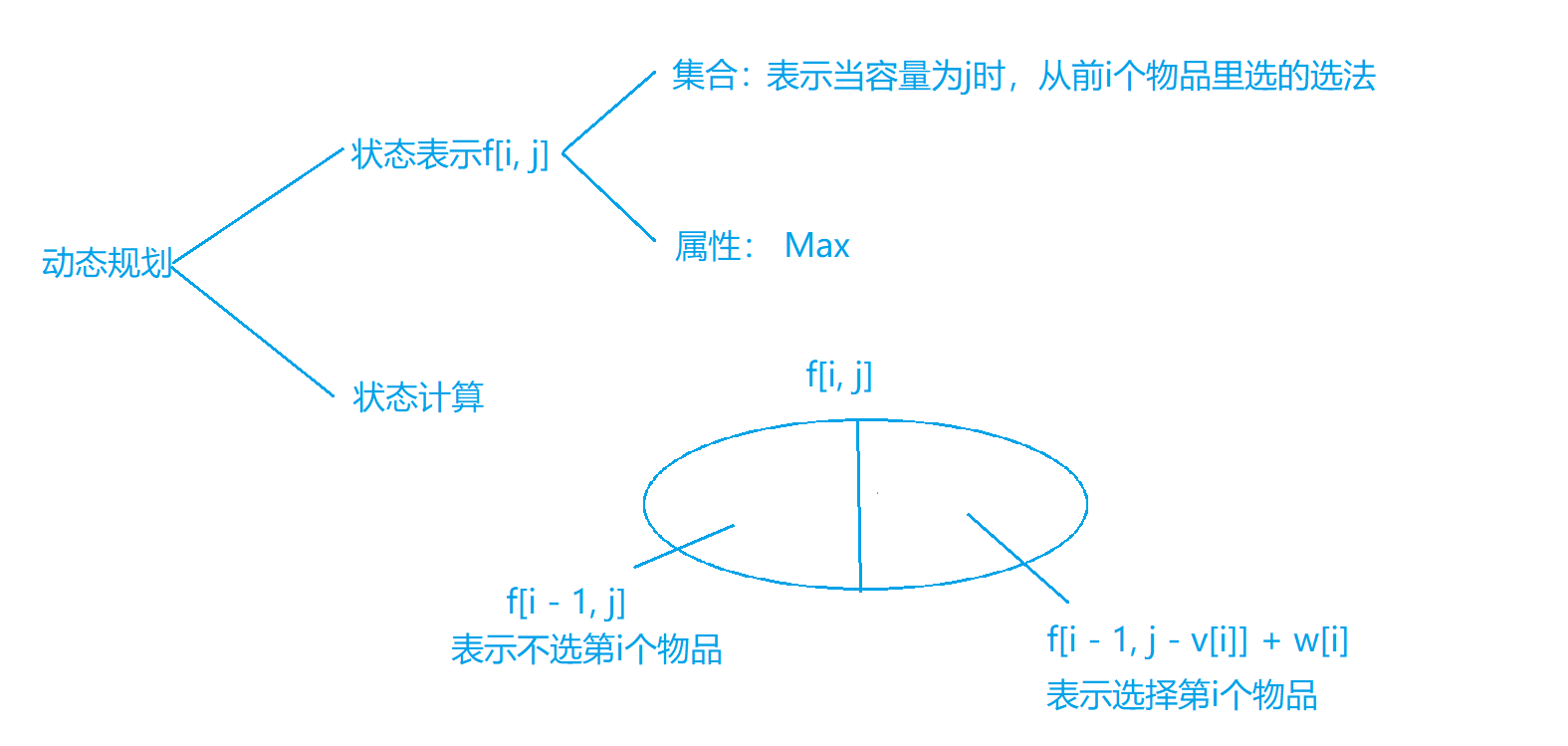
状态分析
(1)状态f[i][j]定义:前 $i$ 个物品,背包容量 $j$ 下的最优解(最大价值)
- 根据状态计算的分析我们知道,当前状态的计算依赖之前状态的计算,所以我们需要给初始的状态进行赋值,即
f[0][0] = 0(容量为0是,最大值是0)。
(2)当j < v[i]时,因为第$i$个物品不能放入背包,所以f[i][j] = f[i - 1][j]
(3)当j >= v[i]时,我们就进行决策,看是否选第 $i$ 个物品不选
f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i])
时间复杂度
$O(n^2)$
参考文献
C++ 代码
# include <iostream>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N][N];
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i ++ )
cin >> v[i] >> w[i];
for (int i = 1; i <= n; i ++ )
for (int j = 0; j <= m; j ++ )
{
f[i][j] = f[i - 1][j];
if (v[i] <= j) f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
}
cout << f[n][m] << endl;
return 0;
}
算法2——一维
状态分析
将状态f[i][j]优化到一维f[j]
(1)为什么可以进行优化变形?
我们根据上面的分析可以知道当前状态需要依赖之前的状态的计算,即计算前$i$个物品是需要用到前$i - 1$个物品的值。但是,当第$i$个计算完成之后,我们无须保存$i - 1$层的值了。因为题目求得是f[n][m],所以只需要保存最后一层的值即可。
(2)如何理解f[j]的含义
当第一层循环到第$i$层时,f[j]就表示前$i$个物品,容量为$j$下的最大价值。
(3)为什么第二层循环范围不是$0–m$?
根据二维状态的分析我们知道,当j < v[i]时,f[i][j] = f[i - 1][j],当我们用一维表示时,当第i层循环中未更新 f[j] 之前, f[j] 保存的就是$i-1$状态下$f$的值,所以可以省去这个步骤。
等价代码
for (int i = 1; i <= n; i ++ )
for (int j = m; j >= 0; j -- )
{
f[j] = f[j];
if (j >= v[i])
f[j] = max(f[j], f[j - v[i]] + w[i]);
}
(4)为什么第二层循环要逆序进行?
这个问题和第三个问题中讲到的也有关系,当我们计算当前f[j](f[i][j])是需要用到上一状态的f[j - v[i]](f[i - 1][j]),如果我们正序循环,那么上一状态的f[j - v[i]](f[i - 1][j])会被更新为当前状态的f[j - v[i]](f[i][j]),而我们又没有存储上个状态的f[j - v[i]](f[i - 1][j]),所以我们要逆序去求解。
举个例子:
当我们需要计算前$4$个物品的f[4][j]的时候,我们需要f[3][j - v[4]]的值,第3层结束的时候,f[j - v[i]]存放的就是f[3][j - v[4]]的数值。当进入第$4$层循环,$j$正序循环的话,f[j - v[i]]就会先于f[j]被更新为f[4][j - v[4]],所以当计算f[4][j]的数值是,应该用f[3][j - v[i]]的值,但是此时f[j - v[i]]存放的是f[4][j - v[4]]。
时间复杂度
$O(n^2)$
C++ 代码
# include <iostream>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N];
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i ++ )
cin >> v[i] >> w[i];
for (int i = 1; i <= n; i ++ )
for (int j = m; j >= v[i]; j -- )
{
f[j] = max(f[j], f[j - v[i]] + w[i]);
}
cout << f[m] << endl;
return 0;
}
完全背包问题
题目描述
有 N 种物品和一个容量是$ V$ 的背包,每种物品都有无限件可用。
第 $i$种物品的体积是 $v_i$,价值是 $w_i$。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行两个整数,$N$,$V$,用空格隔开,分别表示物品数量和背包容积。
接下来有 $N$ 行,每行两个整数 $v_i$,$w_i$,用空格隔开,分别表示第 $i$ 件物品的体积和价值。
样例
输入
4 5
1 2
2 4
3 4
4 5
输出
10
分析
算法1——基础二维
状态分析
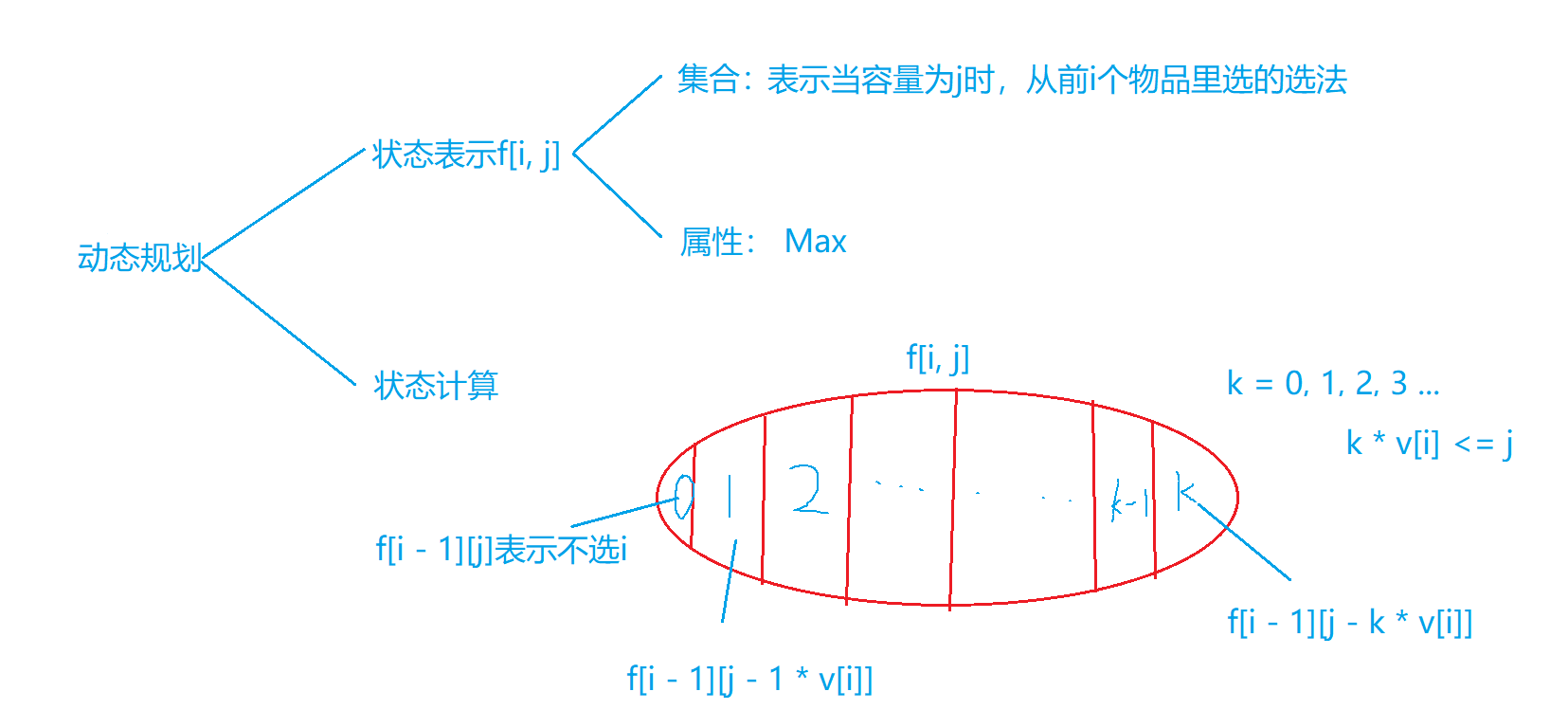
(1)状态f[i][j]定义:前 $i$ 个物品,背包容量 $j$ 下的最优解(最大价值)
(2)以选择第i个物品的数量为划分集合的依据, 当 k * v[i] <= j 前提下
f[i][j] = max(f[i-1][j-0*v[i]], f[i-1][j-1*v[i]] + w[i], f[i-1][j-2*v[i]]+2*w[i], ... ,f[i-1][j-k*v[i]]+k*w[i])
C++ 代码
# include <iostream>
# include <cstring>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N][N];
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i ++ )
cin >> v[i] >> w[i];
for (int i = 1; i <= n; i ++ )
for (int j = 0; j <= m; j ++ )
for (int k = 0; k * v[i] <= j; k ++ )
{
f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
}
cout << f[n][m] << endl;
return 0;
}
算法2——优化二维
为什么可以优化
根据前面的分析我们知道:
f[i][j] = max(f[i-1][j-0*v[i]], f[i-1][j-1*v[i]]+w[i], f[i-1][j-2*v[i]]+2*w[i], ... ,f[i-1][j-k_1*v[i]]+k_1*w[i])
$k_1 * v[i] <= j$
f[i][j - v[i]] = max(f[i-1][j-v[i]], f[i-1][j-v[i]-1*v[i]]+w[i], ... ,f[i-1][j-v[i]-k_2*v[i]])+k_2*w[i]
$k_2 * v[i] <= j - v[i]$
所以$k_2 + 1 == k_1$
即f[i-1][j-k1 × v[i]]) = f[i-1][j-v[i]-k1 × v[i]])
所以f[i][j] = max(f[i-1][j], f[i][j - v[i]]+ w[i])
C++代码
# include <iostream>
# include <cstring>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N][N];
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i ++ )
cin >> v[i] >> w[i];
for (int i = 1; i <= n; i ++ )
for (int j = 0; j <= m; j ++ )
{
f[i][j] = f[i - 1][j]; //表示一个也不选
if (v[i] <= j) f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);
}
cout << f[n][m] << endl;
return 0;
}
算法3——一维
状态表示
和01背包表达的意思是一样的
但是要解释一下为什么此时正序没问题
f[i][j] = max(f[i-1][j], f[i][j - v[i]]+ w[i])
当计算第 $i$ 层是f[j]时,需要用 $i-1$ 层的f[j]和$i$层的f[j - v[i]],所以我们要先把第 $i - 1$ 层的f[j - v[i]]更新为第 $i$ 层的f[j - v[i]]
C++代码
# include <iostream>
# include <cstring>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N];
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i ++ )
cin >> v[i] >> w[i];
for (int i = 1; i <= n; i ++ )
for (int j = v[i]; j <= m; j ++ )
{
f[j] = max(f[j], f[j - v[i]] + w[i]);
}
cout << f[m] << endl;
return 0;
}
多重背包问题 I
题目描述
有 $N$ 种物品和一个容量是 $V$ 的背包。
第 $i$ 种物品最多有 $s_i$ 件,每件体积是 $v_i$,价值是 $w_i$。
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。
输出最大价值。
输入格式
第一行两个整数,$N,V$,用空格隔开,分别表示物品种数和背包容积。
接下来有 $N$ 行,每行三个整数 $v_i,w_i,s_i$,用空格隔开,分别表示第 $i$ 种物品的体积、价值和数量。
样例
输入
4 5
1 2 3
2 4 1
3 4 3
4 5 2
输出
10
算法
分析
多重背包和完全背包不同之处在于每种物品的个数有限
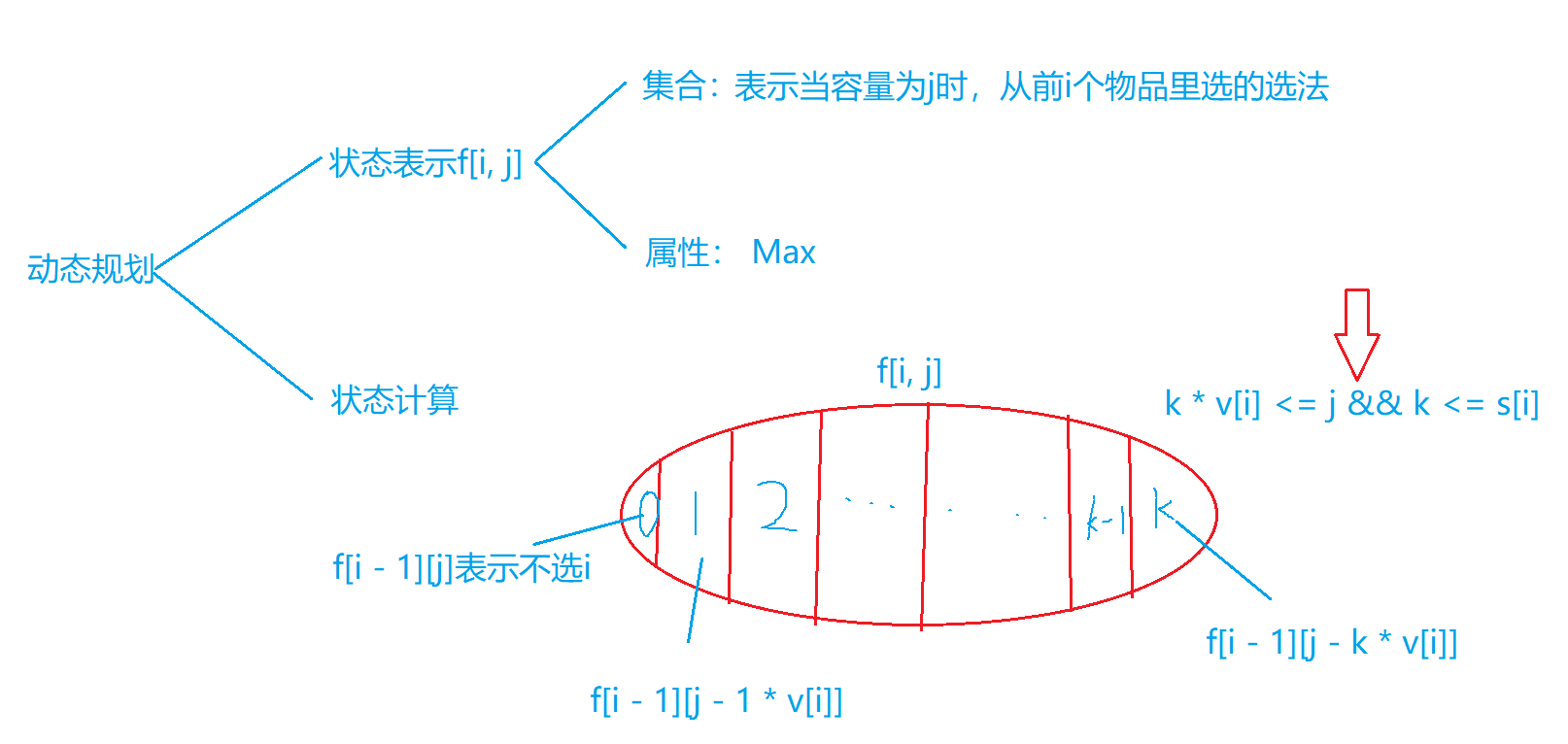
时间复杂度
$O(n^3)$
C++ 代码
# include <iostream>
# include <cstring>
using namespace std;
const int N = 110;
int n, m;
int v[N], w[N], s[N];
int f[N][N];
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i ++ )
cin >> v[i] >> w[i] >> s[i];
for (int i = 1; i <= n; i ++ )
for (int j = 0; j <= m; j ++ )
for (int k = 0; k <= s[i] && k * v[i] <= j; k ++ )
f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
cout << f[n][m] << endl;
return 0;
}
多重背包问题 II
题目描述
同多重背包问题 I
算法
分析
(1)I 和 II 不同之处在哪里
数据范围不同,当数据范围较大的时候,I的时间复杂度太高
(2)能不能参考完全背包一样进行优化?
能否像完全背包一样找到f[i][j] 和 f[i][j - v[i]]的关系

不能!
(3)那应该如何优化?
先思考为什么时间复杂度那么大。因为我们在第三层循环要一次枚举选i种物品的数量
介绍一个二进制优化的方法
原理:任何一个数都可以用其他更小的数进行表示
举例:如果我们要枚举1-64的话,正常我们一次枚举
但是如果我们进行二进制优化的话,我们对 1 2 4 8 16 32 进行组合可以表示1-63 对 1 1 2 4 8 16 32 进行组合便可以表示1-64 这样把复杂度从$O(n)$ -> $O(logn)$
(4)如何实现
将多重背包问题转换为01背包问题
假设有一组商品,一共有11个。
现在,如果我们把这11个商品分别打包成含商品个数为1个,2个,4个,4个(分别对应0001,0010,0100,0100)的四个”新的商品 “, 将问题转化为01背包问题,对于每个商品,我们都只枚举一次,那么我们只需要枚举四次 ,就可以找出这含组商品的最优解。 这样就大大减少了枚举次数。
参考
C++ 代码
# include <iostream>
using namespace std;
const int N = 12010, M = 2010;
int n, m;
int v[N], w[N];
int f[M];
int main()
{
cin >> n >> m;
int cnt = 0;
for (int i = 1; i <= n; i ++ )
{
int a, b, s;
cin >> a >> b >> s;
int k = 1;
while (k <= s)
{
cnt ++;
v[cnt] = a * k;
w[cnt] = b * k;
s -= k;
k *= 2;
}
if (s > 0)
{
cnt ++;
v[cnt] = a * s;
w[cnt] = b * s;
}
}
n = cnt;
for (int i = 1; i <= n; i ++ )
for (int j = m; j >= v[i]; j -- )
f[j] = max(f[j], f[j - v[i]] + w[i]);
cout << f[m] << endl;
return 0;
}
分组背包问题
题目描述
有 $N$ 组物品和一个容量是 $V$ 的背包。
每组物品有若干个,同一组内的物品最多只能选一个。
每件物品的体积是 $v_{ij}$,价值是 $w_{ij}$,其中 $i$ 是组号,$j$ 是组内编号。
求解将哪些物品装入背包,可使物品总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行有两个整数 $N,V$,用空格隔开,分别表示物品组数和背包容量。
接下来有 $N$ 组数据:
每组数据第一行有一个整数 $S_i$,表示第 $i$ 个物品组的物品数量;
每组数据接下来有 $S_i$ 行,每行有两个整数 $v_{ij},w_{ij}$,用空格隔开,分别表示第 $i$ 个物品组的第 $j$ 个物品的体积和价值;
样例
输入
3 5
2
1 2
2 4
1
3 4
1
4 5
输出
8
算法1——二维
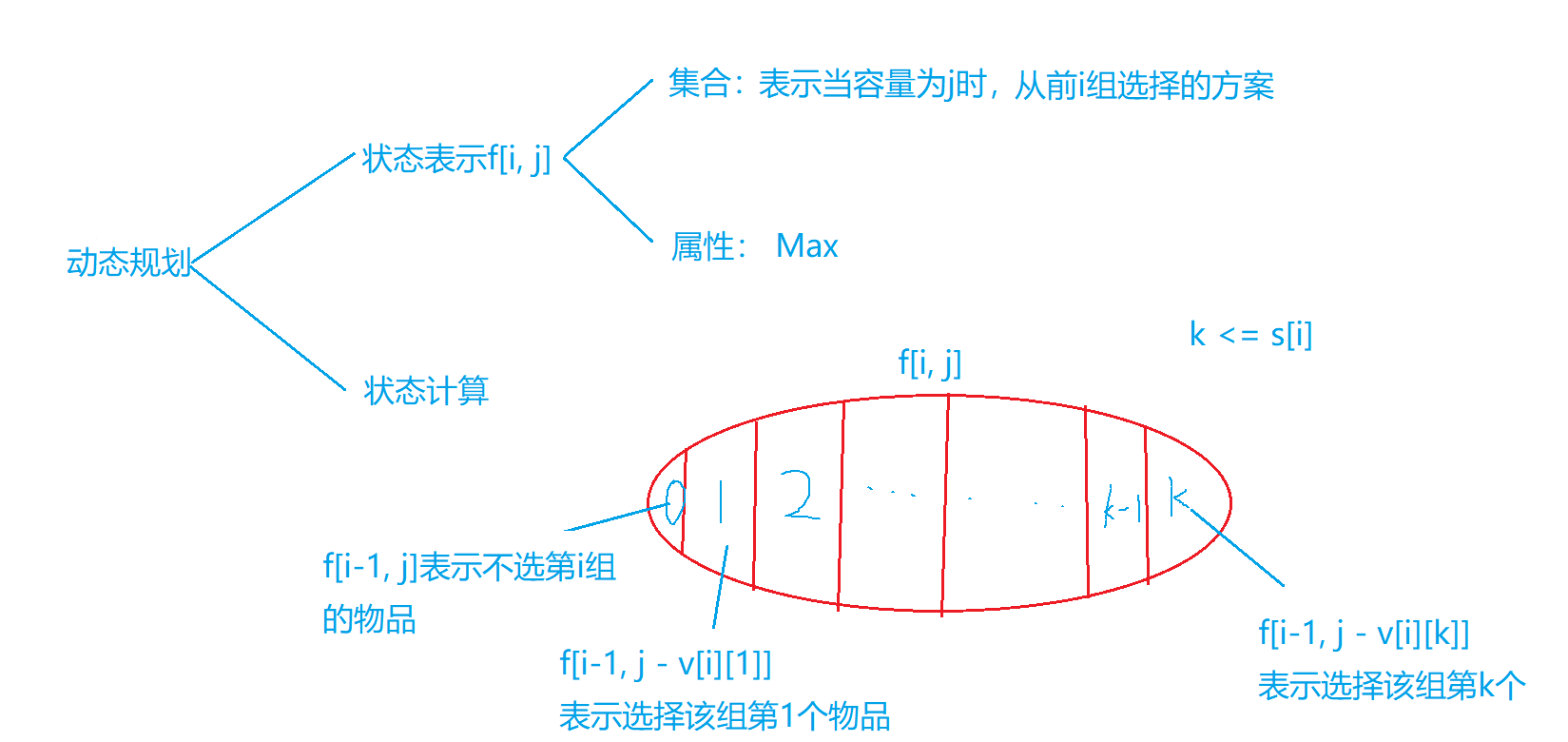
分析
C++ 代码
# include <iostream>
# include <cstring>
using namespace std;
const int N = 110;
int n, m;
int v[N][N], w[N][N], s[N];
int f[N][N];
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i ++ )
{
cin >> s[i];
for (int j = 1; j <= s[i]; j ++ )
cin >> v[i][j] >> w[i][j];
}
for (int i = 1; i <= n; i ++ )
for (int j = 0; j <= m; j ++ )
{
f[i][j] = f[i - 1][j]; //对应不选择第i组的元素
for (int k = 1; k <= s[i]; k ++ ) //k表示的不是数量,是选择第i组的第几个物品
{
if (v[i][k] <= j) f[i][j] = max(f[i][j], f[i - 1][j - v[i][k]] + w[i][k]);
}
}
cout << f[n][m] << endl;
return 0;
}
算法2——一维
分析
同前面的优化一样,从二维到一维
注意:
f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i][k]] + w[i][k]); $k = 1,2,…,s[i]$
j 要逆序 循环,但是因为该组每个物品的v不一定相同,所以m-0,不能省去0-v-1
C++ 代码
# include <iostream>
# include <cstring>
using namespace std;
const int N = 110;
int n, m;
int v[N][N], w[N][N], s[N];
int f[N];
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i ++ )
{
cin >> s[i];
for (int j = 1; j <= s[i]; j ++ )
cin >> v[i][j] >> w[i][j];
}
for (int i = 1; i <= n; i ++ )
for (int j = m; j >= 0; j -- )
{
for (int k = 1; k <= s[i]; k ++ )
{
if (v[i][k] <= j) f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
}
}
cout << f[m] << endl;
return 0;
}


题友前来拜读
贴贴!