一维前缀和
S[i] = a[1] + a[2] + … a[i]
a[l] + … + a[r] = S[r] - S[l - 1]

(1)离散化区间和

假定有一个无限长的数轴，数轴上每个坐标上的数都是 0。

现在，我们首先进行 n 次操作，每次操作将某一位置 x 上的数加 c。

接下来，进行 m 次询问，每个询问包含两个整数 l 和 r，你需要求出在区间 [l,r] 之间的所有数的和。

输入格式
第一行包含两个整数 n 和 m。

接下来 n 行，每行包含两个整数 x 和 c。

再接下来 m 行，每行包含两个整数 l 和 r。

输出格式
共 m 行，每行输出一个询问中所求的区间内数字和。

数据范围
−109≤x≤109,
1≤n,m≤105,
−109≤l≤r≤109,
−10000≤c≤10000
输入样例：
3 3
1 2
3 6
7 5
1 3
4 6
7 8
输出样例：
8
0
5
难度：简单
时/空限制：2s / 64MB
总通过数：27209
总尝试数：46898
来源：模板题
算法标签
代码：

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

const int N = 300010;

int n, m;
int a[N], s[N];//a数组存数, s数组存前缀和

vector<int> alls; //存原来的坐标x 
vector< pair<int, int> > add, query; //两种操作 

int find(int x)   //求x这个值离散化后的结果 
{
    int l=0, r=alls.size()-1;
    while(l < r)
    {
        int mid = l+r >> 1;
        if(alls[mid]>=x)
            r = mid;
        else
            l = mid+1;
    } 
    return r+1;
} 

int main()
{
    cin >> n >> m;
    for(int i=0; i<n; i++)
    {
        int x, c;
        cin >> x >> c;
        add.push_back({x, c}); 
        alls.push_back(x); 
    } 

    for(int i=0; i<m; i++)
    {
        int l, r;
        cin >> l >> r;
        query.push_back({l, r});

        alls.push_back(l);
        alls.push_back(r);  
    }

    //去重
    sort(alls.begin(), alls.end());
    alls.erase(unique(alls.begin(), alls.end() ), alls.end() );  //unique()返回去重后数组的最后一位下标,后面都是重复元素

    //处理插入离散化后的数组 
    for(auto item : add)
    {
        int x = find(item.first);
        a[x] += item.second;
    }

    //预处理前缀和
    for(int i=1; i<=alls.size(); i++)
        s[i] = s[i-1] + a[i];

    //处理询问
    for(auto item : query)
    {
        int l = find(item.first);
        int r = find(item.second);
        cout << s[r] - s[l-1] << endl;
    } 

    return 0;
}

（2）、K倍区间
给定一个长度为 N 的数列，A1,A2,…AN，如果其中一段连续的子序列 Ai,Ai+1,…Aj 之和是 K 的倍数，我们就称这个区间 [i,j] 是 K 倍区间。

你能求出数列中总共有多少个 K 倍区间吗？

输入格式
第一行包含两个整数 N 和 K。

以下 N 行每行包含一个整数 Ai。

输出格式
输出一个整数，代表 K 倍区间的数目。

数据范围
1≤N,K≤100000,
1≤Ai≤100000
输入样例：
5 2
1
2
3
4
5
输出样例：
6
难度：中等
时/空限制：1s / 64MB
总通过数：5612
总尝试数：14501
来源：第八届蓝桥杯省赛C++B组,第八届蓝桥杯省赛JAVAB组
算法标签

代码:

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

typedef long long LL;

const int N = 100010;

int n, k;
LL s[N], cnt[N];

int main()
{
    scanf("%d%d", &n, &k);
    for (int i = 1; i <= n; i ++ )
    {
        scanf("%lld", &s[i]);
        s[i] += s[i - 1];
    }

    LL res=0;
    cnt[0]=1;   //s[0]也有，余数为0
    for(int i=1;i<=n;i++)
    {
        res+=cnt[s[i]%k];
        cnt[s[i]%k]++;
    }


    printf("%lld\n", res);

    return 0;
}

二维前缀和 —— 模板题 AcWing 796. 子矩阵的和
S[i, j] = 第i行j列格子左上部分所有元素的和
以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵的和为：
S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]

（1）子矩阵的和
输入一个 n 行 m 列的整数矩阵，再输入 q 个询问，每个询问包含四个整数 x1,y1,x2,y2，表示一个子矩阵的左上角坐标和右下角坐标。

对于每个询问输出子矩阵中所有数的和。

输入格式
第一行包含三个整数 n，m，q。

接下来 n 行，每行包含 m 个整数，表示整数矩阵。

接下来 q 行，每行包含四个整数 x1,y1,x2,y2，表示一组询问。

输出格式
共 q 行，每行输出一个询问的结果。

数据范围
1≤n,m≤1000,
1≤q≤200000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤矩阵内元素的值≤1000
输入样例：
3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4
输出样例：
17
27
21

代码：

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>

const int N = 1010;
using namespace std;
int a[N][N];
int s[N][N];
int n,m,q;

int main()
{
    cin>>n>>m>>q;
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            scanf("%d",&a[i][j]);
        }
    }

    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            s[i][j]=s[i-1][j]+s[i][j-1]+a[i][j]-s[i-1][j-1];
        }
    }

    while(q--)
    {
        int x1,y1,x2,y2;
        cin>>x1>>y1>>x2>>y2;
        printf("%d\n",s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1]);
    }
    return 0;
}

一维差分：给区间[l, r]中的每个数加上c：B[l] += c, B[r + 1] -= c

(1)输入一个长度为 n 的整数序列。

接下来输入 m 个操作，每个操作包含三个整数 l,r,c，表示将序列中 [l,r] 之间的每个数加上 c。

请你输出进行完所有操作后的序列。

输入格式
第一行包含两个整数 n 和 m。

第二行包含 n 个整数，表示整数序列。

接下来 m 行，每行包含三个整数 l，r，c，表示一个操作。

输出格式
共一行，包含 n 个整数，表示最终序列。

数据范围
1≤n,m≤100000,
1≤l≤r≤n,
−1000≤c≤1000,
−1000≤整数序列中元素的值≤1000
输入样例：
6 3
1 2 2 1 2 1
1 3 1
3 5 1
1 6 1
输出样例：
3 4 5 3 4 2
代码

#include <iostream>

using namespace std;

const int N = 100010;

int n, m;
int a[N], b[N];

void insert(int l, int r, int c)
{
    b[l] += c;
    b[r + 1] -= c;
}

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);

    for (int i = 1; i <= n; i ++ ) insert(i, i, a[i]);

    while (m -- )
    {
        int l, r, c;
        scanf("%d%d%d", &l, &r, &c);
        insert(l, r, c);
    }

    for (int i = 1; i <= n; i ++ ) b[i] += b[i - 1];

    for (int i = 1; i <= n; i ++ ) printf("%d ", b[i]);

    return 0;
}

(2)、增减序列
给定一个长度为 n 的数列 a1,a2,…,an，每次可以选择一个区间 [l,r]，使下标在这个区间内的数都加一或者都减一。

求至少需要多少次操作才能使数列中的所有数都一样，并求出在保证最少次数的前提下，最终得到的数列可能有多少种。

输入格式
第一行输入正整数 n。

接下来 n 行，每行输入一个整数，第 i+1 行的整数代表 ai。

输出格式
第一行输出最少操作次数。

第二行输出最终能得到多少种结果。

数据范围
0<n≤105,
0≤ai<2147483648
输入样例：
4
1
1
2
2
输出样例：
1
2

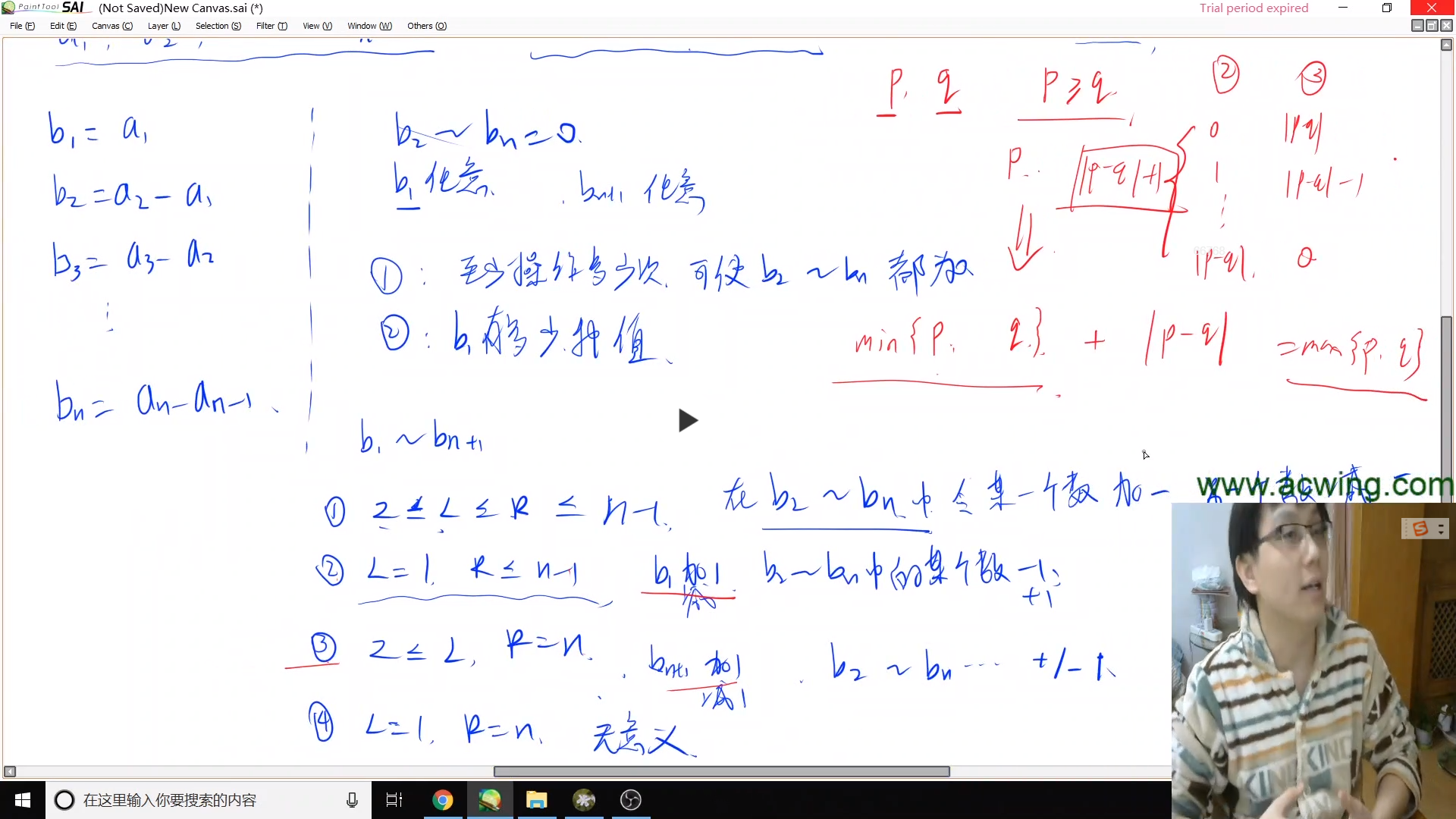
代码：

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 100010;

typedef long long LL;

int n;
int a[N], b[N];

int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
    for (int i = 1; i <= n; i ++ ) b[i] = a[i] - a[i - 1];

    LL p = 0, q = 0;
    for (int i = 2; i <= n; i ++ )
        if (b[i] > 0) p += b[i];
        else q -= b[i];

    cout << max(p, q) << endl;
    cout << abs(p - q) + 1 << endl;

    return 0;
}

二维差分
给以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵中的所有元素加上c：
S[x1, y1] += c, S[x2 + 1, y1] -= c, S[x1, y2 + 1] -= c, S[x2 + 1, y2 + 1] += c

（1）差分矩阵
输入一个 n 行 m 列的整数矩阵，再输入 q 个操作，每个操作包含五个整数 x1,y1,x2,y2,c，其中 (x1,y1) 和 (x2,y2) 表示一个子矩阵的左上角坐标和右下角坐标。

每个操作都要将选中的子矩阵中的每个元素的值加上 c。

请你将进行完所有操作后的矩阵输出。

输入格式
第一行包含整数 n,m,q。

接下来 n 行，每行包含 m 个整数，表示整数矩阵。

接下来 q 行，每行包含 5 个整数 x1,y1,x2,y2,c，表示一个操作。

输出格式
共 n 行，每行 m 个整数，表示所有操作进行完毕后的最终矩阵。

数据范围
1≤n,m≤1000,
1≤q≤100000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤c≤1000,
−1000≤矩阵内元素的值≤1000
输入样例：
3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
1 1 2 2 1
1 3 2 3 2
3 1 3 4 1
输出样例：
2 3 4 1
4 3 4 1
2 2 2 2

代码

#include <iostream>

using namespace std;

const int N = 1010;

int n, m, q;
int a[N][N], b[N][N];

void insert(int x1, int y1, int x2, int y2, int c)
{
    b[x1][y1] += c;
    b[x2 + 1][y1] -= c;
    b[x1][y2 + 1] -= c;
    b[x2 + 1][y2 + 1] += c;
}

int main()
{
    scanf("%d%d%d", &n, &m, &q);

    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            scanf("%d", &a[i][j]);

    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            insert(i, j, i, j, a[i][j]);

    while (q -- )
    {
        int x1, y1, x2, y2, c;
        cin >> x1 >> y1 >> x2 >> y2 >> c;
        insert(x1, y1, x2, y2, c);
    }

    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];

    for (int i = 1; i <= n; i ++ )
    {
        for (int j = 1; j <= m; j ++ ) printf("%d ", b[i][j]);
        puts("");
    }

    return 0;
}
https://www.acwing.com/solution/content/27325/

(2)激光炸弹
地图上有 N 个目标，用整数 Xi,Yi 表示目标在地图上的位置，每个目标都有一个价值 Wi。

注意：不同目标可能在同一位置。

现在有一种新型的激光炸弹，可以摧毁一个包含 R×R 个位置的正方形内的所有目标。

激光炸弹的投放是通过卫星定位的，但其有一个缺点，就是其爆炸范围，即那个正方形的边必须和 x，y 轴平行。

求一颗炸弹最多能炸掉地图上总价值为多少的目标。

输入格式
第一行输入正整数 N 和 R，分别代表地图上的目标数目和正方形的边长，数据用空格隔开。

接下来 N 行，每行输入一组数据，每组数据包括三个整数 Xi,Yi,Wi，分别代表目标的 x 坐标，y 坐标和价值，数据用空格隔开。

输出格式
输出一个正整数，代表一颗炸弹最多能炸掉地图上目标的总价值数目。

数据范围
0≤R≤109
0<N≤10000,
0≤Xi,Yi≤5000
0≤Wi≤1000
输入样例：
2 1
0 0 1
1 1 1
输出样例：
1
代码：

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 5010;

int s[N][N];

int main()
{
    int n, R;
    scanf("%d%d", &n, &R);
    R = min(R, 5001);

    for (int i = 0; i < n; i ++ )
    {
        int x, y, w;
        scanf("%d%d%d", &x, &y, &w);
        x ++, y ++ ;
        s[x][y] += w;
    }

    for (int i = 1; i <= 5001; i ++ )
        for (int j = 1; j <= 5001; j ++ )
            s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];

    int res = 0;
    for (int i = R; i <= 5001; i ++ )
        for (int j = R; j <= 5001; j ++ )
            res = max(res, s[i][j] - s[i - R][j] - s[i][j - R] + s[i - R][j - R]);

    printf("%d\n", res);

    return 0;
}

(3)、赶牛入圈
农夫约翰希望为他的奶牛们建立一个畜栏。

这些挑剔的畜生要求畜栏必须是正方形的，而且至少要包含 C 单位的三叶草，来当做它们的下午茶。

畜栏的边缘必须与 X，Y 轴平行。

约翰的土地里一共包含 N 单位的三叶草，每单位三叶草位于一个 1×1 的土地区域内，区域位置由其左下角坐标表示，并且区域左下角的 X,Y 坐标都为整数，范围在 1 到 10000 以内。

多个单位的三叶草可能会位于同一个 1×1 的区域内，因为这个原因，在接下来的输入中，同一个区域坐标可能出现多次。

只有一个区域完全位于修好的畜栏之中，才认为这个区域内的三叶草在畜栏之中。

请你帮约翰计算一下，能包含至少 C 单位面积三叶草的情况下，畜栏的最小边长是多少。

输入格式
第一行输入两个整数 C 和 N。

接下来 N 行，每行输入两个整数 X 和 Y，代表三叶草所在的区域的 X,Y 坐标。

同一行数据用空格隔开。

输出格式
输出一个整数，代表畜栏的最小边长。

数据范围
1≤C≤500,
C≤N≤500
输入样例：
3 4
1 2
2 1
4 1
5 2
输出样例：
4
难度：中等
时/空限制：1s / 64MB
总通过数：1528
总尝试数：4315
来源：《算法竞赛进阶指南》
算法标签

代码：

#include <cstring>
#include <iostream>
#include <algorithm>
#include <vector>

using namespace std;

typedef pair<int,int> PII;
const int N = 1010;

int n, m;
PII points[N];
int sum[N][N];
vector<int> numbers;

bool check(int len)
{
    for (int x1 = 1, x2 = 1; x2 < numbers.size(); x2 ++ )
    {
        while (numbers[x2] - numbers[x1 ] + 1 > len) x1 ++ ;
        for (int y1 =1, y2 = 1; y2 < numbers.size(); y2 ++ )
        {
            while (numbers[y2] - numbers[y1 ] + 1 > len) y1 ++ ;
            if (sum[x2][y2] - sum[x1-1][y2] - sum[x2][y1-1] + sum[x1-1][y1-1] >= m)
                return true;
        }
    }
    return false;
}

int get(int x)
{
    int l = 0, r = numbers.size() - 1;
    while (l < r)
    {
        int mid = l + r >> 1;
        if (numbers[mid] >= x) r = mid;
        else l = mid + 1;
    }
    return r;
}

// int get_id(int n)
// {
//     return lower_bound(numbers.begin(), numbers.end(), n) - numbers.begin();
// }


int main()
{
    cin >> m >> n;
    numbers.push_back(0);
    for (int i = 0; i < n; i ++ )
    {
        int x, y;
        cin >> x >> y;
        numbers.push_back(x);
        numbers.push_back(y);
        points[i] = {x, y};
    }
    sort(numbers.begin(), numbers.end());
    numbers.erase(unique(numbers.begin(), numbers.end()), numbers.end());

    for (int i = 0; i < n; i ++ )
    {
        int x = get(points[i].first), y = get(points[i].second);
        sum[x][y] ++ ;
    }

    for (int i = 1; i < numbers.size(); i ++ )
        for (int j = 1; j < numbers.size(); j ++ )
            sum[i][j] += sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1];

    int l = 1, r = 10000;
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;
        else l = mid + 1;
    }

    cout << r << endl;

    return 0;
}

总结：不同于之前的激光炸弹，激光炸弹因为不能算边界，所以不需要-1。