(1)大盗阿福
阿福是一名经验丰富的大盗。趁着月黑风高,阿福打算今晚洗劫一条街上的店铺。
这条街上一共有 N 家店铺,每家店中都有一些现金。
阿福事先调查得知,只有当他同时洗劫了两家相邻的店铺时,街上的报警系统才会启动,然后警察就会蜂拥而至。
作为一向谨慎作案的大盗,阿福不愿意冒着被警察追捕的风险行窃。
他想知道,在不惊动警察的情况下,他今晚最多可以得到多少现金?
输入格式
输入的第一行是一个整数 T,表示一共有 T 组数据。
接下来的每组数据,第一行是一个整数 N ,表示一共有 N 家店铺。
第二行是 N 个被空格分开的正整数,表示每一家店铺中的现金数量。
每家店铺中的现金数量均不超过1000。
输出格式
对于每组数据,输出一行。
该行包含一个整数,表示阿福在不惊动警察的情况下可以得到的现金数量。
数据范围
1≤T≤50,
1≤N≤105
输入样例:
2
3
1 8 2
4
10 7 6 14
输出样例:
8
24
样例解释
对于第一组样例,阿福选择第2家店铺行窃,获得的现金数量为8。
对于第二组样例,阿福选择第1和4家店铺行窃,获得的现金数量为10+14=24。
代码:
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
const int N = 1e5+10;
int f[N][2]; 二维0代表不偷,1代表偷
int a[N];
int T;
int n;
int main()
{
cin>>T;
while(T--)
{
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
memset(f,sizeof(f),0);
for(int i=1;i<=n;i++)
{
f[i][0]=max(f[i-1][1],f[i-1][0]);
f[i][1]=f[i-1][0]+a[i];
}
printf("%d\n", max(f[n][0], f[n][1]));
}
return 0;
}
(2)股票买卖(I)只可以买一次
给定一个长度为 N 的数组,数组中的第 i 个数字表示一个给定股票在第 i 天的价格。
如果你最多只允许完成一笔交易(即买入和卖出一支股票),设计一个算法来计算你所能获取的最大利润。
注意你不能在买入股票前卖出股票。
输入格式
第一行包含整数 N,表示数组长度。
第二行包含 N 个不大于 109 的正整数,表示完整的数组。
输出格式
输出一个整数,表示最大利润。
数据范围
1≤N≤105,
输入样例1:
6
7 1 5 3 6 4
输出样例1:
5
输入样例2:
5
7 6 4 3 1
输出样例2:
0
样例解释
样例1:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。注意利润不能是 7-1 = 6, 因为你不能在买入股票前卖出股票。
样例2:在这种情况下, 不进行任何交易, 所以最大利润为 0。
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
const int N = 1e5+10;
const int INF = 0x3f3f3f3f;
int w[N];
int f[N][2][2]; //0表示手中没货,1表示有货
int n,k;
int main()
{
cin>>n;
for(int i=1;i<=n;i++)cin>>w[i];
memset(f,-INF,sizeof(f));
for(int i=0;i<=n;i++) f[i][0][0]=0; //i要从0开始,第1天没货可以从第0天转移过来
for(int i=1;i<=n;i++)
{
f[i][1][0]=max(f[i-1][1][0],f[i-1][1][1]+w[i]); //上一次没买,这一次也没买,所以是j,不是j-1所以是f[i-1][j][0]
//而正在进行第j次交易卖出去,所示是f[i-1][j][1]+w[i]
f[i][1][1]=max(f[i-1][1][1],f[i-1][0][0]-w[i]);//上一次没卖,这一次也没卖,所以是j,不是j-1所以是f[i-1][j][1]
//正在进行第j次交易,在转移之前已经进行j-1次交易,所以是f[i-1][j-1][0]-w[i]
}
int res = 0;
for (int i = 0; i <= 1; i ++ ) res = max(res, f[n][i][0]);
printf("%d\n", res);
return 0;
}
(3)股票买票(II)尽可能买多次
给定一个长度为 N 的数组,数组中的第 i 个数字表示一个给定股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
输入格式
第一行包含整数 N,表示数组长度。
第二行包含 N 个不大于 10000 的正整数,表示完整的数组。
输出格式
输出一个整数,表示最大利润。
数据范围
1≤N≤105
输入样例1:
6
7 1 5 3 6 4
输出样例1:
7
输入样例2:
5
1 2 3 4 5
输出样例2:
4
输入样例3:
5
7 6 4 3 1
输出样例3:
0
样例解释
样例1:在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。共得利润 4+3 = 7。
样例2:在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
样例3:在这种情况下, 不进行任何交易, 所以最大利润为 0。
代码:
#include <iostream>
using namespace std;
const int N = 1e5 + 10, INF = 0x3f3f3f3f;
int n;
int w[N];
int f[N][2]; //0表示手中没货,1表示有货
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%d", &w[i]);
f[0][1] = -INF;
for (int i = 1; i <= n; ++i) {
f[i][0] = max(f[i - 1][0], f[i - 1][1] + w[i]);
f[i][1] = max(f[i - 1][1], f[i - 1][0] - w[i]);
}
printf("%d\n", f[n][0]);
return 0;
}
(4)股票买票(III)最多可交易2次
给定一个长度为 N 的数组,数组中的第 i 个数字表示一个给定股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成两笔交易。
注意: 你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
输入格式
第一行包含整数 N,表示数组长度。
第二行包含 N 个不大于 109 的正整数,表示完整的数组。
输出格式
输出一个整数,表示最大利润。
数据范围
1≤N≤105
输入样例1:
8
3 3 5 0 0 3 1 4
输出样例1:
6
输入样例2:
5
1 2 3 4 5
输出样例2:
4
输入样例3:
5
7 6 4 3 1
输出样例3:
0
样例解释
样例1:在第 4 天(股票价格 = 0)的时候买入,在第 6 天(股票价格 = 3)的时候卖出,这笔交易所能获得利润 = 3-0 = 3 。随后,在第 7 天(股票价格 = 1)的时候买入,在第 8 天 (股票价格 = 4)的时候卖出,这笔交易所能获得利润 = 4-1 = 3 。共得利润 3+3 = 6。
样例2:在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
样例3:在这种情况下, 不进行任何交易, 所以最大利润为 0。
代码:
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
const int N = 1e5+10;
const int INF = 0x3f3f3f3f;
int w[N];
int f[N][3][2]; //0表示手中没货,1表示有货
int n,k;
int main()
{
cin>>n;
for(int i=1;i<=n;i++)cin>>w[i];
memset(f,-INF,sizeof(f));
for(int i=0;i<=n;i++) f[i][0][0]=0; //i要从0开始,第1天没货可以从第0天转移过来
for(int i=1;i<=n;i++)
{
for(int j=1;j<=2;j++)
{
f[i][j][0]=max(f[i-1][j][0],f[i-1][j][1]+w[i]); //上一次没买,这一次也没买,所以是j,不是j-1所以是f[i-1][j][0]
//而正在进行第j次交易卖出去,所示是f[i-1][j][1]+w[i]
f[i][j][1]=max(f[i-1][j][1],f[i-1][j-1][0]-w[i]);//上一次没卖,这一次也没卖,所以是j,不是j-1所以是f[i-1][j][1]
//正在进行第j次交易,在转移之前已经进行j-1次交易,所以是f[i-1][j-1][0]-w[i]
}
}
int res = 0;
for (int i = 0; i <= 2; i ++ ) res = max(res, f[n][i][0]);
printf("%d\n", res);
return 0;
}
(5)股票买票(IV) 最多可交易k次
给定一个长度为 N 的数组,数组中的第 i 个数字表示一个给定股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润,你最多可以完成 k 笔交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。一次买入卖出合为一笔交易。
输入格式
第一行包含整数 N 和 k,表示数组的长度以及你可以完成的最大交易数量。
第二行包含 N 个不超过 10000 的正整数,表示完整的数组。
输出格式
输出一个整数,表示最大利润。
数据范围
1≤N≤105,
1≤k≤100
输入样例1:
3 2
2 4 1
输出样例1:
2
输入样例2:
6 2
3 2 6 5 0 3
输出样例2:
7
样例解释
样例1:在第 1 天 (股票价格 = 2) 的时候买入,在第 2 天 (股票价格 = 4) 的时候卖出,这笔交易所能获得利润 = 4-2 = 2 。
样例2:在第 2 天 (股票价格 = 2) 的时候买入,在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4 。随后,在第 5 天 (股票价格 = 0) 的时候买入,在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。共计利润 4+3 = 7.
代码:
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
const int K =105;
const int N = 1e5+10;
const int INF = 0x3f3f3f3f;
int w[N];
int f[N][K][2]; //0表示手中没货,1表示有货
int n,k;
int main()
{
cin>>n>>k;
for(int i=1;i<=n;i++)cin>>w[i];
memset(f,-INF,sizeof(f));
for(int i=0;i<=n;i++) f[i][0][0]=0; //i要从0开始,第1天没货可以从第0天转移过来
for(int i=1;i<=n;i++)
{
for(int j=1;j<=k;j++)
{
f[i][j][0]=max(f[i-1][j][0],f[i-1][j][1]+w[i]); //上一次没买,这一次也没买,所以是j,不是j-1所以是f[i-1][j][0]
//而正在进行第j次交易卖出去,所示是f[i-1][j][1]+w[i]
f[i][j][1]=max(f[i-1][j][1],f[i-1][j-1][0]-w[i]);//上一次没卖,这一次也没卖,所以是j,不是j-1所以是f[i-1][j][1]
//正在进行第j次交易,在转移之前已经进行j-1次交易,所以是f[i-1][j-1][0]-w[i]
}
}
int res = 0;
for (int i = 0; i <= k; i ++ ) res = max(res, f[n][i][0]);
printf("%d\n", res);
return 0;
}
(6)股票买票(V) 有冷冻期
给定一个长度为 N 的数组,数组中的第 i 个数字表示一个给定股票在第 i 天的价格。
设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
卖出股票后,你无法在第二天买入股票 (即冷冻期为 1 天)。
输入格式
第一行包含整数 N,表示数组长度。
第二行包含 N 个不超过 10000 的正整数,表示完整的数组。
输出格式
输出一个整数,表示最大利润。
数据范围
1≤N≤105
输入样例:
5
1 2 3 0 2
输出样例:
3
样例解释
对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出],第一笔交易可得利润 2-1 = 1,第二笔交易可得利润 2-0 = 2,共得利润 1+2 = 3。
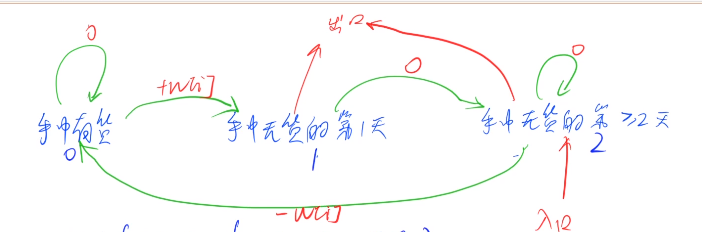
代码:
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1e5+10;
int w[N];
int f[N][3];
int n;
const int INF = 0x3f3f3f;
int main()
{
cin>>n;
for(int i=1;i<=n;i++)scanf("%d",&w[i]);
f[0][0]=-INF;
f[0][1]=-INF;
f[0][2]=0;
for(int i=1;i<=n;i++)
{
f[i][0]=max(f[i-1][0],f[i-1][2]-w[i]);
f[i][1]=max(f[i-1][1],f[i-1][0]+w[i]);
f[i][2]=max(f[i - 1][2], f[i - 1][1]);
}
printf("%d\n", max(f[n][1], f[n][2]));
return 0;
}
(7)股票买票(VI)
给定一个长度为 N 的数组,数组中的第 i 个数字表示一个给定股票在第 i 天的价格,再给定一个非负整数 f,表示交易股票的手续费用。
设计一个算法来计算你所能获取的最大利润。
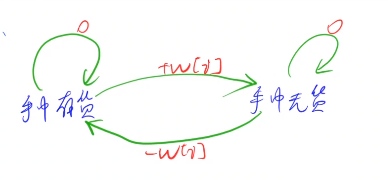
你可以无限次地完成交易,但是你每次交易都需要支付手续费。
注意: 你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
输入格式
第一行包含两个整数 N 和 f,分别表示数组的长度以及每笔交易的手续费用。
第二行包含 N 个不超过 10000 的正整数,表示完整的数组。
输出格式
输出一个整数,表示最大利润。
数据范围
1≤N≤105,
1≤f≤10000
输入样例:
6 2
1 3 2 8 4 9
输出样例:
8
样例解释
在第 1 天(股票价格 = 1)的时候买入,在第 4 天(股票价格 = 8)的时候卖出,这笔交易所能获得利润 = 8-1-2 = 5 。随后,在第 5 天(股票价格 = 4)的时候买入,在第 6 天 (股票价格 = 9)的时候卖出,这笔交易所能获得利润 = 9-4-2 = 3 。共得利润 5+3 = 8。
代码:
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10, INF = 0x3f3f3f3f;
int n;
int f1;
int w[N];
int f[N][2]; //0表示手中没货,1表示有货
int main() {
scanf("%d%d", &n,&f1);
for (int i = 1; i <= n; ++i) scanf("%d", &w[i]);
f[0][1] = -INF;
for (int i = 1; i <= n; ++i) {
f[i][0] = max(f[i - 1][0], f[i - 1][1] + w[i]-f1);
f[i][1] = max(f[i - 1][1], f[i - 1][0] - w[i]);
}
printf("%d\n", f[n][0]);
return 0;
}
总结:与(II)同,减去手续费即可

