试除法判定质数
给定 n 个正整数 ai,判定每个数是否是质数。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含一个正整数 ai。
输出格式
共 n 行,其中第 i 行输出第 i 个正整数 ai 是否为质数,是则输出 Yes,否则输出 No。
数据范围
1≤n≤100,
1≤ai≤231−1
输入样例:
2
2
6
输出样例:
Yes
No
代码:
#include<stdio.h>
#include<iostream>
using namespace std;
bool is_prime(int x)
{
if(x<2) return false;
for(int i=2;i<=x/i;i++)
{
if(x%i==0)return false;
}
return true;
}
int main()
{
int n;
int l;
scanf("%d",&n);
while(n--)
{
scanf("%d",&l);
if(is_prime(l))
{
printf("Yes\n");
}
else
{
printf("No\n");
}
}
}
总结:一个数的因数都是成对出现的:例如12的因数有3和4,2和6
所以我们可以只枚举较小的那一个,即根下n,假设较小的为d,较大的为n/d;
1.最普通的筛法 O(nlogn)O(nlogn)
C++ 代码
void get_primes2(){
for(int i=2;i<=n;i++){
if(!st[i]) primes[cnt++]=i;//把素数存起来
for(int j=i;j<=n;j+=i){//不管是合数还是质数,都用来筛掉后面它的倍数
st[j]=true;
}
}
}
2.诶氏筛法 O(nloglogn)O(nloglogn)
C++ 代码
void get_primes1(){
for(int i=2;i<=n;i++){
if(!st[i]){
primes[cnt++]=i;
for(int j=i;j<=n;j+=i) st[j]=true;//可以用质数就把所有的合数都筛掉;
}
}
}
3.线性筛法 O(n)O(n)
C++ 代码
void get_primes(){
//外层从2~n迭代,因为这毕竟算的是1~n中质数的个数,而不是某个数是不是质数的判定
for(int i=2;i<=n;i++){
if(!st[i]) primes[cnt++]=i;
for(int j=0;primes[j]<=n/i;j++){//primes[j]<=n/i:变形一下得到——primes[j]*i<=n,把大于n的合数都筛了就
//没啥意义了
st[primes[j]*i]=true;//用最小质因子去筛合数
//1)当i%primes[j]!=0时,说明此时遍历到的primes[j]不是i的质因子,那么只可能是此时的primes[j]<i的
//最小质因子,所以primes[j]*i的最小质因子就是primes[j];
//2)当有i%primes[j]==0时,说明i的最小质因子是primes[j],因此primes[j]*i的最小质因子也就应该是
//prime[j],之后接着用st[primes[j+1]*i]=true去筛合数时,就不是用最小质因子去更新了,因为i有最小
//质因子primes[j]<primes[j+1],此时的primes[j+1]不是primes[j+1]*i的最小质因子,此时就应该
//退出循环,避免之后重复进行筛选。
if(i%primes[j]==0) break;
}
}
作者:orzorz
链接:https://www.acwing.com/solution/content/7950/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
(2)哥德马赫猜想
哥德巴赫猜想的内容如下:
任意一个大于 4 的偶数都可以拆成两个奇素数之和。
例如:
8=3+5
20=3+17=7+13
42=5+37=11+31=13+29=19+23
现在,你的任务是验证所有小于一百万的偶数能否满足哥德巴赫猜想。
输入格式
输入包含多组数据。
每组数据占一行,包含一个偶数 n。
读入以 0 结束。
输出格式
对于每组数据,输出形如 n = a + b,其中 a,b 是奇素数。
若有多组满足条件的 a,b,输出 b−a 最大的一组。
若无解,输出 Goldbach’s conjecture is wrong.。
数据范围
6≤n<106
输入样例:
8
20
42
0
输出样例:
8 = 3 + 5
20 = 3 + 17
42 = 5 + 37
难度:简单
时/空限制:1s / 64MB
总通过数:2439
总尝试数:4177
来源:《信息学奥赛一本通》
算法标签

代码:
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
int n;
const int N = 1000010;
int primes[N];
bool st[N];
int cnt;
void init(int n)
{
for(int i=2;i<=n;i++)
{
if(!st[i])primes[cnt++]=i;
for(int j=0;primes[j]<=n/i;j++)
{
st[primes[j]*i]=true;
if(i%primes[j]==0)break;
}
}
}
int main()
{
init(N-1);
while(cin>>n,n)
{
for(int i=1;;i++)
{
int a=primes[i];
int b=n-a;
if(!st[b])
{
printf("%d = %d + %d\n",n,a,b);
break;
}
}
}
return 0;
}
(3)夏洛克和他的女朋友
夏洛克有了一个新女友(这太不像他了!)。
情人节到了,他想送给女友一些珠宝当做礼物。
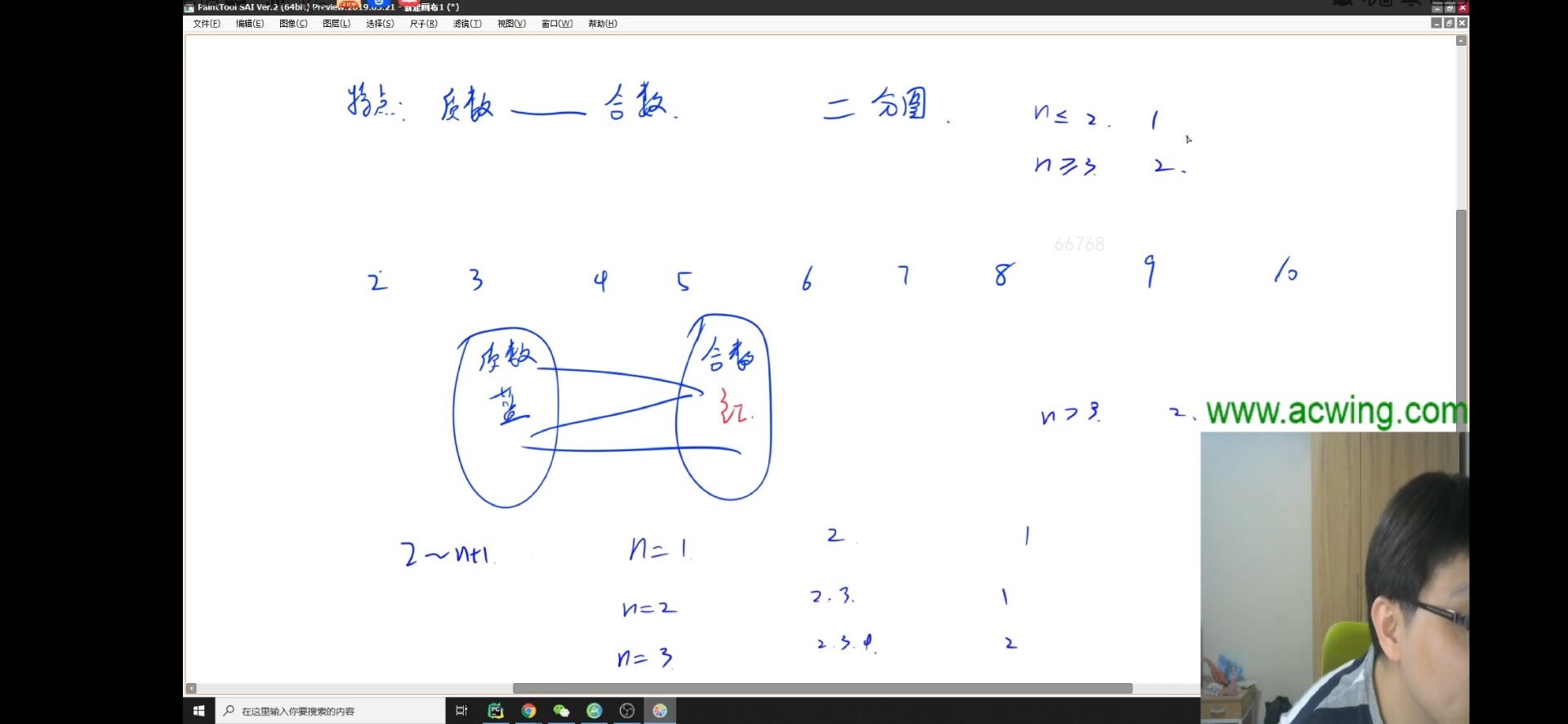
他买了 n 件珠宝,第 i 件的价值是 i+1,也就是说,珠宝的价值分别为 2,3,…,n+1。
华生挑战夏洛克,让他给这些珠宝染色,使得一件珠宝的价格是另一件珠宝的价格的质因子时,两件珠宝的颜色不同。
并且,华生要求他使用的颜色数尽可能少。
请帮助夏洛克完成这个简单的任务。
输入格式
只有一行一个整数 n,表示珠宝件数。
输出格式
第一行一个整数 k,表示所使用的颜色数;
第二行 n 个整数,表示第 1 到第 n 件珠宝被染成的颜色。
若有多种答案,输出任意一种。
请用 1 到 k 表示你用到的颜色。
数据范围
1≤n≤105
输入样例1:
3
输出样例1:
2
1 1 2
输入样例2:
4
输出样例2:
2
2 1 1 2
代码
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
const int N = 1e5+10;
int cnt;
int primes[N];
bool st[N];
void init(int n)
{
for(int i=2;i<=n;i++)
{
if(!st[i])primes[cnt++]=i;
for(int j=0;primes[j]<=n/i;j++)
{
st[primes[j]*i]=true;
if(i%primes[j]==0)break;
}
}
}
int n;
int main()
{
init(N+1);
cin>>n;
if (n <= 2) puts("1");
else puts("2");
for (int i = 2; i <= n + 1; i ++ )
if (!st[i]) printf("1 ");
else printf("2 ");
return 0;
}
(4)质数距离
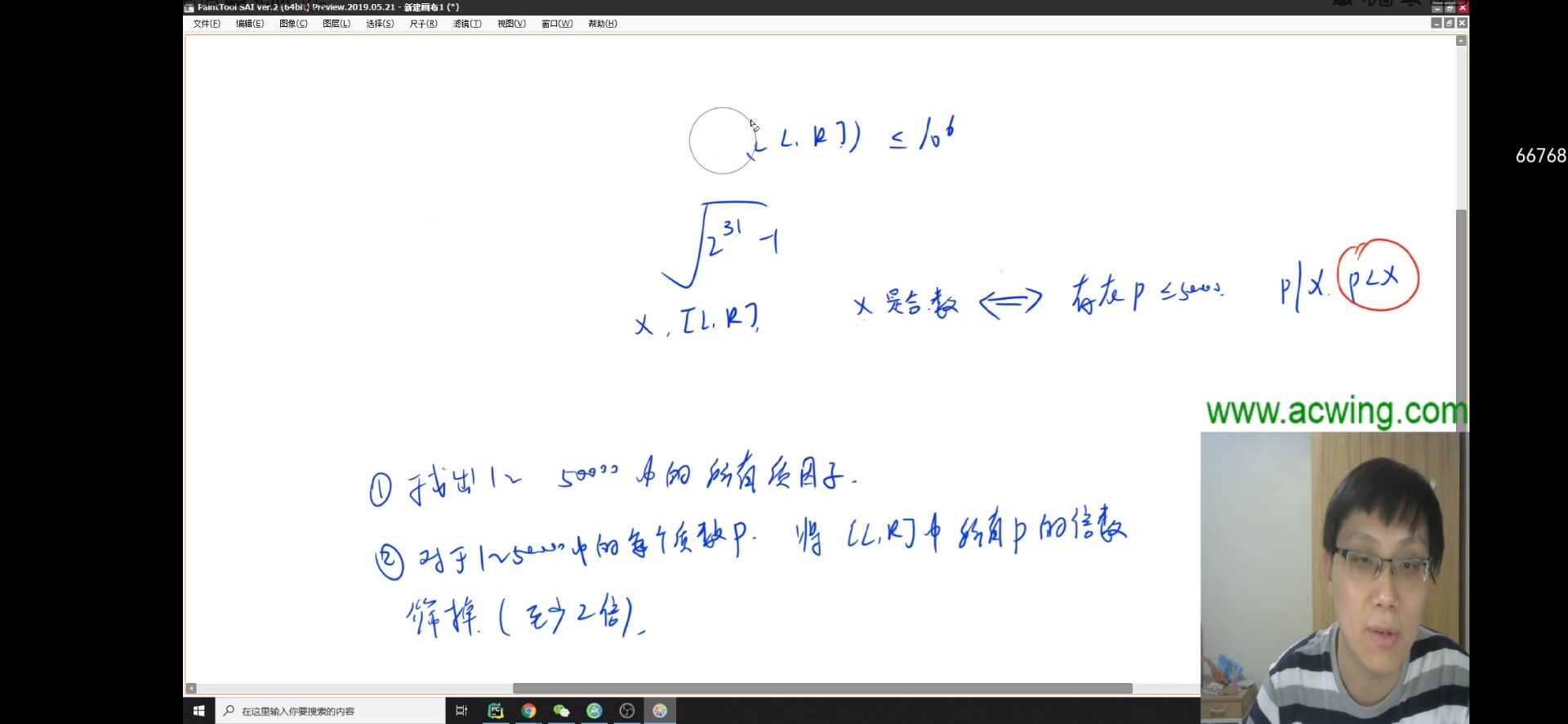
给定两个整数 L 和 U,你需要在闭区间 [L,U] 内找到距离最接近的两个相邻质数 C1 和 C2(即 C2−C1 是最小的),如果存在相同距离的其他相邻质数对,则输出第一对。
同时,你还需要找到距离最远的两个相邻质数 D1 和 D2(即 D1−D2 是最大的),如果存在相同距离的其他相邻质数对,则输出第一对。
输入格式
每行输入两个整数 L 和 U,其中 L 和 U 的差值不会超过 106。
输出格式
对于每个 L 和 U,输出一个结果,结果占一行。
结果包括距离最近的相邻质数对和距离最远的相邻质数对。(具体格式参照样例)
如果 L 和 U 之间不存在质数对,则输出 There are no adjacent primes.。
数据范围
1≤L<U≤231−1
输入样例:
2 17
14 17
输出样例:
2,3 are closest, 7,11 are most distant.
There are no adjacent primes.


代码:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long LL;
const int N = 1000010;
int primes[N], cnt;
bool st[N];
void init(int n)
{
memset(st, 0, sizeof st);
cnt = 0;
for (int i = 2; i <= n; i ++ )
{
if (!st[i]) primes[cnt ++ ] = i;
for (int j = 0; primes[j] * i <= n; j ++ )
{
st[i * primes[j]] = true;
if (i % primes[j] == 0) break;
}
}
}
int main()
{
int l, r;
while (cin >> l >> r)
{
init(50000);
memset(st, 0, sizeof st);
for (int i = 0; i < cnt; i ++ )
{
LL p = primes[i];//(1)LL p = primes[i],这里p用LL是因为如果p也是用int类型,本身l也是用int类型
//,如果l取得足够大,
//下面的l + p - 1会有可能直接爆int变成负数
for (LL j = max(p * 2, (l + p - 1) / p * p); j <= r; j += p)
//(2)这里的 j 是小于等于 r 的,而 r 的取值范围是小于2 ^ 31,这里确实是这样,可是这个循环跳出的
//条件是j <= r
//,也就是说如果r是最大的int,那么当j += p,
//要超过最大的int的时候需要比它还大才能跳出循环,
//因此直接爆int变成负数,然后j <= r依然成立,会一直死循环下去
//(3)因为(l + p - 1)/p可能等于p,然后错误地标记st[i] = true,
//这样就把一个质数p错误地标记成了合数,所以至少要从2*p开始
st[j - l] = true;
}
cnt=0;
for(int i=0;i<=r-l;i++)
{
if(!st[i]&&i+l>=2) //因为1不是质数也不是合数
{
primes[cnt ++ ] = i + l;
}
}
if (cnt < 2) puts("There are no adjacent primes.");
else
{
int minp = 0, maxp = 0;
for (int i = 0; i + 1 < cnt; i ++ )
{
int d = primes[i + 1] - primes[i];
if (d < primes[minp + 1] - primes[minp]) minp = i;
if (d > primes[maxp + 1] - primes[maxp]) maxp = i;
}
printf("%d,%d are closest, %d,%d are most distant.\n",
primes[minp], primes[minp + 1],
primes[maxp], primes[maxp + 1]);
}
}
return 0;
}
分解质因数
给定 n 个正整数 ai,将每个数分解质因数,并按照质因数从小到大的顺序输出每个质因数的底数和指数。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含一个正整数 ai。
输出格式
对于每个正整数 ai,按照从小到大的顺序输出其分解质因数后,每个质因数的底数和指数,每个底数和指数占一行。
每个正整数的质因数全部输出完毕后,输出一个空行。
数据范围
1≤n≤100,
2≤ai≤2×109
输入样例:
2
6
8
输出样例:
2 1
3 1
2 3
代码:
#include<iostream>
using namespace std;
void FenJie(int n)
{
for(int i=2;i<=n/i;i++)
{
int res=0;
if(n%i==0)
{
while(n%i==0)
{
n=n/i;res++;
}
cout << i << ' ' <<res << endl;
}
}
if(n>1)
{
cout<<n<<" "<<1<<endl;
}
cout<<endl;
}
int main()
{
int n;
int k;
scanf("%d",&n);
while(n--)
{
scanf("%d",&k);
FenJie(k);
}
return 0;
}
阶乘分解
给定整数 N,试把阶乘 N! 分解质因数,按照算术基本定理的形式输出分解结果中的 pi 和 ci 即可。
输入格式
一个整数 N。
输出格式
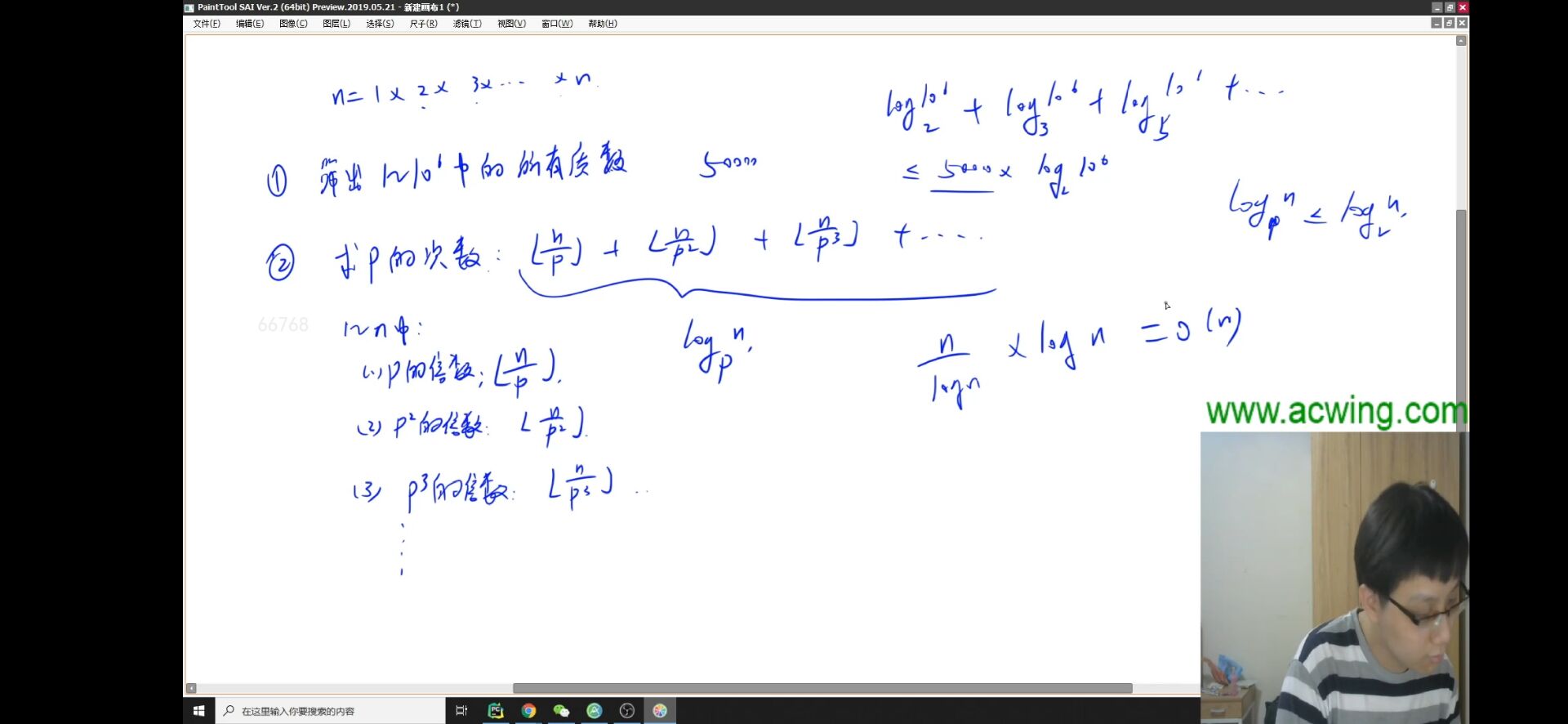
N! 分解质因数后的结果,共若干行,每行一对 pi,ci,表示含有 pcii 项。按照 pi 从小到大的顺序输出。
数据范围
3≤N≤106
输入样例:
5
输出样例:
2 3
3 1
5 1
样例解释
5!=120=23∗3∗5
代码:
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
const int N = 1e6+10;
bool st[N];
int cnt;
int primes[N];
int n;
void init(int n)
{
for(int i=2;i<=n;i++)
{
if(!st[i])primes[cnt++]=i;
for(int j=0;primes[j]<=n/i;j++)
{
st[primes[j]*i]=true;
if(i%primes[j]==0)break;
}
}
}
int main()
{
cin>>n;
init(n);
for(int i=0;i<cnt;i++)
{
int p=primes[i];
int s=0;
for(int j=n;j;j/=p)s+=j/p;
printf("%d %d\n",p,s);
}
return 0;
}
(回文质数)
151 既是一个质数,又是一个回文数,因此它可以被称为回文质数。
现在给定两个整数 a,b ,请你找出在 [a,b] 范围内的所有回文质数。
输入格式
共一行,包含两个整数 a,b。
输出格式
按照从小到大的顺序输出所求范围内的所有回文质数。
每个数占一行。
数据范围
5≤a<b≤108
输入样例:
5 500
输出样例:
5
7
11
101
131
151
181
191
313
353
373
383
代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
using namespace std;
const int N = 1e8+10;
int cnt;
bool st[N];
int primes[N];
int a;
int b;
bool pd_h(int x)
{
int y = x, num = 0;
while (y != 0)
{
num = num * 10 + y % 10;
y /= 10;
}
if (num == x)
return true;
else
return false;
}
void init(int b)
{
for(int i=2;i<=b;i++)
{
if(!st[i])primes[cnt++]=i;
for(int j=0;primes[j]<=b/i;j++)
{
st[primes[j]*i]=true;
if(i%primes[j]==0)break;
}
}
}
int main()
{
cin>>a>>b;
if (b > 10000000)//这里是10^7 不是10^8,那题目给的是10^8为什么10^7可以过呢 不然会超时少这一句话
//这里涉及到一个知识,任何偶数位数的回文数都不是素数(11除外),原因可以百度。
//其实就是偶数位数的回文数可以被11整除,所以不会是素数
b = 10000000;
init(b);
for(int i=a;i<=b;i++)
{
if(pd_h(i)&&!st[i])
{
printf("%d\n",i);
}
}
return 0;
}
质因子
给定一个整数 N,找出它的所有质因子,并按如下格式输出:
N=pk11×pk22×…×pkmm
注意: 如果 N=1 则输出 1=1。
输入格式
一个整数 N。
输出格式
输出时,按 N=p1^k1p2^k2…*pm^km 的格式输出答案。
其中 pi 是质因子,应按照递增顺序排列,ki 是 pi 的指数,如果 ki 为 1,则不必输出。
数据范围
1≤N≤231−1
输入样例:
97532468
输出样例:
97532468=2^211171011291
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
int main ()
{
LL x;
scanf("%lld",&x);
printf("%lld=",x);
if(x==1)
{
cout<<"1";
return 0;
}
int t=0;
for(int i=2;i<=x / i;i++)
{
int co=0;
while(x%i==0)
{
x /= i;
co++;
}
if(co>0)
{
if(t==0)
{
t=1;
printf("%d",i);
}
else{
printf("*%d",i);
}
if(co>1) printf("^%d",co);
}
}
if(x>1)
{
if(t==1) printf("*%lld",x);
else printf("%lld",x);
}
return 0;
}
x的因子链
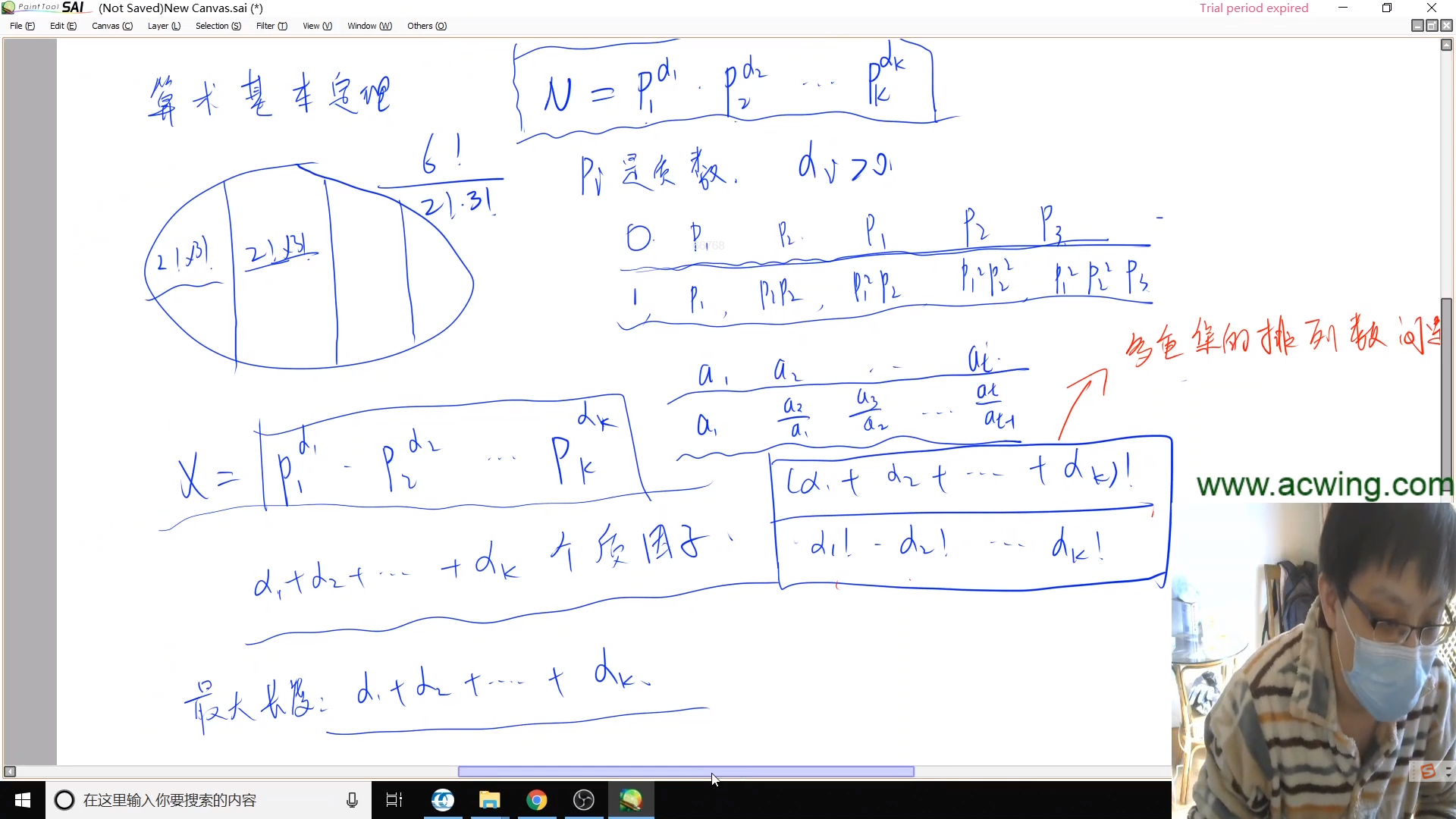
输入正整数 X,求 X 的大于 1 的因子组成的满足任意前一项都能整除后一项的严格递增序列的最大长度,以及满足最大长度的序列的个数。
输入格式
输入包含多组数据,每组数据占一行,包含一个正整数表示 X。
输出格式
对于每组数据,输出序列的最大长度以及满足最大长度的序列的个数。
每个结果占一行。
数据范围
1≤X≤220
输入样例:
2
3
4
10
100
输出样例:
1 1
1 1
2 1
2 2
4 6

代码:
// 2的20次方不会爆long long
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
typedef long long LL;
const int N = (1<<20)+10;
int primes[N];
int cnt;
bool st[N];
int minp[N]; //最小质因子
void init(int n)
{
for(int i=2;i<=n;i++)
{
if (!st[i])
{
minp[i] = i;
primes[cnt ++ ] = i;
}
for(int j=0;primes[j]*i<=n;j++)
{
st[i*primes[j]]=true;
minp[i*primes[j]]=primes[j];
if(i%primes[j]==0)
{
break;
}
}
}
}
int main()
{
init(N-1);
int fact[30], sum[N];
int x;
while (scanf("%d", &x) != -1)
{
int k = 0, tot = 0;
while (x > 1)
{
int p = minp[x];
fact[k] = p, sum[k] = 0;
while (x % p == 0)
{
x /= p;
sum[k] ++ ;
tot ++ ;
}
k ++ ;
}
LL res = 1;
for (int i = 1; i <= tot; i ++ ) res *= i;
for (int i = 0; i < k; i ++ )
for (int j = 1; j <= sum[i]; j ++ )
res /= j;
printf("%d %lld\n", tot, res);
}
return 0;
}
优质牛肋骨
农夫约翰的牛总是能够产出最优质的肋骨。
你可以通过查看约翰和美国农业部一对一地刻在每根肋骨上的数字来分辨它们。
约翰可以保证购买他的牛肋骨的消费者们一定可以得到最优质的肋骨。
因为每当从肋骨的右侧切下一部分卖给消费者时,剩下的相连的肋骨上的数字始终都能保持是一个质数。(单词 prime 作形容词可以表示优质的,作名词可以表示质数,这里一语双关)
例如,有四根肋骨连在一起,构成质数 7331,当卖掉最右边一根时,剩下的三个肋骨构成质数 733,再卖掉一根,剩下两根肋骨构成质数 73,再卖掉一根,最后剩下一根肋骨构成质数 7。
像 7331 这样的数字我们可以称之为长度为 4 的超级质数。
现在给定一个整数 N,请你求出长度为 N 的超级质数有哪些。
数字 1 不是质数。
输入格式
共一行,包含一个整数 N。
输出格式
按照从小到大的顺序输出所有长度为 N 的超级质数。
每个数占一行。
数据范围
1≤N≤8
输入样例:
4
输出样例:
2333
2339
2393
2399
2939
3119
3137
3733
3739
3793
3797
5939
7193
7331
7333
7393
代码:
#include<bits/stdc++.h>
using namespace std;
int a[4]={2,3,5,7},b[4]={1,3,7,9}; //a[]存最高位,b[]存其他位
bool primes(int x) //判别素数
{
for(int i=2;i<=x/i;i++)
{
if(x%i==0) return false;
}
return true;
}
int main()
{
int n; cin>>n;
//if(n==1) for(auto x:a) cout<<x<<endl;
queue<int> q; //队列把所有素数的首位数字即a[]所有元素存进来
for(auto x:a) q.push(x);
int l=pow(10,n-1),r=pow(10,n); //对答案范围进行规定
while(q.size())
{
auto t=q.front();
q.pop();
if(t>=l && t<r) cout<<t<<endl; //满足条件作为答案输出
for(int i=0;i<4;i++)
{
int temp=t*10+b[i];
if(temp<r)
if(primes(temp))
{
q.push(temp);
}
}
}
return 0;
}
总结:通过观察,当只有一位时,2,3,5,7为素数,当位数大于2时,只有1,3,7,9作为除了首位的其他位的数才能构成素数,
所以设一个a数组和一个b数组,
通过bfs()对所有由a数组元素开头,b数组元素垫后的数是否为素数,当这个数等于n位同时小于n+1位时可以作为一个答案进行输出。

