二分

整数二分算法模板

二分并不一定要求单调性，而是如下图所示，左边满足某个性质，右边也满足某个性质，然后可以根据二分求边界点。

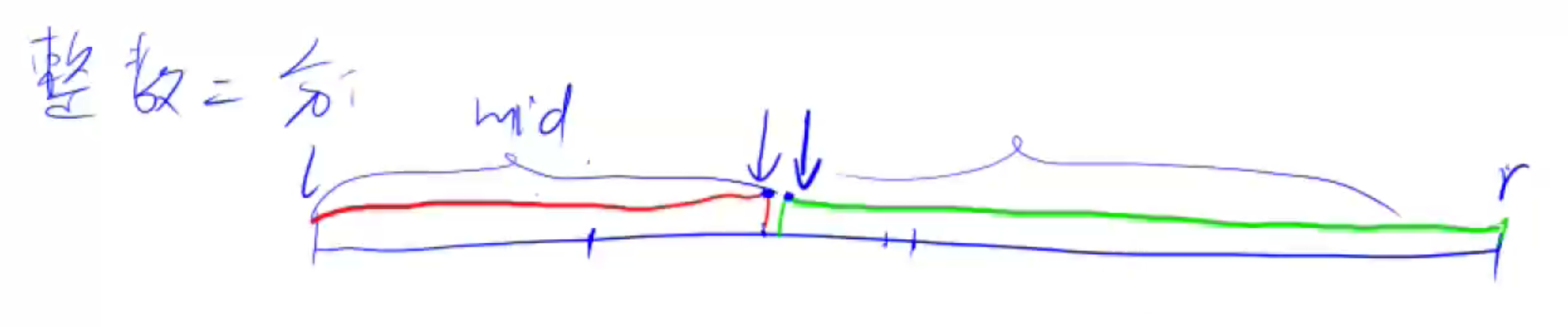
二分思路如下：先暂时令mid = (l + r) / 2，如果check(mid) == true，那么说明mid满足某个性质。如果是左边那个性质，说明解在mid右边，因此左边的l更新为mid，如果不满足则r = mid - 1；如果是右边那个性质，说明解在mid左边，因此右边的r更新为mid，如果不满足则l = mid + 1；二分的时候最好画一下图，然后更新区间。

注意：如果check(mid) == true时更新的左边，需要回过头来更新mid = (l + r + 1) / 2，如下面两个模板。

bool check(int x) {/* ... */} // 检查x是否满足某种性质

// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用：
int bsearch_1(int l, int r)
{
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;    // check()判断mid是否满足性质
        else l = mid + 1;
    }
    return l;
}
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用：
int bsearch_2(int l, int r)
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

例题

数的范围

给定一个按照升序排列的长度为 $n$ 的整数数组，以及 $q$ 个查询。

对于每个查询，返回一个元素 $k$ 的起始位置和终止位置（位置从 $0$ 开始计数）。

如果数组中不存在该元素，则返回 -1 -1。

思路： 先查找范围的左端点，设置需要检查的性质为左端点以右的满足a[i] >= k，为啥不取左端点以左的性质呢？因为左端点以左的性质为a[i] < k，该性质左端点并不满足，所以搜到的不是左端点，而是左端点左边的一个点，因此搜索完之后还需要进一步处理；同理，再查找范围的右端点，设置需要检查的性质为右端点以右的满足a[i] <= k

#include <iostream>
using namespace std;

const int N = 100010;

int a[N];
// 查找范围的右端点，右端点以右的满足a[i] >= k
int b_search1(int l, int r, int k) {
    while (l < r) {
        int mid = (l + r) >> 1;
        if (a[mid] >= k) r = mid;
        else l = mid + 1;
    }

    if (a[l] != k) return -1;
    return l;
}

// 查找范围的右端点，因为右端点以左的满足a[i] <= k
int b_search2(int l, int r, int k) {
    while (l < r) {
        int mid = (l + r + 1) >> 1;
        if (a[mid] <= k) l = mid;
        else r = mid - 1;
    }
    if(a[l] != k) return -1;
    return l;
}

int main () {
    int n, q;
    cin >> n >> q;
    for (int i = 0; i < n; i ++ ) cin >> a[i];

    for (int i = 0; i < q; i ++ ) {
        int k;
        cin >> k;
        int l = b_search1(0, n - 1, k);
        int r = b_search2(0, n - 1, k);
        cout << l << " " << r << endl;
    }
}

寻找峰值

峰值元素是指其值严格大于左右相邻值的元素。

给你一个整数数组 nums，找到峰值元素并返回其索引。数组可能包含多个峰值，在这种情况下，返回 任何一个峰值 所在位置即可。

你可以假设 nums[-1] = nums[n] = -∞。

你必须实现时间复杂度为 O(log n)的算法来解决此问题。

示例 1：

输入：nums = [1,2,3,1]
输出：2
解释：3 是峰值元素，你的函数应该返回其索引 2。

示例 2：

输入：nums = [1,2,1,3,5,6,4]
输出：1 或 5 
解释：你的函数可以返回索引 1，其峰值元素为 2；
     或者返回索引 5， 其峰值元素为 6。

思路：

题目中关键信息是 nums[-1] = nums[n] = -∞，这意味着不管 nums是升序还是降序都会有解，如果不是有序的也会有解，因此对于所有的 nums都会有解。这样我们就可以每次往相邻两个值较大的值走，比如如果 nums[mid] > nums[mid + 1]，则往左边走，选择区间[l, mid]，更新 r = mid，如果 nums[mid] < nums[mid + 1]，则往右边走，选择区间 [mid + 1, r]。

class Solution {
public:
    int findPeakElement(vector<int>& nums) {
        int n = nums.size();
        int l = 0, r = n - 1;
        while (l < r) {
            int mid = (l + r) >> 1;
            if (nums[mid] > nums[mid + 1]) r = mid;
            else l = mid + 1;
        }
        return l;
    }
};