题目来源：蓝桥杯模拟赛

算法1:暴力 50%
时间复杂度 $ O(2^n) $

1. 第二项从1~n枚举，因为是从第三项开始每个数字才是小于前面两个数字的绝对值之差
2. 利用一个全局变量记录方案数，每次只要dfs函数执行依次，方案数加1，dfs函数的作用是求出某个数字的前2个数字
   分别是last，cur的情况下的方案数

#include <iostream>
#include <cstring>
#include <algorithm>


using namespace std ;

const int mod = 10000 ;
int n ;
int ans ;

void dfs(int last,int cur){
    ans = (ans + 1) % mod ;
    for(int i=1;i<abs(last-cur);i++){
        dfs(cur,i) ;
    }
}

int main(){
    scanf("%d",&n) ;

    for(int i=1;i<=n;i++){
        dfs(n,i) ;
    }
    printf("%d\n",ans) ;

    return 0 ;
}

算法2：记忆化搜索80%

分析：从算法1可以看到由于每次递归都会重复计算相同的值，导致时间复杂度爆炸。因为当某个数字数列的前面两个数字确定的情况下数字序列的方案数是一样的，因此该问题是个无后效性问题，所以可以对算法1进行改进，用一个数组记录每次求得的结果,因为这题的状态定义比较特殊，所以采用记忆化搜索的方式来实现

时间复杂度：$ O(n^3) $
状态表示是两维的，状态转移是1维的，因此时间复杂度是 $ O(n^3) $

#include <bits/stdc++.h>

using namespace std;

const int N = 1010;
const int mod = 10000;

int f[N][N];

int dp(int last,int cur)
{
    if(f[last][cur] != -1) return f[last][cur];

    f[last][cur] = 1;

    for(int i = 1;i < abs(cur - last);i++)
         f[last][cur] = (f[last][cur] + dp(cur,i)) % mod;

    return f[last][cur];
}

int main(){


    memset(f,-1,sizeof f);

    int n;

    cin >> n;

    int res = 0;

    for(int i=1;i<=n;i++) res = (res + dp(n,i)) % mod;

    cout << res << endl;

    return 0;
}

算法3 改进版记忆化搜索 100%
时间复杂度 $O(n^2)$

优化思路：因为算法2我们在每次在计算 f[i][j]的时候都是循环枚举计算的导致复杂度爆炸
因此我们要对这部分下手，对状态转移进行优化，我们再来看看 f[i][j]表示的是什么，表示的
是前面两个数字分别是i,j的情况下的序列数，因此我们采用额外的数组g记录这个前缀和
g[i][j] = f[i][1]+f[i][2]+f[i][3]+...f[i][j],具体实现看代码

#include <iostream>
#include <cstring>
#include <cstdlib>
#include <cstdio>

using namespace std;

const int N = 1010;
const int mod = 10000;

int n;
int f[N][N], g[N][N];

int dp1(int last, int cur);
int dp2(int last, int cur);

//因为无后效性，所以一定不会出现死递归
int dp2(int last, int cur) {
    if (cur <= 0) return 0;

    if (g[last][cur] != -1)
        return g[last][cur];

    return g[last][cur] = (dp2(last, cur - 1) + dp1(last, cur)) % mod;
}


int dp1(int last, int cur) {//预处理前缀信息
    if (cur <= 0) return 0;

    if(f[last][cur] != -1)
        return f[last][cur];

    return f[last][cur] = (1 + dp2(cur, abs(last - cur) - 1)) % mod;
}

int main(){
    scanf("%d", &n);
    memset(f, -1, sizeof(f));
    memset(g, -1, sizeof(g));

    printf("%d\n", dp2(n, n));
    return 0;
}

算法4：究极版记忆化搜索
时间复杂度 $O(n^2)$

从算法3的分析我们看到 g[i][j] = f[i][1] + f[i][2] + f[i][3] + ... + f[i][j],那么我们为什么不直接用 f[i][j]存前缀和，那么现在的 f[][]就是前缀和数组，在计算f[i][j]的方案数的时候可以 $O(1)$得到,因此只需要额外开一个数组f，因为每次计算的时候都是用前面计算过的
其实这里可以完美的用闫式dp分析得出，看下图

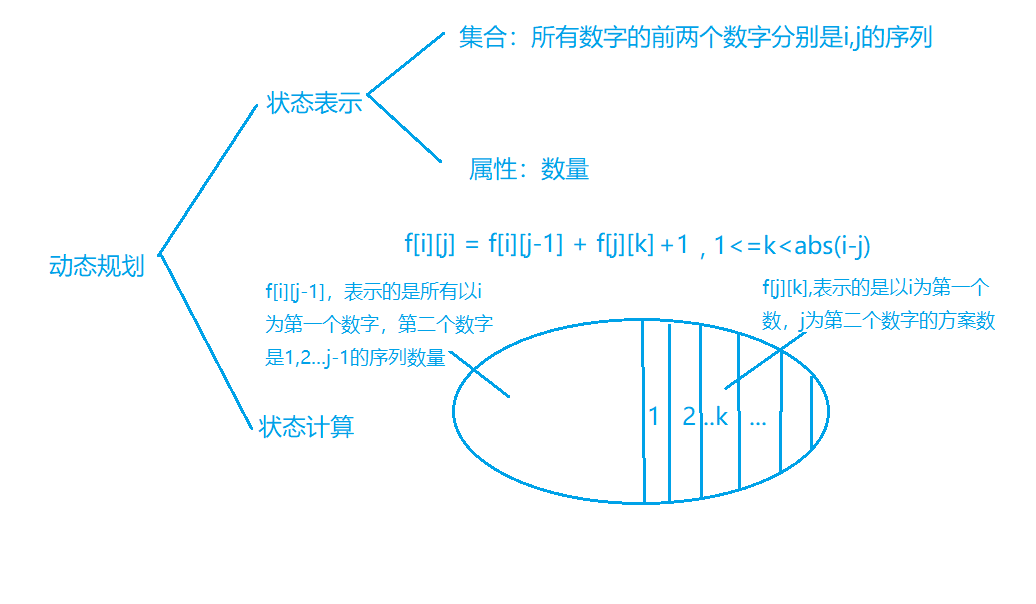
状态转移方程中由于当前序列[i,j]也是个合法序列，要加上1

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>


using namespace std ;

const int N = 1010,P = 10000 ;

int f[N][N] ;
int n ;

int dfs(int last,int cur){
    if(f[last][cur] != -1) return f[last][cur] ;
    if(cur<=0) return 0 ;//不合法序列
    return f[last][cur] = (1 + dfs(last,cur-1) + dfs(cur,abs(last-cur)-1)) % P ;
}

int main(){
    scanf("%d",&n) ;

    memset(f,-1,sizeof f) ;
    dfs(n,n) ;

    printf("%d\n",f[n][n]) ;

    return 0 ;

}

这篇博客记录了一道题目从50分到100分的过程，感受到了所有代码的优化都是一点点来的
由于整理的匆忙，文中不对的地方，请各位大佬一一指正
在文章的最后要感谢各路大佬的悉心帮助和教导，一并感谢
小呆呆 九歌
胡图图
墨姐姐 对称美
wzc1995