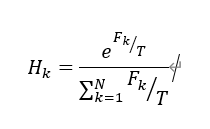算法原理

在生物进化过程中，大都会经历繁殖、交叉、变异和选择四个基本阶段。繁殖生物都有的基本现象，每个个体都是其上一
代经过繁殖所得来。通过繁殖，子代和亲代能够保证生物性状的相似性。而有性繁殖是被证明最有利于进化的繁殖方式。
生物在有性繁殖下一代时，两个同源染色体利用交叉而重新组合产生新染色体，即两个染色体进行某些部分进行互换。变
异是染色体上某些基因发生突变现象。选择就是适应环境的物种会生存下来，而不适应环境的物种就会被2淘汰，即“适者
生存，优胜劣汰”。

算法模型

遗传算法需要通过编码实现对个体的表示，并利用适应度函数对个体优劣进行评价，还要通过选择、交叉、和变异等进化
操作实现优化搜索。



1. 编码方式
  遗传算法的编码方式有：二进制编码、自然数编码、实数编码和树形编码。其中最常见的是二进制编码。

2. 适应度函数
    在遗传算法中，每个个体都有一个适应度函数值相对应。其优劣需要通过适应度函数值大小进行定量评价。个体越优，
    其适应度函数值越大。适应度函数值是执行“适者生存，优胜劣汰”的依据，直接决定搜索群体的进化行为。
    最大值优化问题：G(x) = max g(x)
                    F(x) = G(x) + Cmin if G(x) + Cmin > 0 else 0 (Cmin是足够小的数)
    最小值优化问题：G(x) = min g(x)
                    F(x) = Cmax - G(x) if G(x) - Cmin > 0 else 0 (Cmax是足够大的数)

3. 选择操作
    选择就是从当前群体中选择适应度函数值较大的个体，使这些优良个体有可能作为父代来繁殖下一代。在该阶段，
    个体的适应度函数值越大，被选择作为父代的概率越大，个体的适应度函数值越小，被淘汰的概率越大。
    轮赌盘算法:
        计算每个个体被选择进入下一轮的概率，即Pi = $\frac{Fi}{ \sum_{i=1}^nFi}$
        根据选择概率Pi将圆形赌轮分成n份，转动轮盘一次，假设参考点落入第i个扇形中，就选择第i个个体。

4. 交叉操作
    在遗传算法中，交叉是产生新解的重要操作。要进行交叉，首先需要解决配对问题，采用随机配对是最基本的方法
    。一般情况下，二进制编码的个体采用点交叉方法。所谓点交叉就是在两个配对字符串随机选择一个或者多个交叉
    点，互换部分子串从而产生新的字符串。两个体是否进行交叉操作由交叉概率决定。较大的交叉概率可以使遗传算
    法产生更多的新解，保持群体的多样性，并能防止算法早熟。但是交叉概率过大，会使算法过多搜索不必要的解区
    域，消耗过多的计算时间，通常情况下，交叉概率取值0.9左右。

5. 变异操作
    在遗传算法中，变异是产生新解的另一种操作。交叉操作相当于进行全局探索，而变异操作相当于进行局部开发。
    而全局搜索和局部开发都是智能优化算法必备的两种搜索能力。对二进制染色体进行变异操作，等价于进行补运算
    ，即将字符0变为1，字符1变为0。个体是否进行变异操作由变异概率决定。变异概率过低，部分有用的基因就难以
    进入染色体，不能有效提升算法解的质量；变异概率过强，子代容易丧失父代优良的基因，导致算法失去搜索经验
    进行的学习的能力。一般情况下，变异概率的取值为0.005左右。

算法的步骤：

(1) 产生初始群种。
(2) 计算每个个体适应度函数值。
(3) 利用轮盘赌算法选择进入下一代群体中的个体。
(4) 两两配对的个体进行交叉操作以产生新个体。
(5) 新个体进行变异操作。
(6) 将新个体中迄今出现的最好个体直接复制到下一代中(精英保留策略)。
(7) 反复执行(2)到(6)直到满足算法终止条件。

算法分析

一个好的智能优化算法，其关键在于全局探索和局部开发能力的平衡。全局探索的主要目的是对解空间进行更全面的搜
索，希望发现更多的未知区域；而局部开发主要目的是对已知区域进行更为精细的搜索，希望获得质量更好的新解。对
遗传算法而言，可以通过设置选择压力来实现全局探索和局部开发能力的平衡。所谓的选择压力，是指选择机制给适应
度值低个体造成的生存压力平衡。过大的选择压力，会使得群体中适应度值低的个体快速被淘汰，降低了群体的多样性
，从而使得算法的搜索空间急剧减少；过小的选择压力，会使得适应度值大的选择个体不容易产生更多的后代，从而使
得算法的优化速度大幅度下降。因此，在算法运行的初始阶段，设置较小的选择压力可以使算法具有较好的全局探索能
力，能够进行全面的广域搜索；在算法后期，设置较大的选择压力使得算法具有较好的局部开发能力，能够对已有区域
进行比较精细的局部搜索。对选择压力的设置，可以从两方面进行分析：适应度函数标定以及选择策略。
1. 适应度函数标定
    一般情况下，在遗传算法的初始阶段，搜索个体的适应度函数值差异显著。极少数高适应度值个体会被多次选择，
    低适应度值个体，尽管自身携带有效基因，也会被过早淘汰。在这种情况下，群体多样性较差，算法容易早熟收敛
    。此时，应该缩小个体之间适应度的差距。而在算法运行的最后阶段，各个个体的适应度值差别较小。此时，应该
    扩大个之间适应度值的差距，保证算法能够在高适应度个体对应解区域进行集中搜索，加快算法收敛速度。
    (F:变换前的适应度函数；H：变换后的适应度函数;avg(F)：变换前F的平均值)
    1) 线性尺度变换法: H = aF + b (a, b根据具体问题设置)
    2) σ截断法: H = F + (avg(F) - cσ) (c根据具体问题设置)
    3) 幂律尺度变换: H = F^α (α > 1, 选择压力增加； α < 1, 选择压力减少)
2. 选择策略
    在遗传算法中，一方面要保持搜索群体的多样性，设置低选择压力可选择多种类型的个体，加强对未知解区域的搜
    索，避免算法陷入局部极值，但算法优化速度变得缓慢；另一方面要设置高选择压力可选择优良个体，实现优胜劣
    汰，可以加速优化速度但群体多样性会下降，会减小搜索到全局最优值的概率。目前，可以通过选择策略调节选择
    压力和群体多样性之间的矛盾。除了之前介绍的轮盘赌算法，选择策略还有分级选择法、锦标赛选择法和Boltzman
    n。
    1) 分级选择法:假设群体规模为N，所有个体按适应度排名依次记为1，2...i...N。排名为i的个体被选择概率记为
    prob(i)
    prob(i) = q - (i - 1)d (线性) or prob(i) = q(1 - q)^(i - 1) (非线性)

$\sum_{i=1}^Nprob(i)=1$
2)锦标赛选择法：这种选择策略也基于排名的思想，但不进行显示排名。在当前群体中，每次随机选择k个个体，
然后从这k个个体中选出适应度值最大的个体进入到下一代群体中。被选择的个体仍然返回当前群体中，参加下一
次k个个的随机选择。重复上述过程N次，就可以产生N个个体，达到群体规模要求。

    3) Boltzmann 选择法:参考模拟退火法，通过控制温度来调节压力。

其中Hk表示第k个个体转换后的适应度的值；Fk表示第k个个体转换前适应度的值；T为控制温度，随迭代次数而逐步降低