二分

lower_bound 较低边界

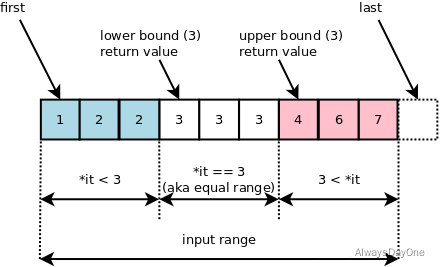
返回指向范围 [first, last) 中首个不小于（即大于或等于） value 的元素的迭代器，或若找不到这种元素则返回 last 。

范围 [first, last) 必须已相对于表达式 element < value 或 comp(element, value) 划分，即所有令该表达式为 true 的元素必须前趋所有令该表达式为 false 的元素。完全排序的范围满足此判别标准。

第一版本用 operator< 比较元素，第二版本用给定的比较函数 comp 。

upper_bound 较高边界

返回指向范围 [first, last) 中首个大于 value 的元素的迭代器，或若找不到这种元素则返回 last 。采用二分实现，所以调用前必须保证有序。

范围 [first, last) 必须已相对于表达式 !(value < element) 或 !comp(value, element) 划分，即所有令此表达式为 true 的元素必须前趋所有令此表达式为 false 的元素。完全排序的范围满足此判别标准。

第一版本用 operator< 比较元素，第二版本用给定的比较函数 comp 。

lower_bound 返回数组中第一个不小于目标值的元素的iterator，（第一个>=target的数）

upper_bound 返回数组中第一个大于目标值的元素的iterator， （第一个>target的数）

前缀和 差分

b :     1  1 -1  2 -1
a :     1  2  1  3  2
s :  0  1  3  4  7  9

fun: B 差分函数 S 前缀和函数
b = B(a)
s = S(a)
a = S(b)
a = B(s)
a = S(B(a))
a = B(S(a))

• 数组不变，区间查询：前缀和、树状数组、线段树；

• 数组单点修改，区间查询：树状数组、线段树；

• 数组区间修改，单点查询：差分、线段树；

• 数组区间修改，区间查询：线段树。

int 溢出

long long res = int * int;
int * int 即使结果是long long 也会溢出，需要把其中一个强制转换成long long
res = (long long)int * int; res = int * (long long)int; res = int * 8ll;

坐标系

在数学中，坐标系有以下种，一是平面直角坐标系，二则是平面极坐标系，三是柱坐标系，四是球坐标系

数组坐标系 = 直角坐标系 + 90度
二维数组与坐标
二维数组的[0][1] 不是 平面直角坐标系中的（0,1），而是（1,0）。
也就是说，在二维数组中，第一个数对应的其实是纵坐标，第二个数对应的其实是横坐标。

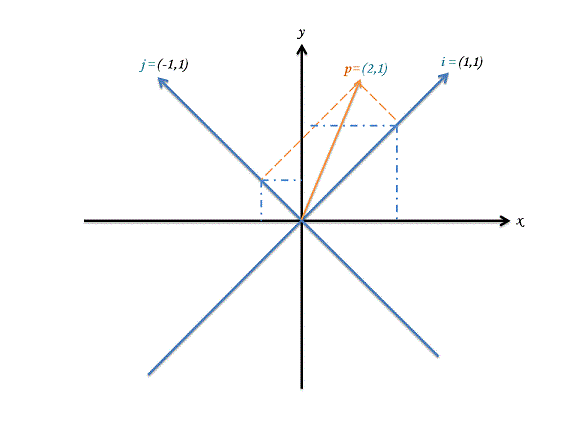
用两维的笛卡尔坐标系表示的二维空间

AC Terminal

复制 ctrl + insert
粘贴 shift + insert
单选 双击
多选 shift + 单击 + 移动鼠标

C++编译时开启O2优化

O1优化会消耗少多的编译时间，它主要对代码的分支，常量以及表达式等进行优化。
O2会尝试更多的寄存器级的优化以及指令级的优化，它会在编译期间占用更多的内存和编译时间。
O3在O2的基础上进行更多的优化，例如使用伪寄存器网络，普通函数的内联，以及针对循环的更多优化。

#pragma GCC optimize(2)
#pragma GCC optimize(3)

swap 使用异或运算交换两个变量的值

2009年7月14日, Hallvard Furuseth 建议在一些机器上 (((a) ^ (b)) && ((b) ^= (a) ^= (b), (a) ^= (b))) 可能会更高效，由于 (a) ^ (b) 表达式会被复用。

#define SWAP(a, b) (((a) ^= (b)), ((b) ^= (a)), ((a) ^= (b)))

max min

#define max(a,b) (((a) > (b)) ? (a) : (b))
#define min(a,b) (((a) < (b)) ? (a) : (b))

GCC编译器内置宏定义

-E 预处理后即停止，不进行编译。预处理后的代码送往标准输出
-dM 告诉预处理器输出有效的宏定义列表

gcc -E -dM - </dev/null

函数比较

1 阶乘函数阶乘是比指数函数快的函数中增长最慢的。因为指数函数的增长一直都是以底数的倍数，而阶乘函数的增长是以自然数列为倍数。0！=1,1！=1,2！=2,3！=6,……n！=n(n-1)！必有3x！>2^x。
2 幂指函数幂指函数就是y=x^x，增长稍快于阶乘，阶乘要从1出发，而幂指直接以底的底次方增长，显然快于阶乘函数。但是3x！>x^x，而x^x>x！
3 幂函数指数函数指y=x^x^n，增长比幂指函数快，其中指数以幂函数的速度增长，而指数函数的指数只是以自然数列增长，说明该函数增长比幂函数快的多。上面那三个增长率还是菜鸟，还是看下面的。
4 超乘方函数指的是y=x↑↑n，也就是y=x^x^x^x^……^x(n个x相乘方)，其增长速度比幂函数指数函数快。当n=4,x>3时，该函数值用计算机算不出来。
5 超指数函数指的是y=a↑↑x(a>=2)，x=2时。y=a^a,x=3时，y=a^a^a,以此下去，超指数函数速度比超乘方要快，y=2↑↑x,x>6,计算机算不出来，而且2↑↑6>1000↑↑3。
6 阶幂函数。n！(上标)=n^(n-1)^(n-2)^……^2^1，n！=n^(n-1)！阶幂函数的增长率实际上跟超指数是一个等级。但是3↑↑x已经可以盖往阶幂，而2↑↑x比不过阶幂。
7 阿克曼函数和高德纳函数。阿克曼函数就是A(m,n)，增长率高，A(4,3)计算机算不出来，实际上阿克曼函数A(m,n)=2(第m级运算)(n+3)-3=2↑(m-2)(n+3)-3，当然，A(a,x)的增长率显然远远不及A(x,a)。另外，高德纳函数就是指类似y=a↑xb(a,b∈N+,a,b>=2,a,b不能同时=2)的函数，其中y=2↑x3的增长率远远比指数快。x>4时那部分的图像犹如垂线。y=2时,x=16,y=3,x=65536,y=4,x=2↑↑65536,y=5,x=2↑↑↑(2↑↑65536)……是增长非常快的函数。高德纳函数跟阿克曼函数并列是他们俩增长率相当。
8 葛立恒函数葛立恒函数增长率比阿克曼函数要快的多。葛立恒函数就是y=gx，其中x=0时，y=4,(g1=3↑↑↑↑3，所以g0=4),然后x=1,y=3↑↑↑↑3,x=2,y=3↑(g1)3，……x=n，y=3↑(gn-1)3,比阿克曼函数要快的多，g1相当于A(6,1)，而g2相当于A(A(6,1),1),g3=A(A(A(6,1),1),1)……显然阿克曼函数增长率不如葛立恒函数。x=64时，y=葛立恒数。此时阿克曼函数的迭代有64次。
9 四段康威链。y=a→b→x→c，或者y=a→b→c→x(a,b>2,且a,b不能同时=2)。前者增长率远不及后者，y=2→3→x→2和y=2→3→2→x增长率是不同一个等级。后者x=4时，前者的括号要七层才能表示出来。前者x=65时，大约相当于葛立恒数。但增长跟葛立恒函数一样，而后者增长率远远超过葛立恒函数，2→3→2→5用葛立恒函数表示不出来。
10 cg函数cg函数是康威链的高级运算。cgn=n→n→n→……→n(n个n)，y=cgx，x>4时就已经超过葛立恒数，而x>5时四段康威链表示不出来。指数函数在cg函数面前简直就跟对数和反阿克曼函数一样。
11 C函数C(n)=a→aa(左边的a为下标)a→b+c=a→ba→ba→ba→……→ba(c个箭头)其中C3=3→33=3→23→23→23=3→23→2(3→22→2(3→22→23)→22)→22=……其中3→22→23=3→2(3→21→23)→22=3→23→22=3→2(3→22→22)=3→2(3→2(3→21→22))=3→2(3→23)=3→2(3→3→3→3)为3→3→3→3个3进行康威链。因此C3用普通的康威链无法表示出来，C4不用说，但c函数可以为一元，二元，三元函数。c(x,x,x),当x=1,y=1,x=2,y=4,x=3,y=超级大数。这个函数增长率直接吊打阿克曼，阿克曼函数在它面前做对数函数的份也没有。
12 Circle函数Circle函数增长率比C函数快，Circle10用C函数表示不出来，不过Circle4，Circle5还可以用C函数限制范围。
13 ＃。类似y=x＃＃……＃＃x的函数。五个＃就能完爆Circle函数，六个＃，七个＃可想而知他增长有多快了。如果还有个y=100＃x100，当x=n时，＃就有n个，那增长就更快了。
14 TREE函数当然，后面的函数下一个比上一个快，这时应该就是TREE函数了，TREE1,TREE2,都只是一位数，而TREE3是一个多人皆知的超级大数，TREE3用康威链和康威链下标表示不出来。康威链在TREE函数面前，增长的速度可就跟对数函数没啥区别。更不用提那什么指数，在TREE面前它就是一个常值函数一样。根本没什么增长率。
15 SSCG函数SSCG的增长比TREE要强多，TREE3迭代TREE3次跟SSCG3相比，和0没什么区别。而TREE2只是一位数，由此而知SSCG增长是多么的快了。阿克曼函数在SSCG函数就像是一个常值函数，连做对数函数的份也没有了。SSCG4,SSCG5等等你可以自行想象他有多大。
16 Rayo函数这个才是主角，Rayo函数虽然要在10^100这么大才能是个大数，但是这个大数，即使SSCG3用SSCG迭代SSCG3次整体再SSCG3次，跟Rayo10^100相比，就和0是一个道理。而Rayo10^100就能给所有能算的有限数定上下限了。当然，这只是其中比较常见的，当然，比指数增长快的，不仅仅是只是以上这17个函数，当然，你还可以创造y=2↑↑↑x,y=3↑↑↑x等等函数，这也是比指数函数快的。不过，以上的函数趋于无穷的基数不同，前面的阶乘，幂指，幂函数指数趋于阿列夫一，当然，指数也是趋于阿列夫一。而超乘方趋于阿列夫n，超指数，阶幂趋于阿列夫阿列夫零，而阿克曼和高德纳，趋于的是阿列夫零→阿列夫零→阿列夫零，后面的函数的无穷比前面的要高。