0. 序言
昨天看 y总的 next 数组值的定义和我所学的 next 数组值的定义有所不同,看起来大体相同,但 next[2]值的想法却不一样,
举个例子:
| 字符串 | a | b | a | b | a | c |
|---|---|---|---|---|---|---|
| 下标 | 1 | 2 | 3 | 4 | 5 | 6 |
| y总 | 0 | 0 | 1 | 2 | 3 | 0 |
| 课本里 | 0 | 1 | 1 | 2 | 3 | 4 |
经过一番思考 , 我得出了答案,下文会给出 next 数组的定义和推导方法,以及课本和y总的不同点在哪里。
PS:
- 本文 next 数组下标一律从1开始,next[1] = 0,用0表示不匹配。
- 网上还有一些 next数组是从下标0开始,next[0] = -1 ,用 0 或者 -1 表示不匹配, 但与本文所提的两种方式逻辑是一样的。
1. next 数组的定义
KMP 的 next 数组简单来说,假设有两个字符串,
一个是待匹配的字符串 S ,
一个是要查找的模式串 P。
现在我们要在 S 中去查找是否包含 P,
用 i 来表示 S 遍历到了哪个字符 ,
用 j 来表示 P 匹配到了哪个字符。
如果是暴力的查找方法,当 S[i]和 P[j] 匹配失败的时候,i 和 j 都要回退,然后从 i-j+1 的下一个字符开始重新匹配。
而 KMP 就是保证 i 永远不回退,只回退 j 来使得匹配效率有所提升。它用的方法就是利用 P 在失配的 j 为之前的成功匹配的子串的特征来寻找 j 应该回退的位置。而这个子串的特征就是前后缀的相同程度。 即充分利用已知信息
所以 next 数组其实就是查找 P 中每一位前面的子串的前后缀有多少位匹配,从而决定 j 失配时应该回退到哪个位置。
拿的J大佬的过程图,过几天自己画一个
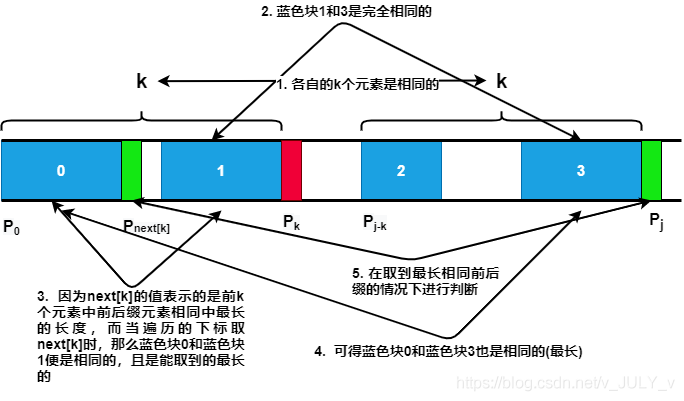
2. 两种版本 next 数组值推导
2.1 根据最大公共元素求 next 数组
2.1.1 基本概念
- 前缀:包含首位字符但不包含末位字符的子串。
- 后缀:包含末位字符但不包含首位字符的子串。
- 最大公共子串长度:也就是前缀和后缀拥有的相同子串的最大长度。
- next[j]:其值 = 第
j位字符组成的子串的最大公共子串长度
以 abab 为例

则 y总版 next 数组可以得到如下:
| 字符串 | a | b | a | b | a | c |
|---|---|---|---|---|---|---|
| 下标 | 1 | 2 | 3 | 4 | 5 | 6 |
| next[j] | 0 | 0 | 1 | 2 | 3 | 0 |
2.1.2 以 j+1 位匹配字符串的版本 (y总版)
所谓以 j+1 位相匹配字符串版本,就是 第 i 位 与 第 j+1 位匹配,看是否成功
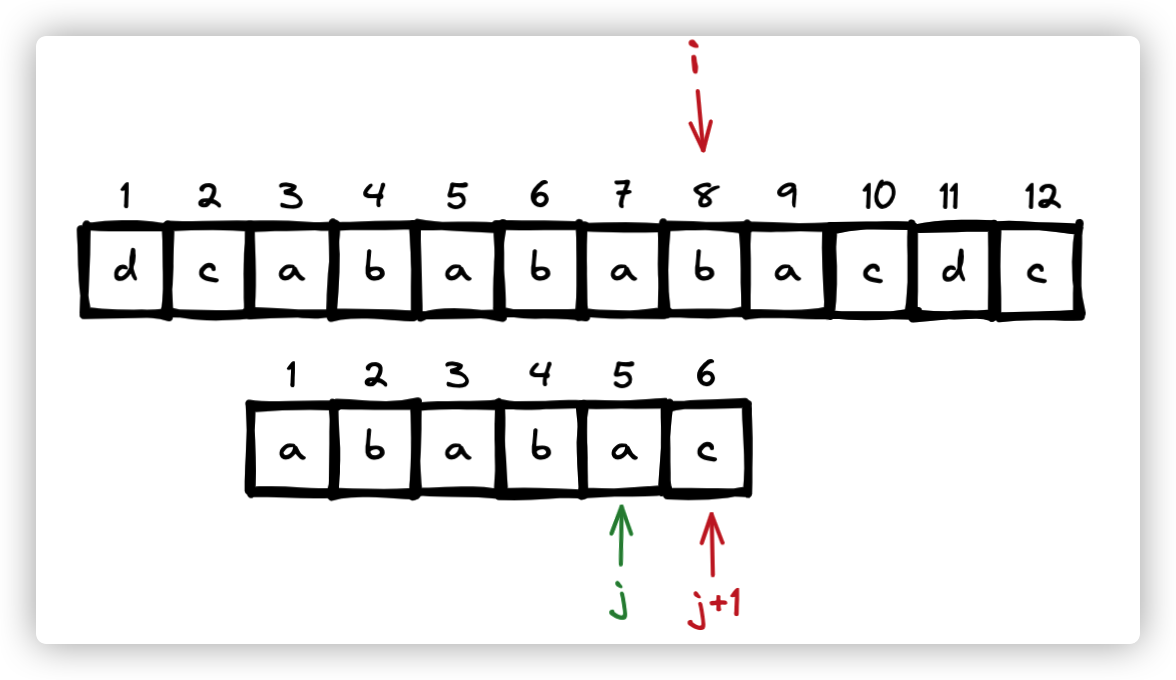
当 p[j+1] != s[i] 的时候, j = next[j] 此时 从j = 5 变成了 j = 3,相当于字符串右移两位。
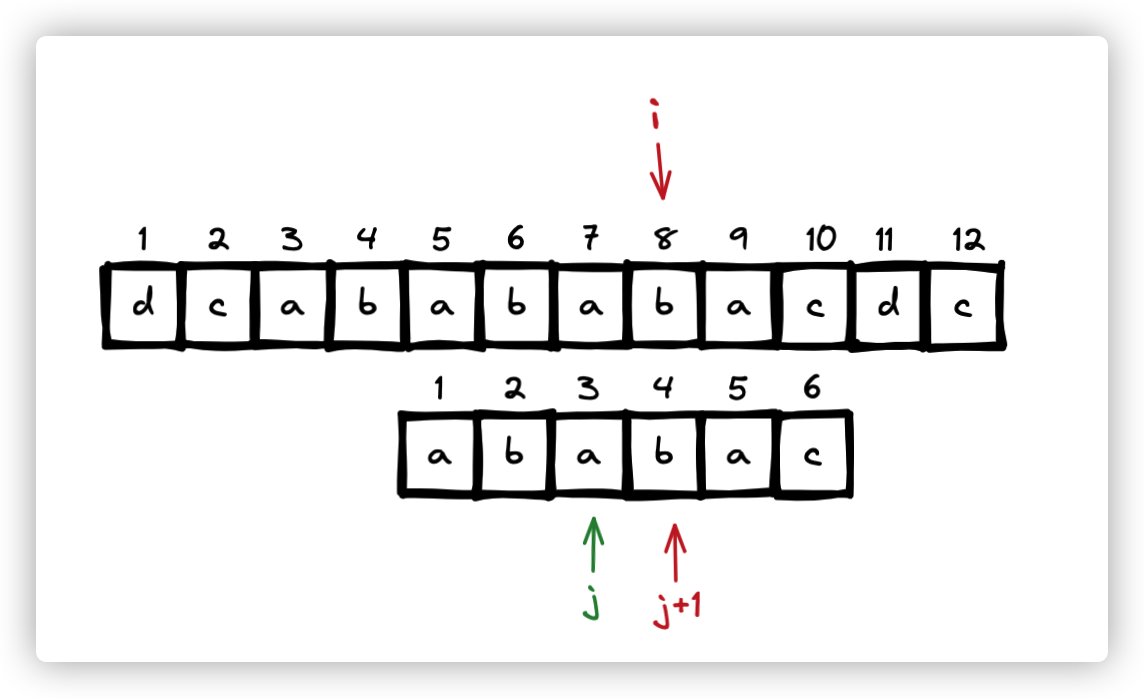
此时 p[j+1] == s[i] , 则 j++; i++ 直至匹配成功
2.1.3 以 j 位匹配字符串版 (大部分书籍里的版本)
大部分教科书里的版本是以第j位匹配字符串的,如:《大话数据结构》、《严版数据结构》 、《算法 第四版》、《维基百科版》,以及网上next[0] = -1版,都是用第j位去匹配字符串第i位的。
现在我来说说这种版本与 y总版的设定相同之处与不同之处。
- 与上文的基本概览的四个条件相比,前三个条件相同,第四个条件不同
- 前缀:包含首位字符但不包含末位字符的子串。
- 后缀:包含末位字符但不包含首位字符的子串。
- 最大公共子串长度:也就是前缀和后缀拥有的相同子串的最大长度。
- next[j]:其值 = 第
j位字符前面j-1位字符组成的子串的最大公共子串长度+1。
故可得
| 字符串 | a | b | a | b | a | c |
|---|---|---|---|---|---|---|
| 下标 | 1 | 2 | 3 | 4 | 5 | 6 |
| next[j] | 0 | 1 | 1 | 2 | 3 | 4 |
第j为匹配字符串,如图
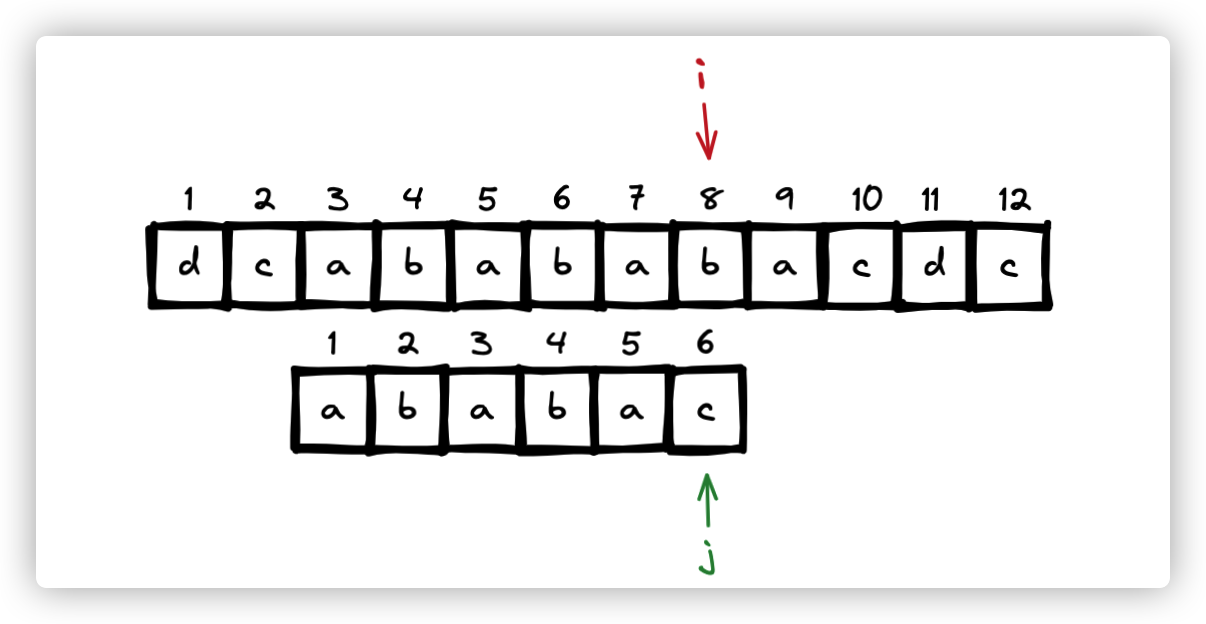
当 s[i] != p[j] 时 , j = next[j] 此时,从 j = 6 变成了 j = 4 ,字符串也右移了两位。
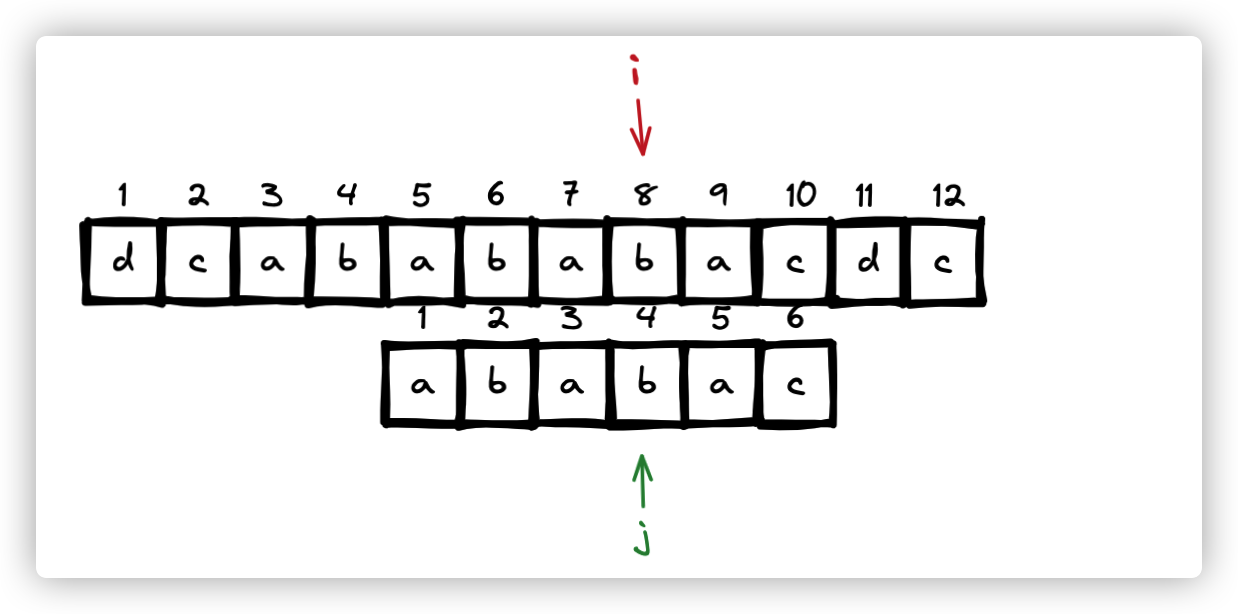
此时s[i] == p[j] ,则 i++,j++ , 直至匹配成功。
2.1.4 两个版本的总结,以及第三版本的诞生
- 两个版本的
next数组求值,总结如图

相信大家也看出来了,y总与教科书版的不同之处只在于与i相匹配的是j+1还是j。
字符串的移动次数都是j - next[j]
其思想都是利用next数组减少指针回溯。
那如果,我们一定要用 y总的版本的 j 指针去匹配字符串i指针,而不是用j+1的话,
那是否可行呢?如果可行那该怎么操作呢?
答案:是可行的!
该怎么操作之前,得说两点很容易得出的结论。
1. next[j+1] 的最大值 = next[j] + 1
2. 模式串最后一位不管是什么字符都不影响整个KMP算法的匹配也即是 j = next[j] (自己想想很容易得出来)
所以呢,我们可以让next数组的值先加 1 再右移 1 位,第 1 位补0。
| 字符串 | a | b | a | b | a | c |
|---|---|---|---|---|---|---|
| 下标 | 1 | 2 | 3 | 4 | 5 | 6 |
| next[j]pre | 0 | 0 | 1 | 2 | 3 | 0 |
| next[j]aft | 0 | 1 | 1 | 2 | 3 | 4 |
这样做的目的是让现在的字符串移动的次数和原来字符串移动的次数保持不变。
即j - next[j] == 原来的j - next[原来的j]
这样就不会影响整个KMP算法流程。
聪明的小伙伴们可能发现了,这不就是教科书版的next数组吗。
没错,这就是教科书版的next数组。
至于为什么有这么多版本的next数组,我认为是KMP算法的思想被各个大佬所学习,各个大佬对next数组有自己的理解,他们根据自己的理解诞生了不同的next数组求法,但思想是一致的。
- 下面说说第三种版本
那么聪明的小伙伴们可能就明白了,既然我可以把next数组右移匹配j+1 , 那我为什么不把模式串左移让j+1指向以前的j啊。
2.1.5 第三个版本的next数组
没错,我们把模式串左移1位,(因为next数组和字符串从下标1开始,所以我们左移1位是可行的)。
那我们左移操作要把next值减1吗?
因为字符串移动次数是j - next[j] , 而左移1位后下标从0开始 , 故要保持移动次数不变的话,next数组值不变且位置不变。
| 字符串 | a | b | a | b | a | c |
|---|---|---|---|---|---|---|
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 |
| next[j] | x | 0 | 0 | 1 | 2 | 3 |
此时要让next[0]成为辨别匹配失败的标志, 如果x = -1 , 即 next[0] = -1 的话,
(ΩДΩ) 那么第三个版本的next数组不就出来了,也就是网上流行的另一种版本。
| 字符串 | a | b | a | b | a | c |
|---|---|---|---|---|---|---|
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 |
| next[j] | -1 | 0 | 0 | 1 | 2 | 3 |

至此,所有出现在市面上的next数组求法都被我们所了解啦。
2.2 数学归纳法求next数组
这个不用看,就是把代码的思路写出来了
- 初始条件: 字符串长度
len > 2,下标从1开始,next[1] = 0 , next[2] = 1;i = 3 - 假设第
i位之前的next[1 ~ i - 1]值已知 -
开始推导 第
i个位置的next[i]值 -
if(p[i-1]== p[next[i-1]]) (即这两个值是否相等)第 i 个位置的前一个位置的值(即 p[i-1])与以该位置的next 值(即 next[i-1])为下标的值(即 p[next[i-1]])是否相等
若相等,则
next[i] = next[i-1] + 1
若不等,则继续往回找,检查
- if(p[i-1]== p[next[next[i-1]]])
若相等,则 `next[i] = next[next[i-1]] + 1`
若不等,则继续往回找,直到找到下标为 1 还不等(即字符串第一个元素),直接赋值 next[i] = 1
3. 写代码
首先,无论是哪种版本的 next 数组,写出来的代码都是数学归纳法的思想。
数学归纳法的三个步骤:
1. 确定初始条件
2. 假设条件在 x 范围内成立
3. 推导是否在 x+1 成立
用数学归纳法推导next 数组值的三个步骤:
1. 确定初始状态 next[1] = 0 ; j = 0
2. 假设第 i 位之前的 next[1~i - 1] 值已知,现求 next[i]
3. 匹配 p[i] == p[j] ? next[i] = ++j : j = next[j]
3.1 y总版
next数组的求法- 初始状态
next[1] = j = 0, 假设next[1~ i - 1]已求出,目标求解next[i] - 不断扩展匹配长度
j,如果扩展失败(下一个字符不相等),则j = next[j],直至j为0(就重头开始匹配) - 如果匹配成功,匹配长度
j就自增1 ,next[i] = j
//初始化条件
next[1] = 0;
// 根据上面所说,y总版 j 表示匹配成功长度,初始化为0,下标从 1 开始,故 i = 2, 因为 j + 1 与 i 匹配,且 next[1]已被初始化
for(int i = 2, j = 0 ; i <= n ; i++)
{
//匹配失败, j = next[j]
while(j>0&&p[i]!=p[j+1]) j = next[j];
//匹配成功,j++
if(p[i] == p[j+1]) j++;
//记录此时j的长度
next[i] = j;
}
- KMP匹配算法
- 因为定义的相似性,求解字符串匹配与求解next数组过程基本是一致的
// 从 j+1 开始匹配 所以 j = 0 , 下标从1开始, 所以 i = 1
for(int i = 1 , j = 0 ; i <= m ; i++)
{
//匹配失败, j = next[j]
while(j > 0&&s[i]!=p[j+1]) j = next[j];
//匹配成功,j++,i++匹配下一个字符串
if(s[i] == p[j+1]) j++;
//j == n 完全匹配成功
if(j == n)
{
cout << i - j << " ";
//继续匹配,保证所有字符串全部匹配
j = next[j];
}
}
画了个流程图帮助理解
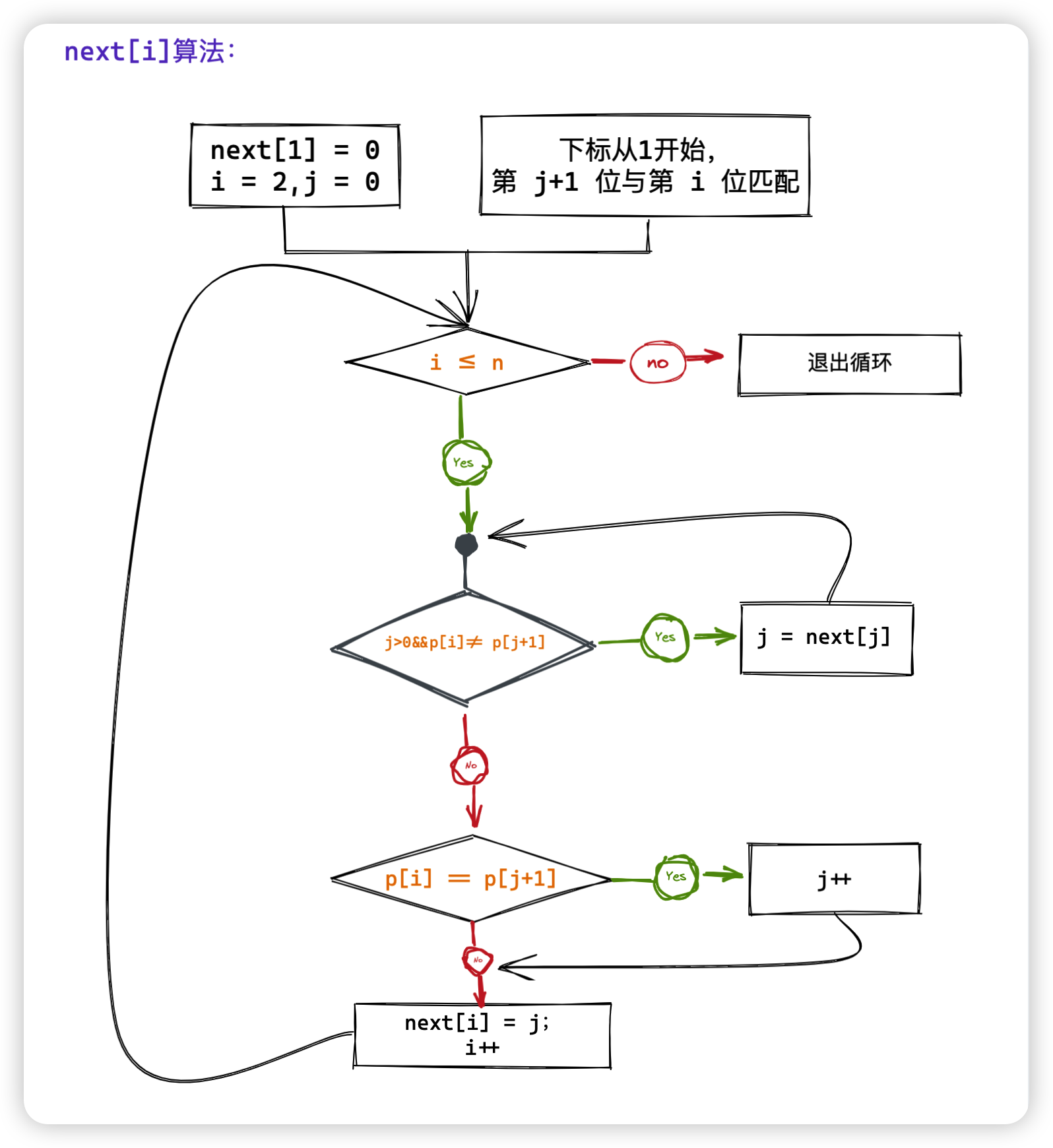
3.2 教科书版 (第 j 位匹配版)
- next数组的求法
- 与上面类似,只是从第 j 位开始匹配,记录的是 匹配成功长度+1
next[1] = 0;
//依然 用next[1] = 0表示匹配不成功
int i = 1 , j = 0;
while(i < n)
{
if(j == 0 || p[i] == p[j])
{
next[++i] = ++j;
}
else
j = next[j];
}
- KMP算法
void KMP()
{
int i = 1 , j = 1;
while(i <= m && )
{
if(j == 0 || s[i] == p[j])
{
i++;
j++;
}
else
j = next1[j];
if(j > n)
{
printf("%d ",i - j);
j = next[j];
}
}
}
最后
码了几个小时的字和画图,大家点点赞吧。


教科书版的过不了(
%%%%%%,很不错的题解,清楚的解释了每个版本next数组不同的原因和如何转化。
有个小问题可以修改一下,因为第一次看的时候没看懂它所代表的意思
2.1.4 及以下部分的next数组没做版本区分,所导致的不能理解等式的含义
即 next[j+1] = next[j] +1
应标注版本,且 j 的含义不同也需要区分一下。
我看了好几遍才理解。